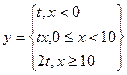Задача 2.3. Клавиши курсора

Написать программу, определяющую, какая из курсорных клавиш была нажата.

 

В составе библиотеки, унаследованной от языка С, есть функция getch (), возвращающая код нажатой пользователем клавиши. В случае нажатия функциональных или курсорных клавиш эта функция возвращает 0 либо ОхЕО (в зависимости от компилятора), а ее повторный вызов позволяет получить расширенный код клавиши.

 

#include < stdio.h> #include < conio.h> int main () { int key; printf (" \n Нажмите одну из курсорных клавиш: \n"); key = getch (); key = getch (); switch (key) { case 77: printf (" стрелка вправо\n"); break; case 75: printf (" стрелка влево\n"); break; case 71: printf (" стрелка вверх\n"); break; case 80: printf (" стрелка вниз\n"); break; default: printf (" не стрелка\n"); } return 0; }

 

Выражение, стоящее в скобках после ключевого слова switch, а также константные выражения в case должны быть целочисленного типа (они неявно приводятся типу выражения в скобках). Если требуется выполнить одни и те же действия при нескольких различных значениях констант, метки перечисляются одна за другой, например:

 

case 77: case 75: case 72: case 80: printf (" стрелки"): break;

 

Метки сами по себе не вызывают изменения порядка выполнения операторов, поэтому если вы не хотите, чтобы управление было автоматически передано на первый оператор следующей ветви, необходимо после каждой ветви использовать оператор break.

 

СОВЕТ

Хотя наличие слова default и не обязательно, рекомендуется всегда обрабатывать случай, когда значение выражения не совпадает ни с одной из констант. Это облегчает поиск ошибок при отладке программы.

 

Оператор switch предпочтительнее оператора if в тех случаях, если в программе требуется разветвить вычисления на количество направлений, большее двух, и выражение, по значению которого производится переход на ту или иную ветвь, является целочисленным. Часто это справедливо даже для двух ветвей, поскольку улучшает наглядность программы.

 

Циклы

 

Теоретический материал: с. 44-49, 237.

 

Цикл — участок программы, повторяемый многократно. В C++ три взаимозаменяемых оператора цикла - while, do while и for. При написании любого цикла надо иметь в виду, что в нем всегда явно или неявно присутствуют четыре элемента: начальные установки, тело цикла, модификация параметра цикла и проверка условия продолжения цикла (рис. 2.4). Начинающие чаще всего забывают про первое и/или третье.

 

Рис. 2.4. Блок схема цикла.

Задача 2.4. Таблица значений функции

Написать программу печати таблицы значений функции

для аргумента, изменяющегося в заданных пределах с заданным шагом. Если t > 100, должны выводиться целые значения функции.

 

Исходными данными являются начальное значение аргумента Хn, конечное значение аргумента Хk, шаг изменения аргумента dX и параметр t. Все величины — вещественные. Программа должна выводить таблицу, состоящую из двух столбцов — значений аргумента и соответствующих им значений функции.

 

В словесной форме алгоритм можно сформулировать так:

1. Ввести исходные данные.
2. Взять первое из значений аргумента.
3. Определить, какому из интервалов оно принадлежит.
4. Вычислить значение функции у по соответствующей формуле.
5. Если t > 100, преобразовать значение у в целое.
6. Вывести строку таблицы.
7. Перейти к следующему значению аргумента.
8. Если оно не превышает конечное значение, повторить шаги 3-7, иначе закончить выполнение.

 

В каждый момент времени требуется хранить одно значение функции, поэтому для него достаточно завести одну переменную вещественного типа. Шаги 3-7 повторяются многократно, поэтому для их выполнения надо организовать цикл. В приведенном ниже варианте используется цикл while:

 

#include < stdio.h> #include < math.h> int main () { double Xn, Xk, dX, t, y; printf (" Enter Xn, Xk, dX, t \n"); scanf (" %lf%lf%lf%lf", & Xn, & Xk, & dX, & t); printf (" ------------------------------------\n"); printf (" | X | Y |\n"); printf (" ------------------------------------\n"); double x = Xn; // Начальные установки while (x < = Xk) { if (x < 0) y = t; if (x > = 0 & & x < 10) y = t * x; if (x > = 10) y = 2 * t; if (t > 100) printf (" | %9.2lf | %9d |\n", x, (int)y); else printf (" | %9.2lf | %9.2lf |\n", x, y); x += dX; // Модификация параметра цикла } printf (" ------------------------------------\n"); return 0; }

Вот та же программа с использованием оператора for:

 

#include < stdio.h> #include < math.h> int main () { double Xn, Xk, dX, t, y; printf (" Enter Xn, Xk, dX, t \n"); scanf (" %lf%lf%lf%lf", & Xn, & Xk, & dX, & t); printf (" ------------------------------------\n"); printf (" | X | Y |\n"); printf (" ------------------------------------\n"); for (doube x = Xn; x < = Xk; x += dX) { if (x < 0) y = t; if (x > = 0 & & x < 10) y = t * x; if (x > = 10) y = 2 * t; if (t > 100) printf (" | %9.2lf | %9d |\n", x, (int)y); else printf (" | %9.2lf | %9.2lf |\n", x, y); } printf (" ------------------------------------\n"); return 0; }

В программу введена вспомогательная переменная х, которая последовательно принимает значения от Хn до Хk с шагом dX. Она определена непосредственно перед Использованием. Это является хорошим стилем, поскольку снижает вероятность ошибок (например, таких, как использование неинициализированной переменной).

 

СОВЕТ

В общем случае надо стремиться к минимизации области видимости переменных.

 

В первом варианте программы область видимости х простирается от точки описания до конца программы, во втором областью ее видимости является только цикл1, Что предпочтительнее, поскольку переменная х вне цикла не требуется. Вообще говоря, в условии цикла while допускается описывать и инициализировать переменную таким же образом, как в операторе if, но при этом синтаксис не допускает ее сравнения с Хk. Другим преимуществом второго варианта программы является то, что все управление циклом for сосредоточено в его заголовке. Это делает программу более читаемой.

 

Для преобразования значения функции к целому в программе использовалась конструкция (int)y, унаследованная из языка С. Строго говоря, в данном случае лучше применить операцию преобразования типа static_cast, введенную в C++2, но в старых компиляторах она может не поддерживаться:

 

printf (" |%9.2lf |%9d |\n", x, static_cast< int> (y));

 

Выполните программу несколько раз, задавая различные значения исходных данных. С помощью ручного просчета убедитесь в правильности вычислений. Рассмотрим теперь пример цикла, количество итераций которого заранее подсчитать невозможно3.

 

Задача 2.5. Вычисление суммы ряда!

 

Написать программу вычисления значения функции Ch x (гиперболический косинус) с помощью бесконечного ряда Тейлора с точностью ∈ по формуле:

 

 

Этот ряд сходится при | х | < ∞. Для достижения заданной точности требуется суммировать члены ряда, абсолютная величина которых больше ∈. Для сходящегося ряда модуль члена ряда С_n при увеличении п стремится к нулю. При некотором n неравенство |С_n| > ∈ перестает выполняться, и вычисления прекращаются.

 

Общий алгоритм решения этой задачи очевиден: требуется задать начальное значение суммы ряда, а затем многократно вычислять очередной член ряда и добавлять его к ранее найденной сумме. Вычисления заканчиваются, когда абсолютная величина очередного члена ряда станет меньше заданной точности.

 

До выполнения программы предсказать, сколько членов ряда потребуется просуммировать, невозможно. В цикле такого рода есть опасность, что он никогда не завершится — как из-за возможных ошибок в вычислениях, так и из-за ограниченной области сходимости ряда (данный ряд сходится на всей числовой оси, но существуют ряды Тейлора, которые сходятся только для определенного интервала значений аргумента). Поэтому для надежности программы необходимо предусмотреть аварийный выход из цикла с печатью предупреждающего сообщения по достижении некоторого максимально допустимого количества итераций.

 

Прямое вычисление члена ряда по приведенной выше общей формуле, когда x «водится в степень, вычисляется факториал, а затем числитель делится на знаменатель, имеет два недостатка, которые делают этот способ непригодным. Первый недостаток — большая погрешность вычислений. При возведении в степень и вычислении факториала можно получить очень большие числа, при делении которых друг на друга произойдет потеря точности, поскольку количество значащих цифр, хранимых в ячейке памяти, ограничено1. Второй недостаток связан с эффективностью вычислений: как легко заметить, при вычислении очередного члена ряда нам уже известен предыдущий, поэтому вычислять каждый член ряда «от печки» нерационально.

 

Для уменьшения количества выполняемых действий следует воспользоваться рекуррентной формулой получения последующего члена ряда через предыдущий Сn+1 = Cn х T, где Т — некоторый множитель. Подставив в эту формулу Сn и Сn+1, получим выражение для вычисления Т:

 

 

 

Ниже приведен текст программы с комментариями. Обратите внимание на заголовок цикла: в нем, кроме части начальных установок, заданы условие выхода из цикла и модификация параметра цикла, то есть в данной программе все составные части цикла присутствуют в явном виде.

 

#include < iostream.h> #include < math.h> int main () { const int MaxIter = 500; /* максимально допустимое количество итераций */ double x, eps; cout < < " \nВведите аргумент и точность: "; cin > > х > > eps; bool done = true; // признак достижения точности double ch = 1. у = ch; // первый член ряда и нач. значение суммы for (int n = 0; fabs(ch) > eps; n++) { ch *= x * x / ((2 * n + 1) * (2 * n + 2)); // очередной член ряда у += ch; // добавление члена ряда к сумме if (n > MaxIter){ cout «" \n Ряд расходится! "; done = false; break; } } if (done){ cout < < " \n Значение функции: " < < у < < " для х = " < < х < < endl; cout < < " вычислено после " < < n < < " итераций" < < endl; } return 0; }

 

Первый член ряда равен 1, поэтому чтобы при первом проходе цикла значение второго члена вычислялось правильно, n должно быть равно 0. Максимально допустимое количество итераций удобно задать с помощью именованной константы. Для аварийного выхода из цикла применяется оператор break (см. Учебник с. 50), который выполняет выход на первый после цикла оператор.

 

Поскольку выход как в случае аварийного, так и в случае нормального завершения цикла происходит в одну и ту же точку программы, вводится булева переменная done, которая предотвращает печать значения функции после выхода из цикла в случае, когда точность вычислений не достигнута. Создание подобных переменных - «флагов», принимающих значение «истина» в случае успешного окончания вычислений и «ложь» в противном случае, является распространенным приемом программирования.

 

Измените программу так, чтобы она печатала не только значения аргумента и функции, но и количество просуммированных членов ряда, и выполните программу несколько раз для различных значений аргумента и точности. Выявите зависимость между этими величинами.

 

Можно реализовать ту же логику и без специальной булевой переменной, объединив проверку обоих вариантов выхода из цикла в его заголовке:

 

#include < iostream.h> #include < math.h> #include < float.h> int main () { const int MaxIter = 500; /* максимально допустимое количество итераций */ double x. eps = DBL_EPSILON; cout < < " \n Введите аргумент"; cin > > x; double ch = 1, у = ch; // первый член ряда и нач. значение суммы for (int n = 0; fabs(ch) > eps & & n < MaxIter; n++) { ch *= x * x / ((2 * n + 1) * (2 * n + 2)); // очередной член ряда y+= ch; } if (n < MaxIter) { cout < < " \n Значение функции: " < < у < < " для х = " < < х < < endl; cout < < " вычислено после " < < n < < " итераций" < < endl; } else cout < < " \nРяд расходится! "; return 0; }

 

В этом варианте программы сумма ряда для разнообразия вычисляется с максимально возможной точностью.

 

В библиотеке есть функция cosh(x). вычисляющая гиперболический косинус прототип находится в файле < math. h>. Измените программу так, чтобы она рядом со значением, вычисленным через разложение в ряд, печатала и значение, определенное с помощью стандартной функции. Сравните результаты вычислений.

 

Итак, мы рассмотрели две задачи с использованием циклов. Циклы встречаются в программах повсеместно, и строятся они по одним и тем же принципам. Чтобы избежать ошибок при программировании, рекомендуется:

 

- Проверить, всем ли переменным, встречающимся в правой части операторов присваивания в теле цикла, присвоены до этого начальные значения, а также возможно ли выполнение других операторов;

- Проверить, изменяется ли в цикле хотя бы одна переменная, входящая в условие выхода из цикла;

- Предусмотреть аварийный выход из цикла по достижении некоторого количества итераций;

- Не забывать заключать в фигурные скобки тело цикла, если в нем требуется выполнить более одного оператора.

 

Операторы цикла в языке C++ взаимозаменяемы, но можно привести некоторые рекомендации по выбору наилучшего в каждом конкретном случае.

 

Оператор do while обычно используют, когда цикл требуется обязательно выполнить хотя бы один раз, — например, если в цикле производится ввод данных.

 

Оператором while удобнее пользоваться в тех случаях, когда либо число итераций заранее неизвестно, либо очевидных параметров цикла нет, либо модификацию параметров удобнее записывать не в конце тела цикла.

 

Оператор for предпочтительнее в большинстве остальных случаев. Однозначно — для организации циклов со счетчиками, то есть с целочисленными переменными, которые изменяют свое значение при каждом проходе цикла регулярным образом (например, увеличиваются на 1).

 

Давайте повторим наиболее важные моменты этого семинара.

 

1. Выражение, стоящее в круглых скобках операторов if, while и do while, вычисляется в соответствии с приоритетами операций и преобразуется к типу bool.
2. Если в какой-либо ветви вычислений условного оператора или в цикле требуется выполнить более одного оператора, то они объединяются в блок.
3. Проверка вещественных величин на равенство опасна.
4. Чтобы получить максимальную читаемостью простоту структуры программы, надо правильно выбирать способ реализации ветвлений (с помощью if, switch или условной операции), а также наиболее подходящий оператор цикла.
5. Выражение, стоящее в скобках после ключевого слова switch, и константные выражения в case должны быть целочисленного типа.
6. Рекомендуется всегда описывать в операторе switch ветвь default.
7. После каждой ветви для передачи управления на конец оператора switch используется оператор break.
8. При написании любого цикла надо иметь в виду, что в нем всегда явно или неявно присутствуют четыре элемента: начальные установки, тело цикла, модификация параметра цикла и проверка условия продолжения никла.
9. Если количество повторений цикла заранее не известно, необходимо предусматривать аварийный выход из цикла по достижении некоторого достаточно большого количества итераций.