Введение. Если в электрической цепи действует электродвижущая сила, изменяющаяся по гармоническому закону, то в ней происходят вынужденные электромагнитные колебания
Если в электрической цепи действует электродвижущая сила, изменяющаяся по гармоническому закону, то в ней происходят вынужденные электромагнитные колебания. При этом практический интерес представляют амплитуды силы тока и напряжения на различных участках этой цепи, а также фазовые соотношения в колебаниях силы тока и напряжения.
Рис. 1
Рассмотрим вынужденные электромагнитные колебания в цепи переменного тока, содержащей последовательно соединенные резистор сопротивлением R, конденсатор электроемкостью C и катушку, имеющую индуктивность L (рис. 1). Если частота ν колебаний ЭДС невелика так, что длина электромагнитной волны λ = с / ν (c – скорость света) много больше линейных размеров цепи, то на всех участках этой цепи сила тока I одинакова. Пусть I изменяется по гармоническому закону
Здесь Im – амплитуда силы тока, а ω = 2 π ν – циклическая частота колебаний. Известно, что фаза колебаний напряжения на резисторе совпадает с фазой силы тока:
Параметр UmR = ImR представляет собой амплитуду напряжения на резисторе. Сопротивление катушки переменному току равно XL=ω L. Напряжение на ней опережает фазу тока на π /2 (см. [1-7]). Таким образом, мгновенное значение напряжения на катушке в рассматриваемой цепи описывается уравнением
При этом амплитуда напряжения UmL= Imω L. Сопротивление конденсатора
Амплитуда напряжения на конденсаторе UmC= Суммой UR, UL и UC дается мгновенное значение напряжения U на клеммах генератора. Это напряжение, естественно, будет также изменяться по гармоническому закону с некоторой амплитудой Um, причем фаза его колебаний будет отличаться от фазы силы тока. Обозначим соответствующую разность фаз буквой φ. Таким образом, для любого момента времени выполняется равенство:
Заметим, что в любой момент времени знаки напряжений на катушке и конденсаторе противоположны (разность фаз равна π). Это означает, что в любой момент времени напряжение между точками 4 и 6 (ULC)в схеме, приведенной на рис. 1, определяется разностью модулей напряжений на конденсаторе и катушке. Легко сообразить, что это соотношение выполняется не только для мгновенных значений напряжения, но и для его амплитудных (и действующих) значений:
Следовательно, производя измерения с помощью вольтметра, мы получим, что сумма действующих значений напряжения на отдельных элементах рассматриваемой цепи будет больше действующего напряжения на клеммах генератора. Исключением является лишь особый случай, когда амплитуды напряжений на конденсаторе и катушке одинаковы, т.е. когда Уравнение (5) путем тригонометрических преобразований можно разбить на два уравнения, из которых может быть найдена функциональная связь амплитуды силы тока Im в цепи и амплитуды напряжения Um на клеммах генератора, а также разность фаз φ между силой тока и напряжением на клеммах генератора. Эта задача легко решается при использовании метода векторных диаграмм (см., например, [7]). Рассмотрим конечные результаты решения этой задачи. 1. Амплитуда силы тока в рассматриваемой (последовательной!) цепи дается следующим выражением:
Таким образом, амплитуда силы тока при заданном напряжении на клеммах генератора зависит от частоты вынужденных колебаний ω, сопротивления резистора R, индуктивности катушки L и электроемкости конденсатора C. Если изменять частоту колебаний при неизменных параметрах Um, R, L и C, то можно найти такую частоту, при которой Выражение (7) называют законом Ома для последовательной цепи переменного тока. При этом величина
не остается постоянным во времени. Оно изменяется от -∞ до +∞. Параметр R называется активным сопротивлением. От него зависит количество теплоты, выделяющейся в цепи при протекании переменного тока. Величина Заметим, что в условиях резонанса действующие значения напряжения на конденсаторе и катушке максимальны и равны друг другу. Поэтому рассматриваемое явление называется резонансом напряжений. Найдем амплитуду напряжения на конденсаторе при резонансе (обозначим ее Uр), принимая во внимание, что амплитуда силы тока в этом случае определяется выражением
Параметр Можно также показать, что от добротности колебательного контура зависит ширина резонансной линии: чем выше добротность, тем уже резонансная линия, т.е. меньше интервал частот Δ v, в котором колебательный контур существенно усиливает поданное на него переменное напряжение. Математически эта связь дается формулой
2. Разность фаз между силой тока в цепи и напряжением на клеммах генератора определяется параметрами ω, R, L и C:
В условиях резонанса φ = 0. Если
|


 (1)
(1) (2)
(2) (3)
(3) напряжение на конденсаторе отстает по фазе от изменения силы тока на π /2:
напряжение на конденсаторе отстает по фазе от изменения силы тока на π /2:
 (4)
(4)

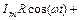

 (5)
(5) (6)
(6) В этом случае напряжение на клеммах генератора будет равно напряжению на резисторе, поскольку UmLC = 0.
В этом случае напряжение на клеммах генератора будет равно напряжению на резисторе, поскольку UmLC = 0. (7)
(7) и амплитуда тока принимает наибольшее значение. Частота
и амплитуда тока принимает наибольшее значение. Частота  называется резонансной частотой. Эта частота соответствует собственной частоте колебаний в LC-контуре. Заметим, что при неизменной частоте переменного тока достигнуть условий резонанса в колебательном контуре можно, изменяя индуктивность L или электроемкость C.
называется резонансной частотой. Эта частота соответствует собственной частоте колебаний в LC-контуре. Заметим, что при неизменной частоте переменного тока достигнуть условий резонанса в колебательном контуре можно, изменяя индуктивность L или электроемкость C. имеет смысл полного сопротивления RLC-цепи переменному току. Следует, однако, учитывать, что выражение (7) связывает не мгновенные значения силы тока и напряжения, а их амплитудные значения. Отношение мгновенных значений
имеет смысл полного сопротивления RLC-цепи переменному току. Следует, однако, учитывать, что выражение (7) связывает не мгновенные значения силы тока и напряжения, а их амплитудные значения. Отношение мгновенных значений (8)
(8) называется реактивным сопротивлением цепи. Реактивное сопротивление не дает вклада в тепловые потери электрической энергии в колебательном контуре. Заметим, что часто активное сопротивление колебательного контура существенно больше омического сопротивления резистора R на постоянном токе. Так, при введении ферромагнитного сердечника в катушку в нем возникают токи Фуко, сопровождающиеся затратами электрической энергии – сердечник нагревается. Это соответствует возрастанию активного сопротивления колебательного контура.
называется реактивным сопротивлением цепи. Реактивное сопротивление не дает вклада в тепловые потери электрической энергии в колебательном контуре. Заметим, что часто активное сопротивление колебательного контура существенно больше омического сопротивления резистора R на постоянном токе. Так, при введении ферромагнитного сердечника в катушку в нем возникают токи Фуко, сопровождающиеся затратами электрической энергии – сердечник нагревается. Это соответствует возрастанию активного сопротивления колебательного контура. и
и  (8)
(8)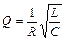 определяет, во сколько раз напряжение на конденсаторе (или катушке) в условиях резонанса больше напряжения на клеммах генератора. Этот параметр называется добротностью колебательного контура. Добротность колебательных контуров, используемых в радиотехнике, достигает сотен единиц. Таким образом, колебательный контур способен значительно усилить переменный электрический сигнал, если частота сигнала соответствует собственной частоте колебательного контура. Это свойство колебательного контура используется в радиотехнике, телевидении для обеспечения избирательности приемника сигналов.
определяет, во сколько раз напряжение на конденсаторе (или катушке) в условиях резонанса больше напряжения на клеммах генератора. Этот параметр называется добротностью колебательного контура. Добротность колебательных контуров, используемых в радиотехнике, достигает сотен единиц. Таким образом, колебательный контур способен значительно усилить переменный электрический сигнал, если частота сигнала соответствует собственной частоте колебательного контура. Это свойство колебательного контура используется в радиотехнике, телевидении для обеспечения избирательности приемника сигналов.
 (9)
(9) (индуктивное сопротивление контура больше его емкостного сопротивления), то φ > 0: изменение напряжения опережает по фазе изменение силы тока. При
(индуктивное сопротивление контура больше его емкостного сопротивления), то φ > 0: изменение напряжения опережает по фазе изменение силы тока. При 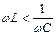 φ < 0: напряжение отстает по фазе от силы тока.
φ < 0: напряжение отстает по фазе от силы тока.


