Основні теоретичні відомості. 1. Визначення мінімального порядку та передаточної функції інверсного фільтру Чебишева
1. Визначення мінімального порядку та передаточної функції інверсного фільтру Чебишева. АЧХ інверсного фільтру Чебишева нижніх частот визначається наступним чином:
де ε – додатне стале число; Cn – поліном Чебишева; ω 1 – початкова частота смуги пропускання (див. рис.1). Частота зрізу знаходиться за формулою:
АЧХ інверсного фільтру Чебишева монотонна у смузі пропускання 0< ω < ω зр та має пульсації у смузі затримки ω > ω 1. Пульсації рівні за значенням та складають
Якщо мінімальне згасання у смузі затримки α 2=-20 lg A 2, то
Рис. 1. АЧХ інверсного фільтра Чебишева 6-го порядку
Отже, для заданого порядку фільтру n, мінімального згасання у смузі затримки α 2 та частоти ω 1 можна знайти значення ε за формулою (4), а за формулою (1) знайти АЧХ, що вимагається. Тоді частоту ω зр та ширину перехідної області TW можна визначити за формулами (2) та (3). Мінімальний порядок n, що забезпечує задані технічні вимоги α 2, ω зр та ω 1 згідно формул (2) і (4) визначається наступним чином:
Рівняння (3) можна представити у вигляді:
Рівняння (5) та (6) можна використати для визначення для знаходження ширини перехідної області TW:
Згідно з формулою (7) для більш вузької перехідної області потрібне більше значення порядку n, що пов'язано зі збільшенням числа пульсацій. Наприклад необхідно знайти мінімальний порядок інверсного фільтру Чебишева, необхідний для реалізації наступних характеристик: α 2=20 дБ, f зр=1000 Гц, TW ≤ 300 Гц. За виразом (6):
За формулою (5:)
Таким чином мінімальний порядок n =4. Знайдемо ширину перехідної області TW за формулою (7):
Отримані результати співпадають з результатами отриманими для фільтру Чебишева. З цього можна зробити висновок, що для заданих припустимих відхилень у смугах затримки та пропускання і ω зр та TW фільтри Чебишева та інверсний фільтр Чебишева мають однаковий порядок. При цьому цей порядок менше необхідного порядку фільтра Баттерворта. Отже, якщо необхідна монотонна характеристика у смузі пропускання, то інверсний фільтр Чебишева за параметрами має перевагу перед фільтром Баттерворта того ж самого порядку. Передаточна функція інверсного фільтра Чебишева у загальному випадку має вид:
Для нормованого фільтра (ω зр=1 с-1) парного порядку (n =2, 4, 6 …) передаточну функцію можна записати у вигляді добутку співмножників
а для непарного порядку (n =3, 5, 7 …):
де Ai та A 0 – сталі числа; ai, bi, сi – нормовані коефіцієнти (див табл. 1). Сталі числа Ai та A 0 пов'язані з коефіцієнтом підсилення фільтру або однієї з його ланок. Для інверсного фільтру Чебишева першого порядку
де K 0 – коефіцієнт підсилення фільтру. Для інверсного фільтру Чебишева другого порядку
де Ki – коефіцієнт підсилення ланки другого порядку. Для реалізації інверсного фільтру Чебишева парного порядку необхідна ланка з передаточною функцією:
де K – коефіцієнт підсилення ланки; a, b та с – нормовані коефіцієнти (див табл. 1); ω зр=2·π f зр. Наприклад необхідно розрахувати передаточну функцію інверсного фільтру Чебишева за наступними даними: порядок фільтру n =4, коефіцієнт підсилення фільтру K =4, частота зрізу f зр=1000 Гц, мінімальне згасання у смузі затримки q =30 дБ. Фільтр буде складатися з двох ланок з передаточною функцією, що визначається рівнянням (11). Оберемо коефіцієнт підсилення кожної ланки K 1= K 2=2, щоб забезпечити необхідний коефіцієнт підсилення самого фільтру K=K 1· K 2=4. З табл. 1 знаходимо для першої ланки: a 1=2, 95105, b 1=0, 630988, c 1=1, 061509; для другої ланки: a 2=17, 199978, b 2=2, 16997, c 2=1, 5121. Отже передаточна функція фільтру матиме вигляд:
АЧХ та ФЧХ фільтру представлено на рис.2. 4. Технічна реалізація інверсних фільтрів Чебишева. Одним з способів реалізації фільтру Чебишева другого порядку є ланка зображена на рис. 3. Ця схема реалізує передаточну функцію (11) ФНЧ з наступними параметрами:
де μ =1+ R 7/ R 6.
Рис. 2. АЧХ та ФЧХ інверсного фільтру Чебишева 4-го порядку
Рис. 2. Схема інверсного фільтру Чебишева 2-го порядку
Методика розрахунку інверсного фільтра Чебишева полягає у наступному. 1. Визначаються нормовані коефіцієнти a, b та c. 2. Обирають номінальне значення ємності C 1≈ 10/ f зр (мкФ). У випадку K ≤ 10 приймають C 2= C 1. (Розрахунок для інших випадків див. […]) 3. За нижче приведеними формулами розраховуємо опори R 1 – R 7.
4. Обираємо номінальні значення опорів найближчі до розрахованих та реалізуємо фільтр або його ланки за схемою на рис. 2.
Таблиця 1. Нормовані коефіцієнти інверсних фільтрів Чебишева
Таблиця 2. Вихідні дані для дослідження
|


 , (1)
, (1) . (2)
. (2)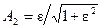 . Ширина перехідної області дорівнює:
. Ширина перехідної області дорівнює: . (3)
. (3)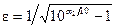 . (4)
. (4)
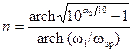 . (5)
. (5) . (6)
. (6) . (7)
. (7) .
. .
. (дБ).
(дБ). . (8)
. (8) , (9)
, (9) , (10)
, (10) ,
,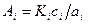 ,
,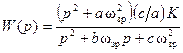 , (11)
, (11) .
. ;
; (12)
(12) ,
,

 ;
;  ;
;  ;
;  ;
;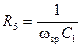 ;
;  ;
; 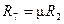 .
.


