Оптимизация потребления в условиях межвременных бюджетных ограничений
Ирвинг Фишер впервые поставил вопрос о возможности оптимизации потребительского выбора путем сопоставления потребления в настоящем и будущем. И. Фишер разработал модель, с помощью которой анализируют то, как рациональные потребители, думающие о будущем, делают межвременной выбор, т.е. выбор, который принимает во внимание принятие решений субъектами в различные периоды времени. Эта модель исследует те ограничения, с которыми сталкивается потребитель, делая выбор между потреблением и сбережением. Предположим, что потребитель живет в двух периодах. В данном случае следует отметить, что если доход первого периода (Yv1) больше потребления этого периода (С1) то экономический субъект кредитует (делает сбережения). Если Yv1-С1: является отрицательной величиной, то он вынужден занимать. В дальнейшем потребитель либо увеличивает свое потребление за счет сбережений и процентов, но ним, либо вынужден оплатить занятый капитал и проценты по займу. · Первый период - потребитель и потребляет (С1), и делает сбережения (S1). Далее будет рассмотрен случай, когда потребитель имеет возможность осуществлять сбережения в первом периоде. · Второй период - экономический субъект только потребляет (С2). Потребление формируется за счет случайного дохода (Yv2) и величины сбережений (S1), возросшей на изменение процентной ставки. Тогда в первом периоде располагаемый доход распадается на две части: Yv1=C1+S1 (5.1) Отсюда: C1=Yv1-S1, S1=Yv1-C1, где Yv1 – реальный располагаемый доход первого периода; C1 - потребление первого периода; S1 - сбережения первого периода. Потребление во втором периоде определяется доходом этого периода плюс накошенными сбережениями с учетом процентов на эти сбережения. Отсюда: C2=Yv2+S1(1+r), (5.2) где С2 - потребление второго периода; Yv2- реальный располагаемый доход второго периода; r - реальная ставка процента. Подставив в (5.2) значение S1 из (5.1), получим С2=Yv2+(1+r)(Yv1-C1)[12]. Раскрыв скобки и произведя элементарные преобразования, получим: C1(1+r)+С2=Y1(1+r)+ Y2 (5.3) Разделив каждый член уравнения (5.3) на 1+r, выведем уравнение межвременного бюджетного ограничения: С2 Y2 С1+ ─ ─ ─ =Y1+ ─ ─ ─ (5.4) 1+r 1+r 1) Левая часть уравнения есть сумма потребления первого и второго периодов, выраженная в благах первого периода. Другими словами, она отражает настоящую дисконтированную ценность потребления, 2) Правая часть равенства представляет собой настоящую дисконтированную ценность дохода. Уравнение показывает все возможные сочетания потребления в 1 и во 2 периодах при данных величинах дохода за весь период жизнедеятельности экономического субъекта. Рассмотрим графическую интерпретацию межвременного бюджетного ограничения (рис. 5.1). Условия построения: 1. Если r = 0, то значение потребления в первом и во втором периодах совпадают с доходами в эти периоды: С1 = Y1; С2 = Y2 (точка D). 2. Если С1=0 => С2=Y1(1+ r)+Y2. Следовательно, точка А имеет координаты [0; Y1(1+r)+Y2] 3. Если С2=0=> С1=Y1+Y2/(1+r). Поэтому координаты точки В ([Y1+Y2]/[1+r]; 0).
Рис. 5. 1. Межвременное бюджетное ограничение Если потребитель изначально имеет какое-либо богатство, предположим, что он получил наследство, то бюджетные ограничения принимают следующий вид: С2 Y2 С1+ ─ ─ ─ =Y1+ ─ ─ ─ + W0 (5.5) 1+r 1+r где W0 – богатство, имеющееся на начало 1-го периода (рис.5.2). В соответствии с новым бюджетным ограничением потребитель имеет возможность больше потреблять в первом и во втором периодах (сдвиг АВ вправо). Если же в «наследство» потребителю достались долги, то величина -W0 будет отрицательной. Чтобы оплатить долги с учетом процентов, он вынужден сокращать потребление (сдвиг АВ влево): BB'=> W0> 0; В" => W0< 0.
Рис. 5.2. Межвременные бюджетные ограничения с учетом наличия первоначального запаса Все потребители стремятся максимизировать функцию полезности двух благ: потребление в первом периоде (C1) и потребление во втором периоде (С2). Предпочтение потребителей между настоящими и будущими, потреблениями описываются семейством кривых безразличия, каждая из которых иллюстрирует равный уровень полезности для потребителя разных наборов потребления сегодня и в будущем. Потребление в первом и втором периодах представлено нормальными благами, т.е. потребители принимают решение о сокращении потребления в первом периоде только при условии, что потребление во втором периоде возрастет. Потребитель, стремясь максимизировать полезность, пытается достичь наиболее высокой кривой безразличия – U1, U2…Un (рис. 5.3). Однако стремления потребителей наталкиваются на бюджетные ограничения.
Рис 5.З. Карта кривых безразличия Следовательно, выбор потребителя зависит от межвременного бюджетного ограничения, которое в свою очередь определяется доходами первого и второго периодов (рис.5. 4).
Рис. 5.4. Семейство кривых безразличия в условиях межвременных бюджетных ограничений Анализируя данный график, можно заключить, что: 1. Угол наклона межвременного бюджетного ограничения относительно 0С1 равен tg α =1+r[13]. 2.Точка касания D линии межвременного бюджетного ограничения и кривой безразличия дает оптимальный объем потребления в первом и во втором периодах. В этой точке угол наклона кривой безразличия и угол наклона линии межвременного бюджетного ограничения совпадают и равны 1+r. 3.Наклон кривой безразличия выражает предельную норму замещения (MRC). Предельная норма замены потребления показывает, какая величина потребления во втором периоде позволит отказаться от 1 единицы потребления в первом периоде 4. Условия оптимизации потребления определяются соотношением: MRC=1+r. Цена выбора характеризует альтернативную стоимость потребления в будущем, выраженную в ценах настоящего.
|






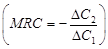 [14].
[14].


