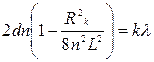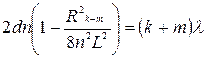Розрахунок різниці ходу інтерферуючих променів
Якщо товщина пластинки значно менша відстані між екраном і пластинкою L, то кут між інтерферуючими променями малий. У цьому випадку при розрахунку різницею ходу непаралельно інтерферуючих променів можна знехтувати. Рис. 3. Розрахунок різниці ходу інтерферуючих променів. 1 і 2 – інтерферуючі промені,
З рис. 3 знаходимо, що різниця ходу цих променів дорівнює
де n – показник заломлення пластинки. Підставляючи сюди
Далі врахуємо, що оскільки відбиття у точці Д відбувається від оптично більш густого середовища, а відбиття у точці С – від оптично менш густого середовища, між променями виникає додаткова різниця фаз, що відповідає додатковій різниці ходу
при Запишемо умови мінімумів k -го і
Відмітимо, що більш високому порядку інтерференції відповідає менший кут падіння променів на пластинку, а відповідно і кільце меншого радіуса на інтерференційній картині. Для кілець, радіус яких значно менше L, з рис.2 випливає
підставляючи (4) у (3), та обмежуючись першим наближенням у розкладанні кореня у ряд по малому параметру
Після простих перетворень із співвідношення (5) знаходимо:
Вимірюючи радіуси двох інтерференційних кілець і відстань між пластинкою і екраном, при відомих значеннях товщини пластинки і довжини хвилі, за формулою (6) можна розрахувати показник заломлення пластинки.
|
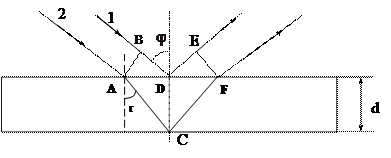
– кут падіння променя, r – кут заломлення.
, отримуємо
. Таким чином, повна різниця ходу променів дорівнює:
мають місце максимуми, а при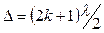 
– мінімуми інтенсивності. Тут k – будь яке число.
-го порядків інтерференції:
, отримуємо
