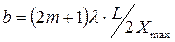Опис метода та установки
У роботі вивчається явище дифракції Фраунгофера на щілині. Дифракцією Фраунгофера називається дифракція плоскої хвилі, яка спостерігається у фокальній площині лінзи або на нескінченності. При цьому у точці спостереження сходиться паралельний пучок променів, які йдуть під однаковим кутом
Рис.1. Схема спостереження дифракції на щілині 1 – лазер, 2 – роздвижна щілина, 3 – фоторезистор, 4 – екран.
Паралельний пучок світла від лазера 1 нормально падає на щілину 2. Дифракційна картина, яка виникає при цьому, спостерігається на екрані 4. Для вимірювання інтенсивності світла у дифракційній картині використовується фоторезистор 3 з маленькою (1 мм шириною) світлочутливою поверхнею, яка розташована перед екраном. Ширина щілини може змінюватися за допомогою мікрометричного гвинта. Фоторезистор можна переміщувати у горизонтальному напрямку поперечно оптичній вісі системи. Положення його відносно оптичної вісі визначається за міліметровою лінійкою. В даній установці екран (і фоторезистор) знаходяться на достатньо великій відстані від щілини, так Тут а – ширина щілини, l – довжина хвилі, L – відстань від щілини до екрану. В цьому випадку ми маємо справу з дифракцією Фраунгофера. Для розрахунку розподілу інтенсивності у дифракційній картині розіб’ємо щілину на елементарні смужки однакової ширини, паралельні краям цілини.
Рис.2. Хід променів у дифракції Фраунгофера на щілині в – ширина щілини, j – кут дифракції,
Відповідно до принципу Гюйгенса-Френеля для знаходження інтенсивності світла у точці спостерігання, кожна елементарна ділянка щілини повинна бути розглянута як вторинне джерело когерентних хвиль. Хвилі від вторинних джерел утворюють у точці спостерігання елементарні коливання з визначеною фазою й амплітудою. Результуюча амплітуда світлового коливання може бути знайдена додаванням коливань від усіх ділянок щілини. Обмежимося цілими кутами дифракції, що дозволить знехтувати зміною амплітуди елементарних коливань при зміні кута дифракції j. При j = 0 усі елементарні коливання додаються в однаковій фазі. Графічне додавання у цьому випадку подано на рис. 3а.
Рис. 3. Векторна діаграма для розрахунку амплітуди результуючого коливання: а) j = 0, б) j – довільний кут, в)
При j ¹ 0 між коливаннями від сусідніх ділянок щілини виникає постійна різниця фаз dФ, яка залежить від j. Результат графічного додавання у цьому випадку показано на рис. 3б. Різниця фаз між коливаннями від крайових елементів щілини, як випливає з рис. 2, дорівнює:
Оскільки різниця фаз dФ між послідовними елементарними коливаннями постійна, а амплітуди у них однакові, на графічній діаграмі ці коливання розташовані вздовж дуги деякого кола з радіусом R з центром у точці О. Довжина дуги дорівнює сумі амплітуд усіх коливань, тобто А 0. З рис. 3б знаходимо:
Наявність максимумів і мінімумів у розподілі інтенсивності світла з’ясовується інтерференцією вторинних хвиль, що розповсюджуються у різних напрямках від різних точок щілини. Якщо j – кут між напрямками падіння променів на щілину і визначеним напрямком, який ми розглядаємо, то умови максимуму освітленості мають вигляд:
а умови мінімуму
де m = ±1; ±2; ±3;..... Розподіл інтенсивності у дифракційній картині на екрані спостерігається залежно від кута дифракції
I0 – інтенсивність світла у напрямку падаючої хвилі У випадку, коли ширина щілини b значно менша відстані L від щілини до екрана (b < < l), дифракція Фраунгофера спостерігається і без лінзи Z. При цьому промені, що ідуть від кінців щілини, практично паралельні.
Розглядаючи рис. 2 для випадку дифракції від щілини, отримуємо вираз для відстані останнього дифракційного максимуму від центрального
Якщо експериментально визначити L, Xmax, m, застосувати формулу (2) та визначене значення
|

 до нормалі. Цей кут називається кутом дифракції.
до нормалі. Цей кут називається кутом дифракції. Схема установки подана на рис. 1
Схема установки подана на рис. 1 що
що  < < 1.
< < 1.
 – різниця ходу між крайовими променями
– різниця ходу між крайовими променями
 Ф – різниця фаз коливань від крайових ділянок щілини, R – радіус дуги ВД,
Ф – різниця фаз коливань від крайових ділянок щілини, R – радіус дуги ВД, г)
г)  .
.

 = (2m + 1)
= (2m + 1) 

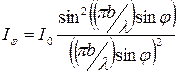
 на якість дифракційної картини помітно впливає ширина щілини. При її збільшенні спостерігається зближення максимумів і мінімумів освітленості до центру.
на якість дифракційної картини помітно впливає ширина щілини. При її збільшенні спостерігається зближення максимумів і мінімумів освітленості до центру.
 , то за допомогою рівняння можна визначити ширину щілини:
, то за допомогою рівняння можна визначити ширину щілини: