Производственная функция
Экономическая деятельность фирмы может быть описана производственной функцией. Производственная функция выражает зависимость между набором факторов производства и максимально возможным объемом продукта, производимым с помощью данного набора факторов. Она может быть описана следующим образом: Q=f (K, L, …).
Хотя производственные функции различны для разных видов производства, все они обладают общими свойствами. 1. Производственная функция всегда конкретна, т. е. предназначается для данной технологии. Новая технология – новая производственная функция. 2. Увеличение объема производства за счет роста только затрат по одному ресурсу имеет предел. Так, нельзя вкладывать средства лишь в капитал, не увеличивая при этом затраты на труд, и наоборот. 3. Факторы производства, как правило, взаимно дополняют друг друга и взаимно заменяют. Например, труд и капитал могут, в некоторой степени, взаимно дополнять и взаимно заменять друг друга. 4. С помощью производственной функции определяется также минимальное количество затрат, необходимых для производства данного объема продукта. Американские экономисты Дуглас и Солоу в 20 – х гг. ХХ века на основе статистических исследований производства зерна за 100 лет рассчитали вклад таких факторов производства, как труд и капитал, в общий прирост выпуска продукции. Оказалось, что увеличение затрат труда на 1% обеспечивает 3/4 прироста выпущенной продукции, а увеличение затрат капитала на 1% дает возможность получить 1/4 прироста продукции. Поскольку эти выводы относились ко всему обществу, то указанные индексы (3/4 и 1/4) назвали агрегатными, а зависимость между выпуском продукции и факторами производства – агрегатной функцией производства Дугласа и Солоу. Дуглас и Солоу показали, что труд является наиболее важным фактором производства, т. к. он обеспечивает наибольшее увелисение выпуска продукции. Производственную функцию можно представить графически с помощью изоквант. Изокванта представляет собой кривую, на которой расположены все сочетания производственных факторов, обеспечивающих одинаковый объем выпуска продукции. Для того чтобы построить изокванту, воспользуемся данными таблицы 8. Таблица 8 Выпуск продукции при различных сочетаниях факторов производства
капитала
Q3=90 Q2=75 Q1=55
Рис. 50. Изокванты Просматривая данные таблицы, можно сделать следующие выводы: 1) по мере роста трудоемкости или затрат капитала объем производства возрастает; 2) один и тот же объем выпуска можно получить при разных сочетаниях труда и капитала. Например, 55 единиц продукции – при сочетании 3 единиц К и 1 единицы L и 3 единиц L и 1 единицы К. Воспользуемся информацией, содержащейся в таблице, чтобы построить изокванты для объемов выпуска 55 единиц, 75 единиц и 90 единиц (рис. 50). Совокупность изоквант, каждая из которых показывает максимальный выпуск продукции, достигаемый при использовании определенных сочетаний факторов производства, представляют собой карту изоквант. Карта изоквант является альтернативным методом описания производственной функции, так же как карта безразличия является одним из способов описания функции полезности. Изокванты показывают гибкость принимаемых фирмами решений по поводу производства продукции. В большинстве случаев они могут добиться определенного объема выпуска товаров и услуг, используя различные сочетания производственных факторов. Особые случаи производственных функций представлены на рисунках 51 и 52.
капитала
Q1 Q2 Q3
Рис. 51. Производственная функция с идеально заменяемыми факторами производства
На рисунке 51 представлена производственная функция с идеально заменяемыми факторами производства. В качестве примера можно привести телефон-автомат на дороге, который обслуживается автоматически или техническим персоналом. Еще один пример – процесс изготовления музыкальных инструментов, который может быть полностью основан на автоматизированном машинном производстве или на высококвалифицированном труде. На рисунке 52 изображена производственная функция с фиксированной структурой использования факторов производства. В этом случае замена одного фактора производства другим невозможна. Затраты
Q2
Затраты труда Рис 52. Производственная функция с фиксированной структурой использования факторов производства
Каждый объем выпуска продукции требует сочетания труда и капитала в определенной пропорции. В итоге изокванты имеют форму прямого угла. Примером такой функции может служить обслуживание такси, когда нужны только один водитель и одна машина. В результате фирма ограничена в выборе способа производства. Угол наклона изокванты показывает, каким образом происходит сохранение постоянного объема продукции при замещении одного фактора производства другим. Его абсолютное значение называется предельной нормой технического замещения (MRTS). MRTS труда капиталом указывает, от какого количества единиц капитала следует отказаться ради одной дополнительной единицы труда. В математической форме МRТС имеет следующий вид:
MRTS имеет тенденцию к понижению. Это объясняется тем что, в конце концов, количество единиц труда увеличивается, а количество единиц капитала уменьшается, вследствие чего дополнительные единицы капитала начинают цениться больше, чем дополнительные единицы труда. В краткосрочном периоде величина капитала не изменяется. Единственным переменным фактором является труд. Поэтому можно говорить о валовом, среднем и предельном продукте переменного фактора – труда. Валовый продукт (TQL) – это количество единиц продукта (Q), произведенное определенным количеством единиц труда (L), или
Средний продукт труда (AQL) –это продукт, произведенный в расчете на единицу труда, или
Предельный продукт труда (MQL) – это изменение в валовом продукте труда (
На основании данных формул можно вывести формулы средних переменных и предельных издержек:
где PL – цена единицы труда.
Анализ с помощью изоквант имеет для производителя очевидные недостатки, т. к. использует только натуральные показатели затрат ресурсов и выпуска продукции. Максимизировать выпуск при данных издержках позволяет прямая равных издержек, или изокоста. Изокоста представляет линию, объединяющую все возможные сочетания ресурсов, которые имеют одинаковую суммарную стоимость. Ее можно представить в алгебраическом
С1 C C2
Рис. 53. Изокоста
виде и в графическом (рис. 53). Если в качестве ресурсов используются труд и капитал, то уравнение изокосты имеет вид: С = РLL + PKK, или К = С/РК – РL/PK*L. Рост бюджета производителя или снижение цен ресурсов сдвигает изокосту вправо (рис. 53, изокоста С2), а сокращение бюджнта или рост цен – влево (рис. 53, изокоста С1).
* Q3 * B Q2 Q1 C L Рис. 54. Pавновесие производителя
Касание изокванты с изокостой опаределяет положение равновесия производителя, поскольку позволяет достичь максимального объема производства при имеющихся ограниченных средствах, которые можно затратить на покупку ресурсов. Учитывая, что в точке В изокванта и изокоста имеют одинаковый наклон и что наклон изокванты измеряется предельной нормой технического замещения, можно записать условие равновесия как MRTSLK = - Предположим, что цены ресурсов остаются неизменными, тогда как бюджет производителя постоянно растет. Соединив точки пересечения изоквант с изокостами, мы получим линию 0S – «путь развития» (рис. 55), показывающую темпы роста соотношения между факторами в процессе расширения производства. Форма кривой «путь развития» зависит, во – первых, от формы изоквант и, во – вторых, от цен на ресурсы (соотношение между которыми определяет наклон изокост). Если линия 0S имеет наклон в сторону линии труда, то труд в ходе развития производства используется в большей мере, чем
L Рис. 55. Кривая «путь развития»
капитал, если в сторону линии капитала – то наоборот. Линия «путь развития» может быть прямой или кривой, исходящей из начала координат. Если расстояния между изоквантами уменьшаются, это свидетельствует о том, что существует возрастающая экономия от масштаба, т. е. увеличение К K K
L L L Рис. 56. Убывающая Рис. 57. Возрастающая Рис. 58. Постоянная экономия от масштаба экономия от масштаба экономия от масштаба
выпуска достигается при относительной экономии ресурсов (рис. 57). Если расстояние между изоквантами увеличивается, это свидетельствует об убывающей экономии от масштаба (рис. 56). В случае, когда увеличение производства требует пропорционального увеличения ресурсов, говорят о постоянной экономии от масштаба (рис. 58). Таким образом, изокванта позволяет не только экономно использовать имеющиеся ресурсы для достижения данного объема производства, но и определить минимально эффективный размер предприятия в отрасли. В случае возрастающей экономии от масштаба фирме необходимо наращивать объем производства, т. к. это приводит к относительной экономии имеющихся ресурсов. Убывающая экономия от масштаба свидетельствует о том, что минимально эффективный размер предприятия уже достигнут. Тем самым анализ выпуска с помощью изоквант позволяет определить техническую эффективность производства. Касание изоквант с изокостой позволяет определить не только технологическую, но и экономическую эффективность, т. е. выбрать технологию, позволяющую обеспечить максимальный выпуск продукции при тех денежных средствах, которыми располагает производитель для организации производства.
|


 Затраты
Затраты
 Трудовые затраты
Трудовые затраты Затраты
Затраты
 Затраты труда
Затраты труда


 капитала
капитала Q3
Q3 Q1
Q1





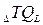 ) вследствие применения дополнительной единицы труда (Δ L), или
) вследствие применения дополнительной единицы труда (Δ L), или

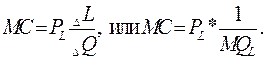
 К
К
 L
L К
К * D
* D

 A
A
 = -
= -  .
. 
 К
К
 S
S













 S S S
S S S








