ОБОСНОВАНИЕ ПРИМЕНЕНИЯ ТЕСТОВЫХ МЕТОДОВ ДЛЯ ДИАГНОСТИРОВАНИЯ ПРОЦЕССА МИКРОШЛИФОВАНИЯ
В соответствии с моделью пластической деформации твердое тело рассматривают как многоуровневую самоорганизующуюся систему, в которой микро-, мезо и макроуровни органически взаимосвязаны, и в которой движение структурных элементов на всех уровнях подчиняются закону подобия. В процессе микрошлифования кристалла в соответствии с принятой моделью пластичного резания воздействие на кристалл происходит на всех уровнях: на микроуровне происходит воздействие зерном режущего инструмента в точку ОП; на мезоуровне происходит раскачивание мезообъема (0, 05мкм), нарушается сдвиговая устойчивость, а срыв поверхности происходит на макроуровне (20-25мкм) При микрошлифовании кристалла задается характеристика обеспечения оптической чистоты на окончательно обработанной поверхности, которая определяется в виде максимально допустимой высоты микронеровностей при отсутствии дефектов в подповерхностном слое. Эта характеристика определяет минимальные линейные размеры деформированного слоя поверхности кристалла на 1 мезомасштабном уровне, который должен образоваться в результате пластической деформации поверхности при формировании фрагментированной субструктуры, состоящей из множества отдельных мезообъемов. Мезообъемы заданного размера формируются в результате внешнего воздействия концентраторов напряжений на микромасштабном уровне. Математически процесс микрошлифования можно представить с одной стороны уравнением 1 порядка, описывающим в УОС статическую составляющую упругой деформации сжатия:
Где J - жесткость системы, Н/мкм; Xвх Xвых - снятый припуск, мкм; Cp - коэффициент пропорциональности, кг х с/мкм. Решение этого уравнения имеет вид:
q - знаменатель затухания подачи по закону геометрической прогрессии; N - количество проходов;
Т - постоянная времени переходных процессов, c. С другой стороны процесс пластического резания носит автоколебательный характер. Анализ осциллограмм, характеризующих динамику состояния каждой конкретной упругой обрабатывающей системы в момент выхода её на размерно-управляемый режим микрошлифования и идентифицирующих динамику состояния параметров каждой такой системы в установившемся режиме динамического равновесия между, с одной стороны, условиями фактического нагружения ритмичным полем (в виде внешних импульсных воздействий микроконцентраторов касательных напряжений) и с другой стороны, фактической реакцией обрабатываемого материала к равномерно периодическому и послойному удалению припуска с его поверхности (в виде отдельных дискретных порций с множеством единичных пластически деформированных " стружек" в каждой такой порции), проявляемой периодически равномерной величиной динамической составляющей упругих деформаций в обрабатывающей системе, показывает, что движение каждой такой (конкретной) упругой обрабатывающей системы в динамике под действием периодической импульсной нагрузки подчинено закону, который наиболее полно может быть описан нелинейным дифференциальным уравнением второго порядка Ван-дер-Поля, напоминающим уравнение для свободных колебаний системы с одной степенью свободы (но с нелинейным членом, описывающим затухание).
Подробное описание составляющих этого уравнения и его решений приведены в пособие „Теория абразивно-алмазной обработки высокотвердых материалов”. Необходимость решения этого уравнения (1.3) обусловлена определением взаимосвязей между всеми безразмерными параметрами упругой обрабатывающей системы. Как правило, для решения задач по механическим колебаниям широко применяют электронные моделирующие устройства. Однако для данной системы под воздействием периодической импульсной нагрузки осуществить это не представляется возможным, в связи с объемностью и сложностью вычислений и невозможностью одновременного учета всех изменяющихся в результате обработки параметров. Существующие попытки увязки статического и динамического процессов, деформаций идущих на разных уровнях имеют грубое приближение, которое не может быть использовано в нашем случае прецизионной размерно-регулируемой бездефектной обработки, кроме того, при отсутствии приборов активного контроля нет возможности непосредственно комплексно измерить все интересующие нас параметры. Для определения таких взаимосвязей необходимо одновременно с процессом обработки осуществлять процесс вычисления соответствующих параметров. Известны тестовые методы идентификации параметров микрошлифования, которые позволяют в реальном масштабе времени идентифицировать и тем самым контролировать фактические параметры процесса. Эти тестовые методы идентификации увязывают статическую и динамическую составляющие упругой деформации в обрабатывающей системе без проведения сложных вычислений и позволяют удерживать поведение УОС в режиме предельного цикла. Поэтому при микрошлифовании кристаллов в отсутствии средств активного контроля очень важна возможность использования тестовых методов для технологической диагностики процесса размерно-регулируемого шлифования по текущим параметрам. На основании их постоянного контроля происходит осуществление адаптивного управления параметрами УОС для получения заданных выходных параметров и для того, чтобы не допустить выхода процесса микрошлифования за пределы области пластичного резания. Тестовыми методами идентифицируют параметры динамического внешнего воздействия на ОП ритмичного поля УОС шлифовального станка, которые определяют условия: - автоколебательного характера процесса пластичного - микрошлифования в мезообъемах с периодическим порционным удалением материала с ОП в виде множества единичных пластически деформированных частичек основного материала в каждой такой порции; - соответствия линейных размеров каждой такой единичной стружки величине микронеровностей Rz на ОП; - сплошности основного монокристалла на ОП после удаления каждой очередной порции из указанного множества единичных пластически деформированных стружек; - формирования диссипативной структуры приповерхностного слоя на ОП; - отсутствие нижележащих нарушенных слоев. Причем, применяя тестовые методы в условиях автоматизированного эксперимента, возможно, не только диагностировать, но и прогнозировать состояние параметров резания путем математического анализа (средствами персонального компьютера в ЧПУ станка) взаимосвязи выходных параметров системы резания как ответной реакции управления её входными параметрами по определенно заданному алгоритму.
1.3. ВЫБОР ДИАГНОСТИРУЕМЫХ ПАРАМЕТРОВ ПРИ РАЗМЕРНОМ МИКРОШЛИФОВАНИИ АЛМАЗОВ. Для автоматизации процесса микрошлифования кристаллов алмазов необходимо постоянно и одновременно с процессом микрошлифования осуществлять технологическую диагностику текущих параметров обработки для стабилизации выходных параметров. При микрошлифовании кристаллов на достаточно малых врезных подачах (порядка 0, 05 мкм) имеет место пластическая деформация в мезообъемах, сопровождающаяся в установившемся режиме резания автоколебаниями упругой обрабатывающей системы (УОС). В этой области для расчетов параметров обработки, возможно, применять классические зависимости, процесса микрошлифования, используемые для микрошлифования металлов. Поэтому при микрошлифовании кристаллов в отсутствии средств активного контроля очень важна возможность использования тестовых методов для технологической диагностики текущих параметров, и на основании их постоянного контроля осуществлять адаптивное управление параметрами УОС для получения заданных выходных параметров и для того, чтобы не допустить выхода процесса микрошлифования за пределы области пластичного резания. Проанализировав основные параметры, характеризующие процесс микрошлифования: -скорость съема припуска; -коэффициент режущей способности круга; -сила или мощность резания; -постоянная времени переходных процессов резания; -вибрации; -упругие деформации, приведенные к зоне резания. В качестве основного параметра для тестовых методов технологической диагностики процесса микрошлифования в УОС удобно рассматривать постоянную времени переходных процессов резания в УОС. К тому же процесс шлифования является наиболее инерционным звеном (на 2-3 десятичных порядка больше, чем в других звеньях) цепи системы адаптивного управления каким-либо параметром системы резания. Поэтому процесс шлифования может быть представлен в общем случае апериодическим звеном первого порядка. Доминирующее влияние на взаимосвязь между силовыми параметрами резания Р и скоростью съема припуска Постоянная времени переходных процессов резания Т характеризует время перехода из одного стационарного состояния в другое стационарное состояние. Постоянная времени переходных процессов резания является параметром, учитывающим факторы воздействия на систему микрошлифования: площади контакта режущего инструмента с обрабатываемой поверхностью, изменения режущей способности шлифовального круга, свойств обрабатывающего и обрабатываемого материалов, жесткости УОС. Но при этом постоянная времени переходных процессов Т непосредственно в ходе обработки может быть только вычислена. Непрерывно диагностируя тестовыми методами постоянную времени переходных процессов Т, в условиях исключения применения средств активного контроля размера и шероховатости обрабатываемого изделия, а также контроля скорости съема припуска, принципиально возможно (при стабильном функционировании процесса в соответствии с принятой математической моделью) автоматическое регулирование постоянной времени переходных процессов Т и силовых параметров резания Р. При этом адаптивное регулирование Р может осуществляться за счет изменения скорости врезания. Возможность использования для каждого конкретного станка тестовых методов определения параметров системы резания в режиме автоматизированного эксперимента и диагностики, при этом Т обусловлена необходимостью априорного определения: 1). Математической модели системы резания, взаимоувязывающей через Т входной – силовой его параметр Р с выходным, т.е. со скоростью съема припуска 2). Границ области, в которой процесс резания стабильно функционирует в соответствии с принятой математической моделью и схемой размерной настройки упругой системы резания, а также в соответствии с алгоритмом получения готового размера; 3). Тестового алгоритма переходного (например, по экспоненте) режима резания, при котором Т оказывает доминирующее влияние на взаимосвязь между входными Р и выходными 4). Вычислительного алгоритма с минимальным числом счетных операций в процессе тестовой отработки, как при статистической обработки информации от измерительных преобразователей, так и при экстраполяции последовательно измеряемых точек экспериментальной кривой в ходе тестовой обработки заготовки на экспоненциальную кривую, с вычислением постоянной времени Т этой экспоненты. Характерной особенностью этих задач является то обстоятельство, что их решения могут быть найдены только в результате проведения экспериментальных исследований. Постоянная времени является функцией двух основных параметров, характеризующих процесс шлифования, т.е. коэффициентов режущей способности шлифовального крута и жесткости системы резания, приведенной к зоне резания. Оба эти параметра зависят от физико-механических факторов процесса шлифования (характеристик абразивного инструмента, материала заготовки, конструкции станка). Как уже ранее отмечалось, постоянная времени представляет собой логарифмический декремент затухания по экспоненциальному закону и определяет время убывания упругой деформации в системе резания с момента выключения врезной подачи круга в заготовку до условно наименьшего (заранее заданного) своего значения при отсутствии износа круга. Наиболее точным способом определения постоянной времени является использование информации о времени tn переходного процесса при выхаживании Т = 0, 33τ. Время переходного процесса может быть представлено суммой временных интервалов между измерениями какого-либо параметра, выполненными на всем участке затухающего переходного процесса до момента его условного окончания. Проведенными экспериментами установлено, что в зависимости от длительности переходных процессов могут быть использованы различные методы для определения постоянной времени. При малой инерционности процесса шлифования удовлетворительные результаты по точности /10-12%/ дает метод прогнозирования постоянной времени по изменению силового параметра резания на переходном этапе в процессе выхаживания. При проведении замеров силового параметра резания на переходном этапе его изменения при выхаживании установлено, что три последовательно замеренные точки лежат на одной прямой. При этом постоянную времени процесса резания ТП целесообразно определять по выражению:
При большей инерционности процесса подсчет постоянной времени по вышеприведенному выражению дает большие погрешности. Поэтому для повышения точности определения постоянной времени процесса на основе данных измерений силового параметра резания здесь может быть применен аппарат регрессивного анализа. Применяя регрессивный анализ для прогнозирования постоянной времени по силовому параметру на участке естественного выхаживания, получим следующее выражение:
где Р0 - значение силового параметра резания в момент выключения принудительной врезной подачи шлифовального круга в заготовку. На основе измерения снимаемого припуска прибором активного контроля также возможно определить постоянную времени процесса. Исследованиями установлена целесообразность прогнозирования этого параметра с учетом экспоненциального характера зависимости скорости съема припуска от времени на переходных участках врезания, в частности при естественном выхаживании после выключения принудительной подачи круга в заготовку. Определение этого параметра при измерении величины съема припуска для малоинерционных систем может производиться по формуле:
При большей инерционности процесса для повышения точности определения постоянной времени процесса резания также целесообразно применение аппарата регрессивного анализа. При этом прогнозирование постоянной времени по съему припуска с заготовки на участке выхаживания, возможно по формуле:
где Как показали экспериментальные исследования, точность, а также скорость вычисления постоянной времени процесса резания на участках выхаживания на основе измерений как силового параметра резания Р так и съема припуска являются равнозначными. Независимость экспериментально исследованных различных методов определения постоянной времени процесса резания и полученная при этом равнозначность результатов, говорят о надежности каждого из этих методов в отдельности и о возможности применения каждого из них для достоверного определения этого параметра резания непосредственно в ходе обработки, т.е. в реальном масштабе времени. При врезном шлифовании алмазов постоянную времени на переходном участке процесса резания, например при выхаживании, можно определить путем последовательных нескольких замеров силового параметра резания, учитывая, при этом, что за каждый ход стола измеряемый силовой параметр сокращается в q раз. Т.е. имеем:
При приближенном определении постоянной времени ТП можно воспользоваться выражением (11), заменяя в нем
С учетом выражения:
а также
С учетом (1.10), режущая способность шлифовального круга при микрошлифовании может быть определена согласно выражению:
Точный учет упругих деформаций в упругой системе резания, приведенных к зоне резания, во многом определяет размерную точность обработки заготовки, особенно если исключено применение активного размерного контроля. При врезном микрошлифовании алмазов к зоне резания величина упругого отжатия Dd системы резания для стационарного участка процесса резания будет определяться выражением:
При технологической диагностике процесса микрошлифования тестовыми методами идентифицируют постоянную времени переходных процессов резания, которая интегрально характеризует поведение УОС как в статике, так и в динамике. Идентифицируя постоянную времени в любой момент фактически можно контролировать выходные параметры обработки: размер и шероховатость.
|

 (1.1)
(1.1) - суммарная врезная подача, мкм;
- суммарная врезная подача, мкм; (1.2) где
(1.2) где  - исходная подача, мкм;
- исходная подача, мкм; - время одного прохода, с;
- время одного прохода, с; - упругая деформация, накапливаемая в УОС, мкм;
- упругая деформация, накапливаемая в УОС, мкм; (1.3)
(1.3) оказывает постоянная времени переходных процессов резания.
оказывает постоянная времени переходных процессов резания. (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7) - значение скорости съема припуска в момент выключения принудительной подачи круга в заготовку.
- значение скорости съема припуска в момент выключения принудительной подачи круга в заготовку. (1.8)
(1.8) , получим:
, получим: (1.9) Анализируя выражения (1.8) и (1.9), следует, что для малоинерционных систем резания при определении в процессе микрошлифования постоянной времени переходных процессов резания достаточно приостановить периодическую подачу круга в заготовку и замерить силовой параметр резания Рi и Рi+1 последовательно соответственно на i – том и (i+1) - м проходах стола.
(1.9) Анализируя выражения (1.8) и (1.9), следует, что для малоинерционных систем резания при определении в процессе микрошлифования постоянной времени переходных процессов резания достаточно приостановить периодическую подачу круга в заготовку и замерить силовой параметр резания Рi и Рi+1 последовательно соответственно на i – том и (i+1) - м проходах стола. (1.10)
(1.10) , где n - порядковый номер хода стола после выключения принудительной подачи, величина съема припуска при выхаживании в процессе микрошлифования будет определяться выражением:
, где n - порядковый номер хода стола после выключения принудительной подачи, величина съема припуска при выхаживании в процессе микрошлифования будет определяться выражением: (1.11)
(1.11) (1.12)
(1.12)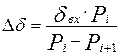 (1.13)
(1.13)


