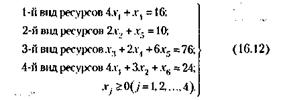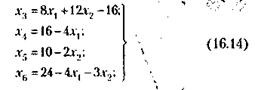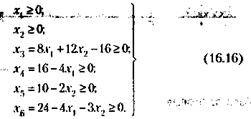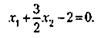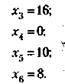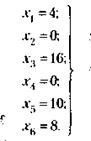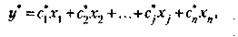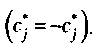Относительные уровни издержек на предприятиях
Распределение ресурсов по предприятиям сопряжено с необходимостью учета ряда ограничений, которые могут быть описаны системой четырех уравнений с шестью неизвестными, аналогичной системе (16.10):
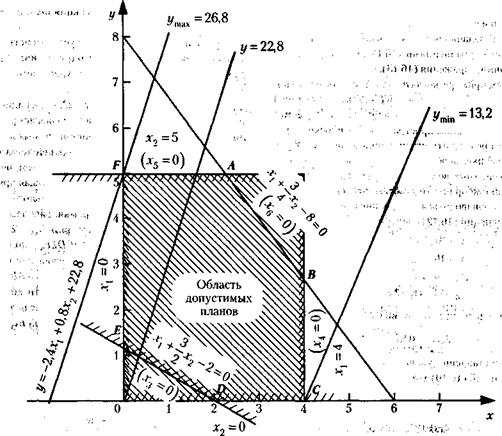
Рис. 16.1. График оптимального распределения ресурсов
Смысл первого уравнения в нашем примере в том, что ресурс вида 1, общий ресурс которого составляет 16 единиц, может размещаться в количестве четырех единиц на предприятии первого типа и одной единицы – на предприятии четвертого типа. Аналогично раскрывается смысл второго и последующих уравнений. Последнее условие говорит о том, что число предприятий не может быть отрицательным. Необходимо определить, какое количество предприятий каждого типа следует иметь, чтобы общие издержки были минимальными. В соответствии с табл. 16.1 целевая функция, подлежащая оптимизации, примет вид:
Решение Решение задачи сводится к выполнению ограничений, заданных уравнениями (16.12), с учетом условия минимизации выражения (16.13). В нашем примере, когда п - т = 2, каждое из ограничительных линейных уравнений (16.12), а также линейная функция (16.13) могут быть представлены геометрически в двухмерном пространстве (на плоскости). Чтобы представить ограничения и целевую функцию на графике, необходимо выразить все известные через независимые величины. Например, x1 и х2, соответствующие координатным осям, относительно которых будет производиться построение (рис. 16.1). Из уравнений (16.12) следует:
Целевая функция примет вид
Из сопоставления уравнения (16.14) и последнего из ограничений (16.10) xj ³ 0 следует:
Каждому из неравенств (16.16) на графике рис. 16.1 соответствует полуплоскость, в пределах которой находятся все допускаемые данным неравенством значения переменной величины xj (j = 1, 2,..., 6). Так, неравенству x1 ³ 0 соответствует полуплоскость вправо от оси х2 (граница ее заштрихована). Неравенству x3 = 8 x1 + 12 х2 - 16 ³ 0 соответствует полуплоскость вправо и вверх от линии граничного значения данного неравенства (при х3 = 0). Уравнение этой линии:
Таким же образом можно построить границы, определяемые другими уравнениями. Неравенствам (16.16) соответствует некоторая область – шестиугольник ABCDEF, образованный границами упомянутых выше полуплоскостей. Эта область может быть названа областью допустимых планов, поскольку любая точка в ее пределах отвечает требованиям наложенных ограничений (16.12). Из всех допустимых планов нас интересует оптимальный план, при котором функция цели у достигает минимума. Целевой функции соответствует семейство параллельных прямых. Рассмотрим одну из них, проходящую через начало координат, что будет иметь место при у = 22, 8. При этом x2 = 3x1. Интересующая нас прямая у = 22, 8, как видно на рис. 16.1, имеет наклон вправо от оси х2. Задаваясь различными значениями у, получим семейство прямых линий, параллельных прямой у = 22, 8, проходящей через точку 0. При этом чем меньше будет значение у, тем, очевидно, правее будет располагаться соответствующая прямая. Поскольку мы добиваемся минимального значения у, то нас будет интересовать прямая, расположенная в наибольшем удалении вправо от прямой у = 22, 8 и проходящая через многоугольник ABCDEF, – прямая ymin. Единственной точкой, соответствующей оптимальному плану, будет та вершина многоугольника ABCDEF, которая одновременно принадлежит области допустимых планов и отвечает требованию минимизации целевой функции у, - вершина С. Из уравнения прямой ЕС, проходящей через точку С, следует, что х1 = 4. Из уравнения прямой DC, проходящей через ту же точку, следует, что x2 = 0. Подставляя полученные значения x1 = 4 и x2 = 0 в уравнения (16.14), определим величины остальных переменных, составляющих оптимальный план:
Таким образом, оптимальный план будет следующим:
Линейная форма (величина издержек) при этом будет минимальной:
На практике встречается ряд задач, аналогичных рассмотренному примеру, но требующих максимизации целевой функции (например, величины дохода или прибыли). При решении этих задач целевая функция рассчитывается по формуле, аналогичной (16.11):
где у* – целевая функция, подлежащая максимизации. Отличие заключается в том, что знаки перед всеми постоянными коэффициентами меняются на обратные
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое эффективность менеджмента? 2. Что такое внутренняя и внешняя эффективность? 3. Что такое критерии эффективности (показатели успешности) менеджмента? 4. Какие требования предъявляются к критериям эффективности менеджмента? 5. Что такое правильное и оптимальное решения? 6. В чем смысл выбора критерия эффективности А. Н. Колмогорова? 7. Как определялись признаки образцовых американских компаний? 8. Что означает признак «лицом к потребителю»? 9. Что означает признак «производительность – от человека»? 10. Что означает признак «пристрастие к действию»? 11. Что означает признак «самостоятельность и предприимчивость»? 12. Что означает признак «побуждение через ценности»? 13. Что означает признак «приверженность неповторимому делу»? 14. Что означает признак «простая форма, скромный штат управления»? 15. Что означает признак «свобода действий и жесткость одновременно»? 16. В чем основные достижения японского менеджмента? 17. Что означает принцип «точно вовремя»? 18. Что такое рентабельность и как она рассчитывается? 19. Приведите примеры расчетов коэффициентов эффективности деятельности фирмы. 20. В чем смысл метода линейного программирования (планирования)? 21. Приведите пример расчета оптимального использования ресурсов.
|