Ротором

Активное сопротивление фазы обмотки статора двигателя с короткозамкнутым ротором рассчитывается так же, как и для двигателя с фазным ротором,

Активное сопротивление фазы короткозамкнутого ротора определяется следующим образом. Как говорилось выше, за фазу обмотки, вы­полненной в виде беличьей клетки, принимают один стержень и два участка замыкающих колец (см. рис. 5.4). Токи в стержнях и замыкающих кольцах различны, поэтому их сопротивления при расчете общего сопротивления фазы должны быть приведены к одному току. Таким образом, сопротивление фазы короткозамкнутого ротора r ₂ является расчетным параметром, полученным из условия равенства электрических потерь в сопротивлении r ₂ от тока I ₂ и суммарных потерь в стержне и участках замыкающих колец соответственно от тока в стержне I _с и тока в замыкающем кольце I _кл реальной машины:

 

(7.35)

 

где I _с — ток в стержне ротора; I _кл — ток в замыкающих кольцах;

r _с - сопротивление стержня; r _кл — сопротивление участка замыкающего кольца, заключенного между двумя соседними стержнями (см. рис. 5.4).

 

Ток I _с называют током ротора и в расчетах обозначают I ₂. Учитывая, что

(7.36)

где из 7.36 получаем

(7.37)

здесь

(7.38)

(7.39)

В этих выражениях I _с - полная длина стержня, равная расстоянию между замыкающими кольцами, м; D _{кл ср} - средний диаметр замыкающих колец, м (см. рис. 5.6),

(7.40)

q _c - сечение стержня, м;

k _r — коэффициент увеличения активного сопротивления стержня от действия эффекта вытеснения тока; при раcчете рабочих режимов в пределах изменения скольжения от холостого хода до номинального для всех роторов принимают k _r = 1;

q _КЛ — площадь поперечного сечения замыкающего кольца, м²;

р _с и р _кл - соответственно удельные сопротивления материала стержня и замыкающих колец, Ом-м, при расчетной температуре (см. табл. 7.5).

 

Таблица 7.5

Удельное электрическое сопротивление материала проводников обмоток

Тип обмотки	Материал	Удельное электрическое сопротивление, Ом∙ м, при температуре, °С
Обмотки из медных проводников или неизолированной шинной меди	Медь
Короткозамкнутые роторы асинхронных машин	Алюминиевые шины   Алюминий литой

 

Примечание. Удельное сопротивление алюминия после заливки в пазы машины несколько повышается в связи с образованием некоторого количества раковин (воздушных включений) и изменением структуры при охлаждении в узких пазах. Поэтому в расчетах принимают участие сопротивление литой алюминиевой обмотки роторов асинхронных машин равным Ом∙ м при температуре 75°С и Ом∙ м при температуре 115°С.

 

Сопротивление r ₂ для дальнейших расчетов должно быть приведено к числу витков первичной обмотки. Выражение коэффициента приведения для сопротивления фазы короткозамкнутого ротора получают, подставляя в (7.20) значения m ₂ = Z ₂ , w ₂=l/2, k _oб2 = 1 и учитывая влияние скоса пазов:

(7.41)

где коэффициент скоса пазов по (3.17)

Обычно значения b_ск выражают в долях зубцового деления ротора t _Z2. При скосе пазов ротора на одно зубцовое деление статора g_СК = p2 p / Z _l. В этом случае в двигателях с 2р = 2 из-за малости угла g_СК принимают k _ск=1.

Приведенное значение активного сопротивления фазы обмотки короткозамкнутого ротора

 

(7.42)

 

Индуктивное сопротивление рассеяния обмотки статора асинхронного двигателя с короткозамкнутым ротором рассчитывается по той же формуле, что и для статора с фазными роторами, т.е.

Входящий в формулу коэффициент магнитной проводимости пазового рассеяния l_п определяется в зависимости от конфигурации пазов по формулам табл. 7.6.

Коэффициент магнитной проводимости лобового рассеяния l_л определяется по (7.47).

Коэффициент магнитной проводимости дифференциального рассеяния l_д1 определяют по формуле

(7.43)

в которой x находится следующим образом.

При открытых пазах статора и отсутствии скоса статора или ротора

(7.44)

 

При полузакрытых или полуоткрытых пазах статора с учетом скоса пазов

(7.45)

В этих формулах t _Z1 и t _Z2 – зубцовые деления статора и ротора;

D_Z определяют по кривой рис. 7.5, а, k _b определяют по (7.24) или (7.27);

b_ск = b _CK/ t _z2 – скос пазов, выраженный в долях зубцового деления ротора.

При отсутствии скоса пазов b _ск = 0; k '_ск определяют по кривым рис. 7.5, д в зависимости от t _Z2/ t _Z1 и b_ск (при отсутствии скоса пазов — по кривой, соответствующей b_ск = 0).

Индуктивное сопротивление обмотки короткозамкнутого ротора определяют по формуле

(7.46)

полученной после подстановки в (7.21) значений m ₂ = Z ₂ и q ₂ = 1/(2р) обмотки короткозамкнутого ротора и введения дополнительного слагаемого l_ск.

 

Коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора рассчитывается по приведенным в табл. 7.5 формулам в зависимости от конфигурации паза ротора (рис. 7.6).

 

Таблица 7.5

Расчетные формулы для определения коэффициентов магнитной проводимости пазового рассеяния короткозамкнутых роторов

 

Рисунок	Расчетные формулы
7.6, а
7.6, б
7.6, в
7.6, г
7.6, д

 

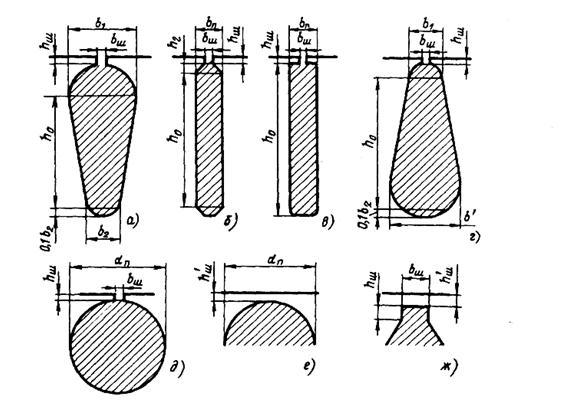
При расчете номинального режима двигателя во всех формулах k _д= 1.

При закрытых пазах ротора любой конфигурации (рис. 7.6, а-д) в расчетных формулах табл. 7.5 нужно при шлицах по рис. 7.6, е слагаемые h _ш/ b _ш заменить на 0, 3+1, 12•10⁶ h _ш/ I ₂; по рис. 7.6, ж - на h _ш/ b _ш + 1, 12· 10⁶ h _ш/ I ₂, где h _ш - толщина ферромагнитной перемычки над пазом, м; I ₂ — ток ротора, А.

 

 

Рис. 7.6. К расчету коэффициентов магнитной проводимости пазового рассеяния короткозамкнутых роторов: а-д — полузакрытые пазы; е, ж — закрытые пазы

 

Коэффициент магнитной проводимости лобового рассеяния рассчитывают в зависимости от размеров и расположения замыкающих колец обмотки по следующим формулам.

В роторах с литыми обмотками при замыкающих кольцах, прилегающих к торцам сердечника ротора (см. рис. 5.6, а), используют формулу

(7.47)

 

Если замыкающие кольца отставлены от торцов ротора (см. рис. 5.6, б), как, например, в обмотке, выполненной из медных или

 

латунных стержней, впаянных в замыкающие кольца, расчет проводят по формуле

(7.48)

В этих формулах D _кл.ср — средний диаметр замыкающих колец по (7.40);

D = 2sinp r / Z ₂ — коэффициент приведения токов в кольце к току в стержне;

h _кл и b _кл — средние высота и ширина колец (см. рис. 5.6);

l ¢ _d — по (7.23).

 

Коэффициент магнитной проводимости дифференциального рассеяния обмотки короткозамкнутого ротора

(7.49)

где

(7.50)

Δ _Z находят по кривым рис. 7.5, а.

Как видно из (7.50), при большом числе пазов ротора, приходящих­ся на пару полюсов, Z ₂/ p ³ 10, без заметной погрешности можно при­нять x=1.

Коэффициент проводимости скоса, учитывающий влияние на ЭДС обмотки ротора скоса пазов,

(7.51)

где b_СК – скос пазов, выраженный в зубцовых делениях ротора. При скосе пазов на одно зубцовое деление ротора b_ск = 1; k_m – коэффициент насыщения магнитной цепи (по 6.27).

Приведенное к числу витков обмотки статора индуктивное сопротивление обмотки короткозамкнутого ротора

x' ₂ = x ₂ γ ₁₂, (7.52)

где γ ₁₂ определяется по (7.41).

Сопротивление схемы замещения r _m (см. рис. 7.1, а) является расчетным. Введением его в схему замещения учитывают влияние потерь в стали статора на процессы в асинхронной машине, поэтому значение сопротивления r _m должно быть принято таким, чтобы выделяющаяся в нем активная мощность была равна мощности, затрачиваемой на потери в стали в реальной машине и отнесенной к одной фазе. Таким образом,

 

r _m= Р _ст/(mI ²_0a), так как активные потери в стали определяются активной составляющей тока холостого хода I _0a.

Сопротивление взаимной индукции обмоток статора и ротора х _m по схеме замещения может быть определено как х _m = E ₁/ I _m.

В расчетной практике параллельное включение сопротивлений r _m и х _m оказалось удобнее заменить последовательно включенными сопро­тивлениями r ₁₂ и х ₁₂ (см. рис. 7.1, б), значения которых определяют из условия

откуда

и

Так как в асинхронных машинах _m ³ х_m, то х₁₂»x_m, а r ₁₂£ x ₁₂, В связи с этим значение r ₁₂ не играет заметной роли при анализе процессов в машине, и в расчетах им часто пренебрегают.

Сопротивления r ₁₂ и x ₁₂ с достаточной для обычных расчетов точ­ностью определяют по следующим формулам:

(7.53)

. (7.54)

Относительные значения параметров. Для удобства сопоставления параметров отдельных машин и упро­щения расчета характеристик параметры асинхронных машин выражают в относительных единицах, принимая за базисные значения номинальное фазное напряжение и номинальный фазный ток статора.

Значения параметров, выраженные в относительных единицах, будем отмечать звездочкой:

(7.55)

Относительные значения одних и тех же параметров схемы замещения различных асинхронных двигателей нормального исполнения незначи­тельно отличаются друг от друга. Так, относительные значения индуктивных сопротивлений рассеяния обмотки статора и приведенного сопротивления обмотки ротора боль­шей частью находятся в пределах x ₁ = 0, 08¸ 0, 14 и х '₂ = 0, 1¸ 0, 16.

Относительные значения сопротивлений взаимной индукции, как правило, в 30—40 раз больше, чем х _1*. Обычно х _12* = 2 ¸ 4.

Относительные значения активных сопротивлений обмотки статора и приведенного сопротивления обмотки ротора близки друг к другу и обычно составляют несколько сотых долей: r _1*» r ¢ _2*» 0, 02¸ 0, 03; лишь в машинах малой мощности их значения несколько увеличиваются. Сопротивление r _12* обычно составляет 0, 05–0, 2.