Решение. Прежде всего, найдем опорные реакции
Прежде всего, найдем опорные реакции. Балка имеет жесткое защемление на правом конце[4] и в этом закреплении при заданной вертикальной нагрузке возникают две опорные реакции: вертикальная реакция RA и реактивный момент MA. Горизонтальная реакция при действии вертикальной нагрузки равна нулю. Это следует из уравнения равновесия " сумма проекций всех сил на горизонтальную ось равна нулю". Определим RA и MA, используя два других уравнения статики. Желательно составлять такие уравнения, в каждое из которых входит только одна неизвестная. В данном случае такими уравнениями являются " сумма проекций всех сил на вертикальную ось (ось z) равна нулю" и " сумма моментов всех сил относительно точки А равна нулю":
– 30× 2 – 15× 2× 1 – 60 + 10× 1× 2, 5 + 30× 4+5 = – 150 + 150 = 0. Теперь определяем внутренние усилия: поперечную силу Q и изгибающий момент М. В соответствии с методом сечений рассекаем балку на каждом участке (в данной задаче их три) произвольным сечением и рассматриваем все силы, расположенные с одной стороны от сечения: слева или справа. Удобно рассматривать все силы с той стороны от сечения, где сил меньше. Начало отсчета координаты x на каждом участке можно выбирать произвольным образом. Например, на рис. 4.6, а начало отсчета x на каждом участке – свое и находится в начале участка. Запишем выражения для Q и М на каждом участке. Участок 1: Рассмотрим силы, расположенные слева от сечения. По определению поперечной силы и с учетом правила знаков для Q (см. рис. 4.5, а):
Здесь По определению изгибающего момента и с учетом правила знаков для М (см. рис. 4.5, б):
где во втором слагаемом Для построения эпюр найдем значения Q и М на границах участка: в начале участка (х 1 = 0) в конце участка ( Участок 2: Снова рассмотрим все силы, расположенные слева от сечения.
Граничные значения Q и М: в начале участка (
в конце участка (
Участок 3: Теперь рациональнее рассмотреть все силы справа от сечения. Тогда
Из этих выражений следует, что поперечная сила на третьем участке – постоянная величина, а изгибающий момент меняется по линейному закону и на границах участка имеет следующие значения: в начале участка ( в конце участка ( Запишем результаты определения внутренних усилий в таблицу, сосчитав численные значения Q и М на границах участков (табл. 1). Таблица 1
Из таблицы видно, что поперечная сила на первом участке меняет свой знак, т. е. график Q пересекает нулевую линию. Это значит, что изгибающий момент на этом участке имеет экстремум. Найдем максимальное значение М на этом участке. Сначала определим то значение координаты х 1, при котором поперечная сила равна нулю. Обозначим это значение координаты х 0 (см. рис. 4.6).
Чтобы найти максимальное значение изгибающего момента, подставим х 0 в выражение для М на первом участке:
По результатам вычислений в таблице строим эпюры Q и М на каждом участке (см. рис. 4.6, б). Не забываем после построения эпюр проанализировать результаты по тем правилам проверки правильности построения эпюр, которые перечислены ранее.
|

 ;
;  ;
; ;
;  Из первого уравнения найдем RA = 30 кН, из второго – МА =5 кН× м. Полученные положительные знаки опорных реакций подтверждают выбранные нами направления опорных реакций: RA – вверх, а МА – против часовой стрелки. Для проверки рекомендуем использовать любое другое уравнение равновесия, например
Из первого уравнения найдем RA = 30 кН, из второго – МА =5 кН× м. Полученные положительные знаки опорных реакций подтверждают выбранные нами направления опорных реакций: RA – вверх, а МА – против часовой стрелки. Для проверки рекомендуем использовать любое другое уравнение равновесия, например 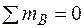 :
: .
. .
. – равнодействующая равномерно распределенной нагрузки, действующей слева от сечения.
– равнодействующая равномерно распределенной нагрузки, действующей слева от сечения. ,
, – плечо равнодействующей равномерно распределенной нагрузки (
– плечо равнодействующей равномерно распределенной нагрузки ( ), взятой слева от сечения (равнодействующая приложена по середине длины отсеченной части балки x 1).
), взятой слева от сечения (равнодействующая приложена по середине длины отсеченной части балки x 1). , а
, а  ;
; )
) 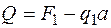 ;
;  .
. .
. ;
; .
. )
) 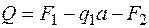 ;
; )
)  ;
; .
. .
. ;
; .
. )
)  ,
, )
)  .
.
 х 0 = 1, 33 м.
х 0 = 1, 33 м. кН× м.
кН× м.


