Решение. Найдем геометрические характеристики заданного поперечного сечения: осевые моменты инерции относительно главных центральных осей
Найдем геометрические характеристики заданного поперечного сечения: осевые моменты инерции относительно главных центральных осей. Сечение имеет только одну ось симметрии, эта ось является одной из главных осей инерции. Обозначим ее z. Вторая главная ось y проходит через центр тяжести сечения. Определим положение центра тяжести сечения по формуле
Статический момент
Здесь первый множитель – удвоенная площадь стенки, второй – координата центра тяжести стенки[5]. Найдя положение центра тяжести сечения, проведем через него вторую главную ось y (см. рис. 4.13). Рекомендуем рисовать сечение в масштабе, тогда по масштабу можно проконтролировать правильность определения центра тяжести сечения. В данном случае очевидно, что центр тяжести должен быть смещен к полке. Теперь определим осевой момент инерции относительно оси y. Находим его как сумму моментов инерции трех фигур: двух стенок (
Здесь
Расстояния h 1 и h 2 показаны на рис. 4.13. Моменты инерции полки и стенки относительно собственных осей y 0 находим по формуле, справедливой для прямоугольника (4.4),
где b – ширина прямоугольника (параллельна оси y 0); h – его высота. Например, для полки
Примечание. Рекомендуем для тренировки аналогично найти момент инерции поперечного сечения относительно оси z, несмотря на то, что в проверке прочности этой балки он не участвует. Строим эпюры поперечной силы и изгибающего момента, выражая ординаты через неизвестный параметр нагрузки (в данной задаче через q – см. рис. 4.12, б). Прежде чем находить положение опасных сечений и опасных точек по эпюрам Q и М, выясним как рационально расположить поперечное сечение балки: полкой вверх или полкой вниз. Поскольку чугун – хрупкий материал и прочность при растяжении у него меньше прочности при сжатии, оптимальным положением сечения является такое положение, при котором максимальные растягивающие напряжения будут меньше максимальных по модулю сжимающих напряжений. В рассматриваемом примере максимальный изгибающий момент отрицателен, то есть балка в сечении, где действует Найдем положение опасных сечений и опасных точек так же, как в двутавровой балке (см. рис. 4.12, в). Поскольку максимальная поперечная сила и наибольший изгибающий момент действуют в данном примере в одном сечении, то опасные точки 1, 1¢, 2 и 3 расположены в одном сечении а–а. Особенностью расчета балок из хрупкого материала является то обстоятельство, что точки 1 и 1¢ не являются равноопасными. Так как хрупкий материал имеет разную прочность при растяжении и сжатии, то проверять прочность надо как в точке 1, в которой действуют максимальные растягивающие напряжения, так и в точке 1¢ с наибольшими сжимающими напряжениями. Если эпюра изгибающих моментов меняет свой знак, как в рассматриваемом примере, то появляется еще одна опасная точка – точка 4 (см. рис. 4.12, в). В этой точке действуют растягивающие напряжения, и поскольку она расположена дальше от нейтральной оси, чем точка 1, величина растягивающего напряжения в точке 4 может оказаться больше, чем в точке 1 несмотря на то, что изгибающий момент в сечении b–b меньше, чем в сечении а–а. Определим допускаемую нагрузку из условия прочности в точке 1, где действуют максимальные растягивающие напряжения:
откуда
Здесь Проверим прочность в остальных опасных точках, используя найденное значение допускаемой нагрузки. В точке 1¢ с наибольшими сжимающими напряжениями
где Для рассматриваемого примера опасной является и точка 4. Условие прочности в этой точке:
Чтобы проверить прочность в точке 2 с максимальными касательными напряжениями, находящейся в напряженном состоянии " чистый сдвиг", необходимо применить теорию прочности, справедливую для хрупкого материала. Например, из теории Мора (4.8) для чистого сдвига получим следующее условие прочности:
где максимальное касательное напряжение Наконец, условие прочности в точке 3, где действуют и нормальные (растягивающие), и касательные напряжения, записываем по теории прочности для " балочного" напряженного состояния, справедливой для хрупкого материала, например по теории Мора (4.8). Нормальные и касательные напряжения в этой точке определяем по формулам (4.1) и (4.2). Если в какой-то точке условие прочности не будет выполняться, необходимо найти новое значение допускаемой нагрузки из условия прочности в этой точке. Примечание; В рассматриваемой задаче, кроме условия прочности, должно выполняться и условие жесткости, т. е. максимальный прогиб не должен превосходить значения допускаемого прогиба. Эта часть задачи является необязательной. Вопрос о нахождении прогибов решается в следующем разделе " Определение перемещений и проверка жесткости балок". 4.1.3. Определение перемещений и проверка жесткости балок (задачи № 19, 20) Рекомендуемая литература Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 8 (§ 8.1–8.5, 8.9). Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 5 (§ 25), гл. 8. Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 7 (§ 7.13–7.14), гл. 11 (§ 11.4, 11.5).
|

 .
. Рис. 4.13. Поперечное сечение
балки
Рис. 4.13. Поперечное сечение
балки
 определяем относительно произвольной оси а – а, перпендикулярной оси z (оси симметрии), как сумму статических моментов фигур, составляющих заданное поперечное сечение. В данном случае сечение разбиваем на три прямоугольника и площадь сечения состоит из площадей трех фигур: двух стенок А с и полки А п:
определяем относительно произвольной оси а – а, перпендикулярной оси z (оси симметрии), как сумму статических моментов фигур, составляющих заданное поперечное сечение. В данном случае сечение разбиваем на три прямоугольника и площадь сечения состоит из площадей трех фигур: двух стенок А с и полки А п:  . Ось а – а рационально расположить так, чтобы статический момент одной из фигур равнялся нулю. Это произойдет, если ось а – а провести через центр тяжести какой-то фигуры, например, через центр тяжести полки (см. рис. 4.13). Тогда статический момент полки равен нулю и полный статический момент Sa равен удвоенному статическому моменту стенки:
. Ось а – а рационально расположить так, чтобы статический момент одной из фигур равнялся нулю. Это произойдет, если ось а – а провести через центр тяжести какой-то фигуры, например, через центр тяжести полки (см. рис. 4.13). Тогда статический момент полки равен нулю и полный статический момент Sa равен удвоенному статическому моменту стенки: .
. ) и полки (
) и полки ( ). Для определения момента инерции каждой фигуры используем формулу
). Для определения момента инерции каждой фигуры используем формулу .
. – момент инерции фигуры относительно оси y 0, проходящей через центр тяжести фигуры и параллельной оси y, а – расстояние между осями y и y 0. Таким образом,
– момент инерции фигуры относительно оси y 0, проходящей через центр тяжести фигуры и параллельной оси y, а – расстояние между осями y и y 0. Таким образом, .
. ,
, .
. , изгибается выпуклостью вверх и растягивающие напряжения будут в верхних волокнах. Поэтому располагаем поперечное сечение так, чтобы центр тяжести сечения был ближе к верхним волокнам, т. е. полкой вверх.
, изгибается выпуклостью вверх и растягивающие напряжения будут в верхних волокнах. Поэтому располагаем поперечное сечение так, чтобы центр тяжести сечения был ближе к верхним волокнам, т. е. полкой вверх. ,
, .
. – момент сопротивления растяжению;
– момент сопротивления растяжению;  – расстояние до наиболее растянутого волокна показано на рис. 4.13. Для рассматриваемого примера
– расстояние до наиболее растянутого волокна показано на рис. 4.13. Для рассматриваемого примера  и
и  .
.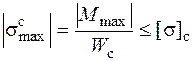 ,
, – момент сопротивления сжатию. (Расстояние
– момент сопротивления сжатию. (Расстояние  показано на рис. 4.13.)
показано на рис. 4.13.) .
. ,
, определяем по формуле Журавского (4.2), в которой статический момент
определяем по формуле Журавского (4.2), в которой статический момент  находим для отсеченной части, расположенной по одну (любую) сторону от нейтральной оси.
находим для отсеченной части, расположенной по одну (любую) сторону от нейтральной оси.


