Решение. Строим эпюры Q и М. По построенным эпюрам Q и М (рис
Строим эпюры Q и М. По построенным эпюрам Q и М (рис. 4.10, б) найдем положение опасных точек в двутавровой балке. Сначала покажем на фасаде балки опасные сечения. Кроме опасных сечений, где действуют максимальный изгибающий момент (сечение а–а на рис. 4.10, в) и наибольшая поперечная сила (сечение b–b на рис. 4.10, в), в двутавровой балке существует еще одно опасное сечение – это сечение, где Q и М одновременно имеют большие значения. В рассматриваемом примере это сечение с–с на рис. 4.10, в. В опасных сечениях находятся опасные точки. В сечении а–а – точки 1, 1¢ с максимальными нормальными напряжениями, в сечении b–b – точка 2, в которой действует наибольшее касательное напряжение. Особенностью проверки прочности двутавровой балки является появление новых по сравнению с балками круглого и прямоугольного сечений опасных точек. Это связано с особенностью эпюры распределения касательных напряжений по высоте двутавра. Точки 3, 3¢, находящиеся в сечении с–с и расположенные в крайних точках стенки на сопряжении с полкой (рис. 4.10, в), опасны, так как в них одновременно действуют большие нормальные и большие касательные напряжения. Подберем размер двутавра (номер двутавра) из условия прочности в точках 1, 1¢ – именно эти точки являются, как правило, наиболее опасными, а затем проверим прочность в остальных опасных точках. Точки 1, 1¢ находятся в линейном напряженном состоянии (рис. 4.9, а) и условие прочности в этих точках имеет вид
Отсюда определяем необходимый момент сопротивления
и в соответствии с ГОСТ 9239–89 подбираем двутавр № 33, у которого
После того, как найден номер двутавра, необходимо убедиться, что выполняются условия прочности в остальных опасных точках. Точка 2, в которой нормальные напряжения равны нулю, а касательные – максимальны, находится в напряженном состоянии " чистый сдвиг" и условие прочности в ней записывается по теории прочности, справедливой для пластичных материалов (4.9) или (4.10). Максимальные касательные напряжения находим по формуле Журавского (4.2). Рассмотрим подробно как находить статический момент отсеченной части
где А – площадь фигуры;
В этой формуле первое слагаемое – статический момент полки, а второе – статический момент половины стенки. Заметим, что для стандартных двутавров статический момент половины сечения задан в сортаменте (обозначен
Сравнивая максимальное касательное напряжение согласно третьей теории прочности с Проверим прочность в точках 3, 3¢, которые находятся в " балочном" напряженном состоянии (см. рис. 4.4). Найдем напряжения, действующие в точке 3. Нормальное напряжение ищем по формуле (4.1). Координата точки 3
Положительный знак полученного напряжения показывает, что в точке 3, расположенной выше нейтральной оси, действует растягивающее напряжение. Для определения касательного напряжения по формуле Журавского получим сначала статический момент отсеченной части. Отсеченной частью сечения для точки 3 будет полка (см. рис. 4.11, б) и
Так как точка 3 находится в стенке двутавра, то
Подставляя найденные значения s и t в условие прочности по третьей теории (4.9), убеждаемся в том, что оно удовлетворяется:
На этом процесс подбора двутавра заканчивается.
Примечание. В условии задачи № 17 есть пункты 7 и 8 [4].в которых требуется исследовать напряженное состояние произвольной точки двутавра. (Выполнение этой части задачи необязательны для студентов заочной формы обучения, студенты дневной и вечерней форм обучения могут выполнять эти пункты по требованию преподавателя) Эта часть задачи не имеет отношения к проверке прочности двутавра, носит академический характер и необходима для лучшего освоения теории изгиба. После того, как Вы выбрали произвольную точку, расположенную в сечении, где и Q, и М не равны нулю, найдите нормальное и касательное напряжения в этой точке по формулам (4.1), (4.2), используя те навыки, которые Вы приобрели при определении напряжений в опасных точках. Выделите вокруг исследуемой точки элементарный параллелепипед (элемент) и покажите на рисунке действующие на гранях элемента напряжения с учетом их знаков. Дальше определите главные напряжения и положение главных площадок, применяя знания, полученные при изучении разд. 2 " Исследование плоского напряженного состояния" в [5]. Поверните на рисунке элемент по главным направлениям и покажите на его гранях главные напряжения.
|

 .
.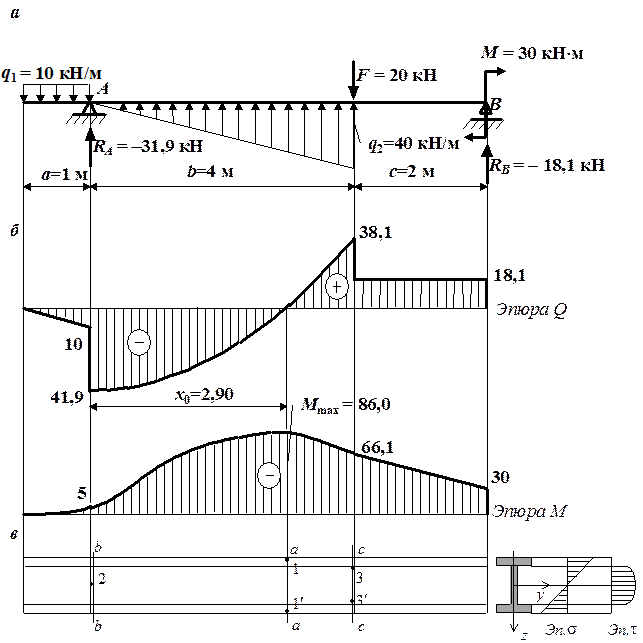 Рис. 4.10. К решению примера 2 о проверке прочности двутавровой балки:
а – схема балки с нагрузками; б – эпюры внутренних усилий;
в – опасные сечения и опасные точки
Рис. 4.10. К решению примера 2 о проверке прочности двутавровой балки:
а – схема балки с нагрузками; б – эпюры внутренних усилий;
в – опасные сечения и опасные точки
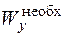 . По таблице сортамента прокатной стали (например, в [1]) подбираем номер двутавра, у которого момент сопротивления
. По таблице сортамента прокатной стали (например, в [1]) подбираем номер двутавра, у которого момент сопротивления 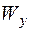 имеет близкое к
имеет близкое к  ). Для балки, изображенной на рис. 4.10, выполненной из стали с допускаемым напряжением 160 МПа,
). Для балки, изображенной на рис. 4.10, выполненной из стали с допускаемым напряжением 160 МПа, см3,
см3, см3.
см3. Рис. 4.11. Отсеченные части сечения:
а – для точки 2;
б – для точки 3
Рис. 4.11. Отсеченные части сечения:
а – для точки 2;
б – для точки 3
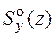 , входящий в формулу Журавского. Статический момент отсеченной части зависит от того, где находится точка, в которой определяется касательное напряжение. Чтобы найти отсеченную часть, надо мысленно разрезать поперечное сечение через точку, в которой ищем t, перпендикулярно направлению касательного напряжения. Любая из " отрезанных" частей может считаться отсеченной. Для точки 2 отсеченная часть сечения показана на рис. 4.11, а (заштрихованная часть) – это половина сечения. Для простых фигур (прямоугольник, круг), положение центра тяжести которых известно, статический момент находится по формуле
, входящий в формулу Журавского. Статический момент отсеченной части зависит от того, где находится точка, в которой определяется касательное напряжение. Чтобы найти отсеченную часть, надо мысленно разрезать поперечное сечение через точку, в которой ищем t, перпендикулярно направлению касательного напряжения. Любая из " отрезанных" частей может считаться отсеченной. Для точки 2 отсеченная часть сечения показана на рис. 4.11, а (заштрихованная часть) – это половина сечения. Для простых фигур (прямоугольник, круг), положение центра тяжести которых известно, статический момент находится по формуле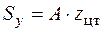 ,
, – координата центра тяжести (при вычислении статического момента отсеченной части знак координаты не учитывается, в этом случае
– координата центра тяжести (при вычислении статического момента отсеченной части знак координаты не учитывается, в этом случае 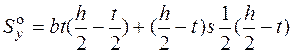 .
. ) и для найденного двутавра № 33
) и для найденного двутавра № 33  см3. В формуле Журавского (4.2) для точки 2
см3. В формуле Журавского (4.2) для точки 2  – толщина стенки двутавра,
– толщина стенки двутавра, 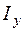 – осевой момент инерции находим по таблице сортамента прокатных двутавров (обозначен
– осевой момент инерции находим по таблице сортамента прокатных двутавров (обозначен 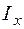 ). Подставляя данные для двутавра № 33, получим
). Подставляя данные для двутавра № 33, получим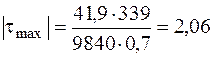 кН/см2.
кН/см2. кН/см2, убеждаемся, что условие прочности в точке 2 выполняется.
кН/см2, убеждаемся, что условие прочности в точке 2 выполняется.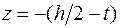 и
и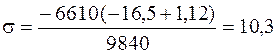 кН/см2.
кН/см2.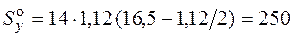 см3.
см3. 0, 7 см. Тогда касательное напряжение в точке 3
0, 7 см. Тогда касательное напряжение в точке 3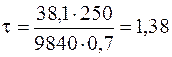 кН/см2.
кН/см2.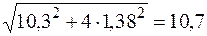 < 16 кН/см2.
< 16 кН/см2.


