Основные определения. Под действием нагрузки происходит деформация балки: ось балки искривляется, точки оси балки перемещаются по вертикали[6]
Под действием нагрузки происходит деформация балки: ось балки искривляется, точки оси балки перемещаются по вертикали[6], сечения балки, оставаясь после деформации перпендикулярными изогнутой оси, поворачиваются. Вертикальное перемещение произвольной точки оси балки, то есть перемещение вдоль оси z, будем называть прогибом и обозначать w (х). Угол поворота произвольного сечения обозначим j(х). Очевидно, что угол поворота произвольного сечения равен углу поворота оси балки в сечении
При проектировании конструкций часто ограничивают не только напряжения (требуется удовлетворить условию прочности), но и деформации (требуется обеспечить выполнение условия жесткости). Для балок условием жесткости является условие, ограничивающее максимальный прогиб, т. е.
где Рассмотрим два наиболее часто используемых способа определения перемещений балок (прогибов и углов поворота): способ, основанный на интегрировании приближенного дифференциального уравнения изогнутой оси балки, называемый аналитическим способом, и метод Максвелла – Мора.
|

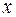 . Прогибы и углы поворота трех балок показаны на рис. 4.14. Известно, что функции w (х) и j(х) связаны между собой такой зависимостью:
. Прогибы и углы поворота трех балок показаны на рис. 4.14. Известно, что функции w (х) и j(х) связаны между собой такой зависимостью: . (4.14)
. (4.14) , (4.15)
, (4.15) Рис. 4.14. Деформации балок при изгибе
Рис. 4.14. Деформации балок при изгибе
 – допускаемый прогиб, который задается в долях от длины пролета балки l и в зависимости от типа проектируемой конструкции может находиться в пределах от
– допускаемый прогиб, который задается в долях от длины пролета балки l и в зависимости от типа проектируемой конструкции может находиться в пределах от  до
до 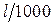 .
.


