Решение. Рамка будет находиться в равновесии, когда результирующий момент сил, действующий на рамку, равен нулю
М1 = рm B sin a, где р m = NIS = NIa2 - магнитный момент рамки; В - индукция магнитного поля; a - угол между вектором М2=Сj. Из условия равновесия Ia2NB sin a - Сj = 0, откуда
B = Сj/(Ia2NB sin a). Подставим числовые значения: В = 10 -3× 60 / 1× 4× 100× 0, 5 = 30 мТл.
2. Прямой бесконечный проводник имеет круговую петлю радиусом R =80 см. Определить силу тока в проводнике, если известно, что в точке А магнитная индукция B = 12, 5 мкТл.
Векторы В1 и В2 на рисунке в точке А будут направлены в одну сторону перпендикулярно плоскости рисунка от нас, тогда можно записать
откуда
Подставим числовые значения:
3. Квадратная рамка расположена в одной плоскости с длинным прямым проводником с током I0 =5 А. Сторона рамки 8 см. Проходящая через середины противоположных сторон ось рамки параллельна проводу и отстоит от него на расстоянии, которое в n = 1, 5 раза больше стороны рамки. Найти поток вектора
Прямой проводник с током создает вокруг себя неоднородное магнитное поле с индукцией
которая уменьшается с увеличением расстояния от проводника. Направление вектора индукции будет совпадать с направлением нормали к рамке. Так как магнитное поле неоднородное, поверхность, ограниченную рамкой, разобьём на элементарные площадки dS = a× dr, в пределах которых магнитную индукцию можно считать постоянной величиной (см. рисунок). Тогда поток магнитной индукции (магнитный поток) через элементарную площадку
dФ m = B·dS·cos 0° = B× а× dr = m 0I0 ·a·dr/(2pr).
Полный поток вектора
Подставим числовые значения: Фm = 4p× 10–7× 5× 0, 08× (ln 2)/2p = 5, 545× 10–8 Вб.
|


 Рамка будет находиться в равновесии, когда результирующий момент сил, действующий на рамку, равен нулю, т.е.
Рамка будет находиться в равновесии, когда результирующий момент сил, действующий на рамку, равен нулю, т.е.  , где М1 - момент сил, действующих на рамку с током со стороны магнитного поля; М2 - момент упругих сил.
, где М1 - момент сил, действующих на рамку с током со стороны магнитного поля; М2 - момент упругих сил.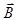 и нормалью к плоскости рамки. Как видно из рисунка, угол a =90°– j =30°.
и нормалью к плоскости рамки. Как видно из рисунка, угол a =90°– j =30°. Решение
Решение По принципу суперпозиции индукция магнитного поля в точке А равна векторной сумме индукций магнитных полей, созданных бесконечно длинным проводником с током I (В1) и круговым током в его центре (В2):
По принципу суперпозиции индукция магнитного поля в точке А равна векторной сумме индукций магнитных полей, созданных бесконечно длинным проводником с током I (В1) и круговым током в его центре (В2): .
.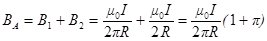 ,
, .
. А.
А.
 Решение
Решение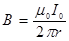 ,
, .
. 4. Между полюсами электромагнита требуется создать магнитное поле с индукцией В =1, 4 Тл. Длина железного сердечника l 1=40 см, длина межполюсного пространства l 2=1 см, диаметр сердечника D =5 см. Какую ЭДС нужно взять для питания обмотки электромагнита, чтобы получить требуемое магнитное поле, используя медную проволоку площадью поперечного сечения S =1 мм 2? Какая будет при этом наименьшая толщина b намотки, если считать, что предельно допустимая плотность тока j =3 МА/м 2?
4. Между полюсами электромагнита требуется создать магнитное поле с индукцией В =1, 4 Тл. Длина железного сердечника l 1=40 см, длина межполюсного пространства l 2=1 см, диаметр сердечника D =5 см. Какую ЭДС нужно взять для питания обмотки электромагнита, чтобы получить требуемое магнитное поле, используя медную проволоку площадью поперечного сечения S =1 мм 2? Какая будет при этом наименьшая толщина b намотки, если считать, что предельно допустимая плотность тока j =3 МА/м 2?


