Расчет деревянных элементов на устойчивость плоской формы деформирования
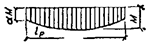
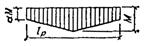
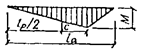
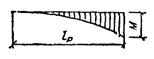
4.17. Принятые в СНиП II-25-80 формулы для расчета на устойчивость плоской формы деформирования прямолинейных и криволинейных изгибаемых и сжато-изгибаемых деревянных элементов прямоугольного сечения получены из решения соответствующих дифференциальных уравнений равновесия упругодеформируемых стержней. Концевые граничные условия заданы во всех случаях одинаковые, при которых опорные сечения не могут вращаться относительно продольной оси стержня, но свободно поворачиваются в плоскости наибольшей и наименьшей жесткости относительно главных осей инерции. Поперечное сечение вдоль оси постоянное или переменное по высоте. Нагрузка действует в плоскости наибольшей жесткости. Рассмотрены случаи, когда кроме концевых закреплений стержень имеет непрерывное или дискретное подкрепление из плоскости деформирования вдоль сжатой или растянутой кромки. 4.18. Специфика древесины как анизотропного материала учитывается при назначении основных расчетных констант (безразмерных параметров) Экваториальный и полярный моменты инерции прямоугольного сечения соответственно равны: Jy = b 3 h /12 и Jd ≈ b 3 h /3. Отсюда следует, что отношение изгибной к крутильной жесткости составит γ = EJy /(GJd) = 20/4 = 5. 4.19. Влияние схемы нагружения и различных по форме эпюр изгибающих моментов, условий подкрепления кромок, переменной жесткости учитывается введением соответствующих коэффициентов к принятым за эталон критическим значениям: осевой силы для сжатого стержня N э = π 3 EJy / l 2 = φ э R вр.с F бр; (23) момента для стержня, подверженного чистому изгибу: M э= π Из (23) следует, что φ э = π 2 EJy /(l 2 R вр.с F) ≈ 3000/λ 2у, аиз (24) φ M = π тогда при иных условиях имеем N кр= KNN эи M кр= KMM э, где KN и KM - коэффициенты, получаемые в результате решения соответствующих краевых задач, которые приводят решаемый случай к принятым за эталон по формулам (23) и (24). Отсюда вытекают зависимости φ р N = KN φ э и φ р M = KM φ M, где φ р M и φ р N - расчетные значения коэффициентов для рассматриваемых случаев. 4.20. Коэффициенты KN и KM зависят от различных факторов. Поэтому представляется целесообразным провести их дальнейшую дифференциацию по определяющим факторам: KN = K п NK ж N; KM = K ф K п MK ж M, где K п N - коэффициент влияния подкрепления кромки при центральном сжатии стержня постоянного поперечного сечения; K п M - коэффициент влияния подкрепления растянутой кромки при чистом изгибе элемента постоянного сечения; K ж N и K ж M - см. п. 4.4. По своему смыслу эти коэффициенты являются коэффициентами приведения элемента с подкрепленной кромкой к эталонному. Они показывают, во сколько раз критическое усилие или критический момент элемента постоянного сечения с подкрепленной кромкой больше критического усилия или критического момента того же элемента без подкрепления. Для элементов без подкрепления K п N = 1 и K п M = 1. 4.21. Формулы (24) и (34) СНиП II-25-80 для определения коэффициентов K п N и K п M распространяются на элементы прямолинейного и кругового очертания. Они получены из решения задачи устойчивости дугообразной полосы, нагруженной постоянной силой N и моментом M (по теории В.З. Власова), которое приводит к зависимости M + Nh /3 = EJy [(h 2/4)(π n / l)2 + h / r 0 + l 2/(r 20π 2 n 2)] + GJd (h / r 0 + 1), (25) где l - расстояние по дуге между закрепленными сечениями; n - число полуволн синусоиды собственной формы выпучивания из плоскости; r 0- радиус кривизны дуги по осевой линии. Зависимость (25) в самом общем виде может быть заменена выражением M + AN = D, (26) если M = 0, AN кр= D и N кр = D / A, при N = 0 M кр = D. Из (26) имеем M / D + AN / D = 1, откуда N / N кр+ M / M кр = 1. (27) Здесь N кр и M кр - критические значения силы N и момента M при их раздельном действии. Используя условие EJy (GJd) = 5 и полагая n = 1 из (25), получим N кр = (3 GJd / h 2)[1 + 12, 5(h / l)2 + 10α р(h / l)], (28) M кр = (GJd / h)[1 + 12, 5(h / l)2 + 10α р(h / l)], (29) где α р = l / r 0. Принимая во внимание, что в данном случае KN = K п N = N кр/ N эи KM = K п M = M кр/ M э, после подстановки из формул (23), (24), (28), (29) выражений N э, M э, N кр, M кр получим формулы (24) и (34) СНиП II-25-80. Найденные зависимости соответствуют решению задачи устойчивости плоской формы деформирования дугообразной полосы, для которой эффект закрепления кромки учтен, как для прямой полосы. Это допущение оправдано тем, что оно компенсирует влияние других факторов, не учитываемых исходными уравнениями. К таким факторам, в частности, надо отнести деформации поперечных сечений. 4.22. Если по растянутой или менее напряженной кромке сжато-изгибаемого элемента имеются точечные (дискретные) подкрепления, то необходимо вводить дополнительный поправочный множитель в зависимости (28) и (29). Полоса с дискретными подкреплениями по кромке представляет собой многократно статически неопределимую систему и ее расчет требует разработки специальных методов. Поэтому в СНиП II-25-80 приняты для этого случая приближенные формулы, основанные на соображениях, изложенных ниже. Коэффициенты подкрепления При дискретных подкреплениях вдоль кромки значения коэффициентов K п N и K п M будут возрастать от единицы (при «нулевом» числе подкреплений) до значении (30) и (31). Указанные предельные случаи позволяют составить непротиворечивые формулы для этих коэффициентов: где Если теперь в (32) подставить выражения из (30), (31), (33), то получим следующие формулы для коэффициентов подкрепления: Данные формулы соответствуют формулам СНиП II-25-80 (34) и (24) при α р = 0. Надо иметь в виду, что m равняется числу промежуточных подкрепленных точек кромки стержня, не считая закреплений его концевых сечений. 4.23. Влияние формы эпюры моментов на величину критического значения ее максимума для изгибаемого элемента постоянного сечения учитывается коэффициентом K ф (см. п. 4.20), который является коэффициентом приведения стержня с произвольной эпюрой моментов к тому же стержню при чистом изгибе. Значения этого коэффициента всегда больше единицы и определяются по формулам табл. 2 прил. 4 СНиП II-25-80. В табл. 18 даны формулы для определения коэффициента K ф, охватывающие более широкий набор форм эпюр моментов. При дискретном подкреплении сжатой кромки изгибаемого или сжато-изгибаемого элемента в промежуточных точках пролета коэффициент K ф следует принимать по наиболее невыгодному в отношении устойчивости участку эпюры моментов, ограниченному с обеих сторон точками закрепления. 4.24. Влияние переменности высоты поперечного сечения по длине элемента на величину критических усилий при центральном сжатии и поперечном изгибе учитывается коэффициентами K ж N и K ж M. Эти коэффициенты приводят элемент переменного сечения к элементу постоянного сечения при прочих равных условиях. Для элементов постоянного сечения K ж N = 1 и K ж M = 1. Для случая, когда ширина поперечного сечения постоянна, а высота изменяется по линейному закону, значения этих коэффициентов приведены в табл. 1 и 2 прил. 4 СНиП II-25-80. Таблица 18
4.25. Влияние масштабного фактора на величину коэффициента вформуле (23) СНиП II-25-80 рекомендуется учитывать введением в знаменатель правой части этой формулы дополнительного коэффициента m б из табл. 7 указанных норм. 4.26. Центральной формулой для проверки устойчивости плоской формы деформирования является N / где N, M д - расчетные значения нормальной силы и изгибающего момента; N кр = φ э R с F и Формула (35) строго справедлива при n = 1 для элементов постоянного сечения с подкрепленной кромкой, находящихся в условиях сжатия и чистого изгиба (N = const; M = const) и при n = 2 для элементов постоянного сечения без промежуточных подкреплений, находящихся при тех же условиях. Так как задачи плоской формы деформирования решены в упругой постановке, то коэффициенты φ э и φ м могут принимать значения больше единицы. Если φ э> 1 и φ м> 1, то проверка устойчивости плоской формы деформирования не требуется. Когда же только один из коэффициентов больше единицы, такая проверка необходима с подстановкой в формулу (33) СНиП II-25-80 вычисленных значений φ э и φ м. Значения коэффициента φ э для любой гибкости определяются по формуле φ э = 3000/λ 2. Внецентренно сжатые и сжато-изгибаемые элементы должны проверяться на устойчивость из плоскости изгиба на действие только сжимающей силы N (СНиП II-25-80, пп. 4.2, 4.3), если гибкость из плоскости изгиба λ y < 70 и напряжение от сжатия выше напряжения от изгиба σ с> σ и.
|

 / R вр.с = 300; E / R вр.н = 200 и E / G = 20.
/ R вр.с = 300; E / R вр.н = 200 и E / G = 20. = φ м R вр.н W. (24)
= φ м R вр.н W. (24) /(lR вр.н W) = 6π b 3 hE /(6
/(lR вр.н W) = 6π b 3 hE /(6  bh 2 lR вр.н) = 140 b 2/(lh),
bh 2 lR вр.н) = 140 b 2/(lh), и
и  для прямолинейной полосы с непрерывным шарнирным подкреплением вдоль растянутой кромки выражаются формулами
для прямолинейной полосы с непрерывным шарнирным подкреплением вдоль растянутой кромки выражаются формулами , (32)
, (32) - некоторая функция числа подкреплений m; причем
- некоторая функция числа подкреплений m; причем  (34)
(34)





 + [ M д/
+ [ M д/ 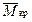 ] n ≤ 1, (35)
] n ≤ 1, (35)


