ББК 32.973 10 страница
В традиционных языках программирования значениями логических переменных считаются пары (ИСТИНА, ЛОЖЬ) или (1, 0). С эргономической точки зрения, такой подход нельзя признать удачным. В самом деле, использование “шибко мудреных” слов ИСТИНА и ЛОЖЬ или Чтобы поправить дело, в качестве значений логических переменных и логических функций гораздо лучше выбрать простые и ясные слова “да” и “нет”, семантика которых не требует пояснений и понятна даже ребенку. Исходя из этого, в языке ДРАКОН логические функции, переменные и выражения рассматриваются как да-нетные вопросы. Логическая функция И определяется как функция, которая принимает значение
 57 57
 60 60
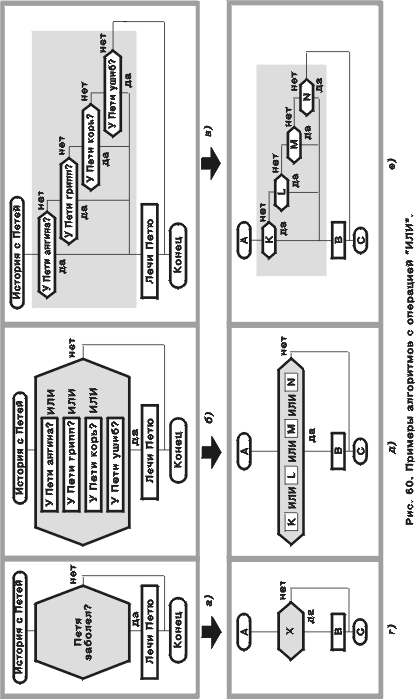
“да”, если все логические переменные имеют значение “да”. В остальных случаях функция приобретает значение “нет” (рис. 55)[17]. Существуют два способа изображения функции И на языке ДРАКОН: текстовый и визуальный. В первом случае используют одну икону “вопрос”, внутри которой пишут логическое выражение, состоящее из логических переменных, соединенных знаками логической операции И (рис. 56 слева). В другом случае на одной вертикали рисуют N икон “вопрос”, где N — число логических переменных, причем в каждой иконе записывают одну логическую переменную (рис. 56 справа). Визуальная формула на рис. 56 показывает, что оба способа эквивалентны. Примеры на рис. 57 подтверждают это. Для практического использования рекомендуется визуальный способ, так как он более нагляден и позволяет быстрее найти ошибку в сложном алгоритме. Следует подчеркнуть, что текстовый способ не является запрещенным, но пользоваться им следует с осторожностью и лишь в тех случаях, когда пользователь убежден в своих способностях гарантировать отсутствие ошибок. Опыт показывает, что большинство людей выбирает визуальный способ как более легкий. Однако подготовленные специалисты, знакомые с основами математической логики, иногда предпочитают текстовый метод. Таким людям можно посоветовать освоить оба метода. ВИЗУАЛИЗАЦИЯ ФУНКЦИИ ИЛИ Логическая функция ИЛИ принимает значение “да”, если хотя бы одна логическая переменная имеет значение “да”. Функция принимает значение “нет”, если все логические переменные имеют значение “нет” (рис. 58). На языке ДРАКОН функцию ИЛИ можно записать двумя способами. Если выбран текстовый способ, рисуют одну икону “вопрос”, содержащую логическое выражение (рис. 59 слева). При визуальном способе используют несколько икон “вопрос”, у которых объединяют нижний выход; в каждой иконе пишут одну логическую переменную (рис. 59 справа). Из рис. 59 и 60 видно, что оба метода эквивалентны. ВИЗУАЛИЗАЦИЯ ФУНКЦИИ НЕ Функция W = если Z = да, то W = нет; если Z = нет, то W = да.
Визуальные формулы на рис. 61 показывают, что знак логического отрицания можно исключить из дракон-схемы, если поменять местами слова “да” и “нет” на выходах иконы “вопрос” (при этом иконы, находящиеся в плечах развилки, следует оставить на своих местах). Упражнения на рис. 62—66 помогут читателю закрепить материал. ВИЗУАЛИЗАЦИЯ СЛОЖНЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ Рассмотрим функцию
На рис. 67 показан визуальный способ записи этой функции. Из рисунка видно, что формула (1) разбивается на три части: 1) А и Функция А и В формуле (1) некоторые члены записаны без логического отрицания (А, В, D, Е), другие — с отрицанием ( Изложенные соображения позволяют сформулировать две теоремы. Теорема 1. Дракон-схему, содержащую логические связки И, ИЛИ, НЕ внутри икон “вопрос”, всегда можно преобразовать в эквивалентную дракон-схему, не содержащую указанных связок. Теорема 2. Если некоторый фрагмент дракон-схемы имеет один вход, два выхода и содержит только иконы “вопрос”, причем первый выход вычисляет функцию X, то второй выход вычисляет ее логическое отрицание Доказательство теорем предоставляем читателю. ВЫВОДЫ 1. В алгоритмах со сложной логикой часто используются условные операторы с логическими выражениями. Опыт показывает, что такие операторы во многих случаях трудны для понимания, что нередко приводит к ошибкам. 2. В языке ДРАКОН используются визуальные логические выражения, позволяющие при желании полностью исключить логические связки И, ИЛИ, НЕ из условных операторов. 3. Визуализация логических формул во многих практически важных случаях заметно облегчает их понимание и уменьшает вероятность ошибок. Г Л А В А 10 Что такое эргономичный текст? Все в алгоритме понятно и ясно, МОЖНО ЛИ СДЕЛАТЬ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ Одна из основных целей языка ДРАКОН — улучшение понимаемости алгоритмов, программ и технологий. До сих пор мы решали эту задачу методом визуализации, превращая часть текста в эргономичный графический образ. А как должна выглядеть другая часть текста — та, что не подлежит визуализации и записывается внутри икон? Как изменить эргономические характеристики текстовых надписей на дракон-схемах, чтобы в максимальной степени улучшить их понимаемость? Поставленный вопрос слишком обширен и сложен. Поэтому сузим тему и ограничимся частной задачей: как следует записывать идентификаторы логических переменных и логические выражения, чтобы сделать их более понятными? Для обсуждения темы лучше всего подходят формальные идентификаторы и формальные логические выражения. Это значит, что визуальный псевдоязык ДРАКОН-1 для указанной цели не годится, так как его текстовый синтаксис неформальный. По этой причине материал настоящей главы опирается на идеи визуального языка программирования ДРАКОН-2, у которого обе части синтаксиса (и визуальная, и текстовая) являются строго формальными. Таким образом, в данной главе мы впервые коснемся вопроса о программировании на языке ДРАКОН. Точнее говоря, речь пойдет об одном частном вопросе программирования, касающемся правил записи логических выражений. ПРИМЕР ДЛЯ ИССЛЕДОВАНИЯ ЭРГОНОМИЧНОСТИ Итак, мы собираемся найти эргономичный способ записи сложных логических выражений. Чтобы разобраться в сути вопроса, желательно иметь под рукой какой-нибудь пример, на котором мы будем “проигрывать” различные методы улучшения эргономичности. Предположим, нужно создать алгоритм, управляющий автомобилем-роботом, проезжающим через перекресток со светофором в условиях реального уличного движения. Примем соглашение, что автомобиль-робот движется только по прямой, и выберем самый простой алгоритм управления (рис. 75). Логический признак, разрешающий (или запрещающий) роботу ехать вперед, имеет идентификатор “Можно.ехать.через.перекресток”. Будем считать, что данный признак принимает значение “да” в трех случаях: ! горит зеленый сигнал светофора и нет помех движению; ! желтый сигнал загорелся, когда робот уже выехал на перекресток, и нет помех движению; ! светофор сломался (нет ни зеленого, ни желтого, ни красного сигнала) и нет помех движению. В остальных случаях признак имеет значение “нет”, запрещающее роботу движение через перекресток. Введем обозначения, показанные на рис. 76, которым соответствуют очевидные равенства: Y = Можно.ехать.через.перекресток (1) А = Зеленый.сигнал.светофора (2) В = Желтый.сигнал.светофора (3) С = Красный.сигнал.светофора (4) D = Робот.выехал.на.перекресток (5) Е = Помехи.для.движения (6) Если принять указанные условия и обозначения, логическая функция Y задается формулой Y = (A & ┐ E) Пример, представленный на рис. 75 и 76, позволяет приступить к изучению проблемы. Ниже мы рассмотрим несколько вариантов записи логических выражений и сравним их между собой с эргономической точки зрения. При этом предполагается, что робот имеет пять датчиков, формирующих логические сигналы А, В, С, D, E, которые поступают в бортовой компьютер, управляющий движением робота. ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ Произведем эквивалентное преобразование алгоритма на рис. 75. Учитывая равенство (1) заменим идентификатор “Можно.ехать.через. перекресток” буквой Y, после чего вместо Y подставим логическое выражение из формулы (7). В результате получим алгоритм на рис. 77. Некоторые математики скорее всего похвалят этот алгоритм. Они, возможно, скажут, что с математической точки зрения выражение в иконе “вопрос” является компактным, лаконичным, изящным и обозримым[18].
К сожалению, подобная позиция не учитывает эргономических соображений и является устаревшей. Сразу оговоримся: речь, разумеется, идет не о том, чтобы заменить математику эргономикой, а всего лишь о том, чтобы, сохраняя математическую строгость в неприкосновенности, решительно отказаться от эргономической беспечности традиционных математических построений. Это означает, что однобокий математический подход должен уступить место системному подходу, в котором органически сочетаются математические и эргономические методы. Для обозначения нового подхода можно предложить термин “когнитивная формализация знаний”. Сделаем еще одну оговорку. Формула (7) была бы вполне приемлемой, если бы речь шла об абстрактной задаче, цель которой — выявить математическую сущность проблемы. Однако в данном случае речь идет о прикладной задаче — создании программы управления автомобилем-роботом. Недостаток формулы (7) и алгоритма на рис. 77 состоит в том, что идентификаторы А, В, С, D, Е не смысловые, а абстрактные. Они оставляют наши знания о предметной области за пределами программного текста. Чем это плохо? Вспомним, что сегодня критической проблемой являются не машинные, а человеческие ресурсы, причем экономия последних теснейшим образом связана с проблемой понимания, которая превращается в центральную проблему информатики. Производительность труда при создании информационных систем и систем управления напрямую зависит от успешного решения проблемы понимания, обеспечивающего быструю и безошибочную разработку алгоритмов и программ. Это общее положение тесно связано с обсуждаемым вопросом. В самом деле, люди, которые прекрасно знают прикладную задачу и предметную область, но не знают или забыли обозначения (1)—(6), например заказчики, постановщики задач, комплексники и т. д., воспринимают идентификаторы А, В, С, D, Е и составленные из них формулы как бессмысленный набор символов. Следовательно, эти люди лишаются возможности принять участие в проверке правильности алгоритмов и программ и внести свой вклад в устранение ошибок. Чтобы обнаружить ошибку в логическом выражении, необходимо хорошо понимать его смысл. Чтобы уяснить суть логического выражения на рис. 77, человек вынужден помнить не только смысловые понятия, но и абстрактные идентификаторы, твердо знать соответствие между ними. Это создает двойную нагрузку на память человека (алгоритмиста, программиста и т. д.), порождает дополнительные и ничем не обоснованные трудности при поиске и выявлении ошибок. Для большинства специалистов, знающих прикладную задачу, логическое выражение на рис. 77 не дает никакой подсказки о семантике логических переменных и фактически представляет собой загадочный ребус. Оно служит типичным примером эргономической неряшливости традиционных методов математического описания прикладных задач. Отсюда проистекает вывод: в прикладных задачах использование абстрактных идентификаторов в логических выражениях эргономически недопустимо. ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ Абстрактные идентификаторы использовались на первом этапе развития программирования. Сегодня в прикладных программах они встречаются гораздо реже, уступив место так называемым мнемоническим именам, т. е. коротким смысловым идентификаторам, которые в большинстве случаев имеют длину до восьми символов. Преобладание восьмисимвольных идентификаторов характерно для второго этапа развития языков программирования. Вот типичная рекомендация этого периода: “не оправдано применение имен, подобных Х или I, тогда как имена МАХ или NEXT передают смысл гораздо точнее”. Последуем совету и, продолжая наш пример с автомобилем-роботом, заменим абстрактные идентификаторы на мнемонические имена согласно табл. 2. Таблица 2
На рис. 78 показан алгоритм, полученный в результате такой замены. Можно ли назвать логическое выражение на рис. 78 эргономичным? Очевидно, что мнемонические имена лучше абстрактных. Они были придуманы с благородной целью — облегчить запоминание понятий, чтобы формальное имя создавало намек на содержательную сторону дела. Увы! Говорить намеками — вовсе не значит говорить понятно. Причина неудачи в том, что длина идентификатора восемь символов слишком мала и явно недостаточна для хорошего, ясного и доходчивого описания сложных понятий. Поэтому при создании восьмисимвольных идентификаторов приходится экономить каждый символ и часто использовать невразумительные слова-обрубки, такие, как Зелсиг (зеленый сигнал светофора), Красиг, Желсиг и т. д. В самом деле, глядя на идентификатор “Робнапер” (рис. 78) мало кто догадается, что речь идет о признаке “Робот.выехал.на.перекресток”. Сравнивая логические выражения на рис. 77 и 78, можно сказать, что в последнем случае понимаемость алгоритма, если и увеличилась, то ненамного. Таким образом, восьмисимвольные смысловые идентификаторы не могут обеспечить требуемое улучшение эргономических характеристик логических выражений. ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ Для третьего этапа развития языков программирования, который начался сравнительно недавно, характерен переход к длинным смысловым идентификаторам, содержащим до 32 символов. Здесь необходимо уточнение. Некоторые трансляторы делят идентификаторы на две части, обрабатывая только первую часть и игнорируя вторую. В результате разные идентификаторы, имеющие различие в последних символах, рассматриваются транслятором как тождественные. Такие случаи мы исключаем из рассмотрения. При дальнейшем изложении подразумевается, что все инструментальные программы, включая транслятор, обеспечивают необходимую программную обработку всех 32 символов идентификатора. Увеличение длины идентификатора до 32 символов позволяет получить два важных эргономических преимущества. Во-первых, во многих (хотя и не во всех) случаях появляется возможность отказаться от сокращений и использовать полные слова. Во-вторых, для разграничения слов, входящих в состав идентификатора, можно ввести эргономичные разделители, например точку или нижнюю черту. Пример логического выражения, в котором используются идентификаторы с точками-разделителями и полными (несокращенными) словами, представлен на рис. 79. Легко видеть, что оно обладает более высокой понимаемостью, чем предыдущие примеры. Тем не менее здесь есть одно “но”. ВАЖНЫЙ МОМЕНТ, На рис. 75 записан вопрос “Можно.ехать.через.перекресток”, который объясняет принцип разветвления алгоритма: при ответе “да” выполняется команда “Ехать.вперед”, при ответе “нет” действия отсутствуют. Данный вопрос играет ключевую роль: если его удалить, алгоритм становится непонятным. В связи с этим целесообразно ввести понятие главный вопрос условного оператора. А теперь взглянем на рис. 77—79. Нетрудно заметить, что в иконе “вопрос” записана масса любопытных подробностей, однако интересующий нас вопрос отсутствует. Он бесследно исчез. Таким образом, логические выражения на рис. 77—79 имеют общий недостаток, причем весьма существенный. В них нет главного вопроса, нет ключа, объясняющего сущность алгоритма. Налицо парадокс: логические выражения не дают явной информации о том, на какой именно вопрос мы отвечаем “да” или “нет”. Более того, они не позволяют читателю легко и быстро восстановить формулировку главного вопроса и не стимулируют у него стремления к получению подобной информации. Не будет преувеличением сказать, что перечисленные логические выражения затуманивают суть дела, поскольку отсутствие главного вопроса ничем нельзя компенсировать. В итоге алгоритмы на рис. 77—79 оказываются непонятными и эргономически неприемлемыми. Отсюда вытекает, что использование эргономически правильных длинных смысловых идентификаторов является необходимым, но отнюдь не достаточным условием для построения эргономичного логического текста. КАК ПРИСВОИТЬ ЗНАЧЕНИЕ ЛОГИЧЕСКОЙ Мы уже говорили, что в традиционных языках для значений логических переменных используют слова TRUE и FALSE, ИСТИНА и ЛОЖЬ, 1 и 0. Однако логико-эргономические исследования показывают, что указанные обозначения являются избыточными и могут быть безболезненно и с пользой для дела исключены из программных текстов. Стремление “уничтожить” лишние обозначения объясняется эргономическими причинами, так как все ненужные записи являются визуальными помехами, которые засоряют текст программы и путают читателя. Язык ДРАКОН позволяет решить задачу двумя способами. В первом случае применяется икона “действие”, внутри которой записывается оператор присваивания (рис. 80). Визуальный оператор на рис. 80 означает, что идентификатору “Можно.ехать.через.перекресток” присваивается некоторое значение. Какое именно? Для этого нужно вычислить рамочное логическое выражение, записанное в трех рамках, соединенных знаками ИЛИ. Результатом вычисления будет “1” или “0”. Таким образом, цель достигнута, хотя обозначения “1” и “0” в программном тексте отсутствуют.
Во втором случае используется икона “полка” (рис. 1, икона И10), на верхнем этаже которой пишут зарезервированное предложение “Установить признак” или “Снять признак”. На нижнем этаже указывают идентификатор признака. Операторы языка ДРАКОН означают, что логической переменной “Норма.насоса” присваивается значение “1” и “0” соответственно. Еще один пример использования иконы “полка” показан на рис. 81. Легко видеть, что на рис. 81 используется та же хитрость, что и на рис. 80, а именно: логической переменной присваивается значение “1” или “0”, хотя обозначения “1” и “0” в тексте программы нигде не встречаются! ПРАВИЛА ЗАПИСИ Увеличение длины идентификаторов приводит к тому, что традиционная горизонтальная запись логических выражений становится невозможной. В связи с этим применяется вертикальная запись, пример которой показан на рис. 80. Вертикальный логический текст на языке ДРАКОН пишут в соответствии со следующими правилами. ! В иконе “действие” размещают один оператор присваивания. ! В верхней строке пишут идентификатор логической переменной и знак присваивания. ! Ниже пишут логическое выражение, причем каждая конъюнкция заключается в прямоугольную рамку. ! Для операций И, ИЛИ, НЕ используют обозначения &, ИЛИ, ┐соответственно. ! Используют идентификаторы длиной до 32 символов. ! Первые символы всех идентификаторов располагают на одной вертикали. ! Знак отрицания ┐пишут слева от идентификатора. ! Все знаки отрицания (если они есть) помещают на одной вертикали. ! Знаки конъюнкции & записывают справа от идентификатора. ! Все знаки конъюнкции пишут на одной вертикали. ! Вертикальные линии рамок располагают на одной вертикали. ! Знаки = и ИЛИ помещают на одной вертикали. КАК ПОСТРОИТЬ ЭРГОНОМИЧНЫЙ ЛОГИЧЕСКИЙ ТЕКСТ? Ранее мы пришли к выводу, что алгоритм на рис. 79 является эргономически неудачным. Каким образом можно его исправить? Вопрос отнюдь не простой. По-видимому, в разных ситуациях он может приводить к разным ответам. В связи с этим изложенные ниже соображения и советы имеют не обязательный, а всего лишь рекомендательный характер. Их нужно рассматривать как один из возможных способов решения проблемы. ! В иконе “вопрос” не следует записывать логическое выражение, в особенности сложное. Вместо него рекомендуется поместить один-единственный идентификатор, содержащий ясную и четкую словесную формулировку главного вопроса. ! В общем случае указанный идентификатор может оказаться неопределенным. Чтобы исключить эту неприятность, необходимо заблаговременно присвоить ему нужное значение. Для этого существуют два метода: рамочный и визуальный. ! В рамочном методе используется рамочное логическое выражение, записанное в иконе “действие”. Производится вычисление рамочного выражения, результат присваивается идентификатору главного вопроса (рис. 80). ! В визуальном методе применяется визуальное логическое выражение и два оператора “Установить признак” и “Снять признак”, записанные в иконах “полка”.
|




 называется функцией НЕ, если логические переменные Z и W принимают инверсные значения, т. е. удовлетворяют условиям:
называется функцией НЕ, если логические переменные Z и W принимают инверсные значения, т. е. удовлетворяют условиям:



 и C) или (D и E и
и C) или (D и E и 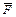 )
)
 (рис. 67—73).
(рис. 67—73). (B & D & ┐ E)
(B & D & ┐ E) 




