ББК 32.973 19 страница
Обобщая вышеизложенное, можно сделать ряд замечаний. ! Способность или неспособность человечества решать жизненно важные глобальные, локальные и иные проблемы прямо зависит от эффективности всемирного разума и его локальных компонентов, от качества средств представления и формализации знаний, языковых средств понимания и взаимопонимания, удовлетворяющих критерию сверхвысокого понимания, эргономическому критерию Декарта. ! Чернобыль и другие инциденты со всей ясностью обнажили беспомощность нынешних форм планетарного интеллекта и поставили вопрос о разработке нового поколения интеллектуальных средств — суперязыков, способных обеспечить качественно новый уровень человеческого ума. ! Традиционные технократические методы разработки крупномасштабных промышленных объектов и социальных нововведений полностью исчерпали свои возможности, устарели и должны уступить место новым социотехническим методам, которые подразумевают системный подход к проектированию социосферы, техносферы и гарантоспособной человеческой деятельности. ВЫВОДЫ 1. Языки программирования играют заметную роль в человеческой культуре, являясь составным элементом компьютерной революции, которая, в свою очередь, есть необходимое условие перехода к информационному обществу. Наряду с этим все больше ощущается потребность в суперязыках, которые предназначены для кардинального улучшения работы ума, облегчения понимания и взаимопонимания, обеспечения более эффективного интеллектуального взаимодействия между людьми и в конечном итоге — улучшения человеческой деятельности (как теоретической, так и практической). 2. Некоторые суперязыки могут выполнять функции языков программирования, другие — нет. В роли суперязыков могут выступать только эргономичные визуальные языки. 3. Проблема создания суперязыков приобрела особую актуальность в последнее время, когда выявилась жесткая связь между интеллектом и выживанием и несостоятельность традиционных методов интеллектуальной работы.
5. Суперязыки должны сделать то, чего не могут языки программирования: стимулировать стратегический интеллектуальный прорыв, в максимально возможной степени увеличить умственную мощь человечества, обеспечить качественно новый уровень понимания и взаимопонимания и на этой основе — гарантоспособность планетарной и локальной человеческой деятельности. 6. Первым и, к сожалению, пока единственным примером суперязыка является техноязык ДРАКОН. Создание остальных суперязыков — дело будущего. Возможно, они будут появляться в результате эволюции (в сторону большей наглядности, доступности и общезначимости) графических языков новейших модификаций методологии RAD и CASE -технологий. Возможны и другие варианты. ДРАКОН — это всего лишь начальное звено в цепи суперязыков, которая обязательно должна наращиваться. 7. Язык ДРАКОН — это первый сознательно сделанный эргономический шаг в языковом строительстве. Эргономический — значит, во-первых, нацеленный на улучшение работы ума, во-вторых, опирающийся на всю мощь науки о человеческих факторах — эргономики и когнитивной науки. Сказанное можно резюмировать в форме краткого лозунга: ДРАКОН — это эргономическая революция в “языкостроении”. 8. Использование эргономики в языкостроении открывает перед этой наукой новые вдохновляющие перспективы, выявляет недостаточность нынешнего уровня эргономических знаний и требует дальнейшего развития ее идей. 9. Использование ДРАКОНА в качестве стандарта для описания структуры деятельности (как человеческой, так и делегированной) рассматривается как пробный шаг в направлении решения важнейшей цивилизационной задачи — проектирования гарантоспособной деятельности.
Г Л А В А 19 Возможна ли эргономизация Ученый, ты объясняешь нам науку, но кто объяснит нам твое объяснение? Джордж Байрон ПОЧЕМУ ДЖОН ФОН НЕЙМАН ПРОВАЛИЛСЯ Математика — одна из разновидностей человеческой деятельности, поэтому логично поставить вопрос об эргономизации математики. Актуальность этой проблемы определяется следующим. Современная наука и система образования немыслимы без математики, но, к сожалению, математика чрезвычайно трудна и продолжает усложняться. Изучение математики требует колоссальных трудозатрат. Однако речь не только об учащихся. Появляющееся новое математическое знание стало столь разветвленным, что охватить его одному человеку или даже коллективу единомышленников (например, известной группе Николас Бурбаки) “физически невозможно”. Даже великий Джон фон Нейман признавался, что знает не больше чем 1/3корпуса математики и, чтобы проверить себя, попросил С. Улама проэкзаменовать его. Тот вспоминает: “Я устроил ему некоторое подобие докторантского экзамена в различных областях, стараясь выделить те вопросы, на которые он не мог бы ответить. Я нашел пробелы в дифференциальной геометрии, теории чисел, алгебре, где его ответы были неудовлетворительными” [1]. А ведь фон Нейман был выдающимся математиком! Но если трудности испытывают фигуры такого масштаба, с какими же поистине невероятными трудностями сталкивается подавляющее большинство математиков? Недаром говорят, что “в условиях современной математики математик не знает, как это ни парадоксально, математики” [1]. Что же тогда можно сказать о математических знаниях нематематиков и многочисленных армиях студентов? Проблема в том, что для большинства нематематических специальностей требования к математической подготовке постоянно возрастают, поскольку возрастает роль математики в современной науке и технике, теории и практике. В итоге получается, что люди не обладают знаниями, которые необходимы им для эффективного выполнения профессиональных обязанностей. Отпугивающая многих трудность изучения математики и вызванный ею недобор математических знаний неизбежно приводит к снижению интеллектуального потенциала общества, еще более усугубляя интеллектуальный кризис цивилизации. Попытка “запихнуть” в человеческую голову больше, чем она способна переварить за известный промежуток времени, ведет к экстенсификации учебного процесса, перегрузкам учащихся и педагогов, низкой эффективности обучения. Получается замкнутый круг, из которого в рамках традиционных подходов фактически нет выхода. СУЩЕСТВУЕТ ЛИ ПРОПАСТЬ Чтобы преодолеть или хотя бы ослабить названные трудности, необходимо: ! улучшить понимаемость (когнитивное качество) математической литературы и за счет этого облегчить изучение математики; ! улучшить взаимопонимание между специалистами, работающими в разных отраслях и отделах математики (а их свыше трех тысяч [1]), а также в прикладных областях, тесно с нею связанных; ! уменьшить интеллектуальные усилия (интегральные умственные трудозатраты), которые общество расходует на изучение и решение математических проблем (при сохранении заданных стандартов качества). Легко сообразить, что перечисленные задачи имеют эргономический характер. При разработке принципов эргономизации математики полезно учесть мировой опыт развития и комбинирования математической символики от древнейших времен до наших дней, но самое главное, уяснить, что эргономизация не есть нечто внешнее по отношению к математике. Как раз наоборот, эргономизация — это неотъемлемая внутренняя компонента исторического процесса развития математических идей. Тем не менее остается фактом, что сегодня эргономика и математика почти не имеют точек соприкосновения (применение математических методов в эргономике не в счет). Их разделяет пропасть взаимного непонимания. Другой удивительный факт состоит в том, что математики на протяжении всей истории применяли и применяют эргономические методы. Однако этот процесс носил и носит неосознанный, стихийный и кустарный характер, ощутимо снижая когнитивное качество математических текстов, ухудшая понимание и взаимопонимание в математическом сообществе. Грубо говоря, эргономическая беспечность (а если отбросить деликатность — эргономическая неграмотность) традиционных математических методов представляет собой одну из причин неоправданно высокого интеллектуального барьера, окружающего величественный дворец математической науки. Для обозначения этого барьера появился даже специальный термин — математический терроризм [2]. Мы исходим из того, что в наш междисциплинарный век пренебрежение к эргономическим методам следует признать устаревшим. К тому же оно вступает в противоречие с уроками истории. Чтобы сделать эту мысль более наглядной, проиллюстрируем ее на примере развития правил записи алгебраических уравнений, выбрав в качестве точки отсчета алгебру Диофанта. АЛГЕБРА ДИОФАНТА Греческий математик Диофант (III век нашей эры) был последним великим математиком античности. До него уравнения решались в словесной либо в геометрической форме. Он впервые использовал в алгебре буквенную символику. Но введенные им буквенные обозначения были сокращениями соответствующих математических терминов, а не алгебраическими символами в нашем понимании. Тем не менее новшества Диофанта имели революционный характер. Он ввел обозначения неизвестной величины, ее первых шести положительных и отрицательных степеней, отрицательные числа, знак “минус” и знак “равенство”. Благодаря этому Диофанту удалось получить ряд важных результатов. Он даже сумел предвосхитить подстановки Эйлера [3, 4]. Однако современному читателю символика Диофанта кажется странной, запутанной и очень непривычной. Попробуем запастись терпением и совершим небольшую прогулку по джунглям диофантовой алгебры, ограничившись одним-единственным вопросом: как Диофант записывал уравнения? Прежде всего, попытаемся выяснить: как будут выглядеть наши современные знаки
если их перевести на язык Диофанта? Ответ дает табл. 8. Таблица 8
Таблица 9
Для обозначения чисел Диофант использует общепринятую у греков символику [5] (табл. 9). Греческие числа образуют непозиционную десятичную систему: как
При записи свободного члена уравнения Диофант сначала ставит символ М° (признак свободного члена), а затем его числовое значение (табл. 11). Таблица 10
Таблица 11
С учетом сказанного приведем несколько примеров записи уравнений в символике Диофанта. Обратите внимание: чтобы избавиться от нуля, во втором и третьем примерах Диофанту пришлось перенести свободный член в правую часть уравнения (табл. 12). Таблица 12
ЭРГОНОМИЧЕСКИЙ АНАЛИЗ АЛГЕБРЫ ДИОФАНТА Попытаемся оценить способ записи уравнений, использованный Диофантом, с точки зрения современных когнитивных представлений. Не претендуя на составление полной “дефектной ведомости”, укажем лишь несколько эргономических недостатков диофантовой алгебры. 1. Когда человек смотрит на запись уравнения, он должен решить несколько визуальных задач, обеспечивающих правильное зрительное восприятие и понимание сути дела, причем сделать это “без излишней траты умственных сил”. Первая задача — разбить зрительную сцену на два главных смысловых блока (левую и правую части уравнения). Для этого нужно выполнить три зрительных операции: ! бегло просмотрев все символы уравнения, найти среди них знак равенства; ! сделать вывод: зрительная зона, находящаяся левее этого знака, есть левая часть уравнения; ! сделать вывод: зона, лежащая правее, есть правая часть. Современный знак равенства “=” с пробелами до и после него имеет удачную эргономическую конфигурацию, как нельзя лучше подходящую для этой цели. По форме он резко отличается от других знаков и эффектно “разламывает” уравнение на две части, благодаря чему человеческий глаз моментально решает первую визуальную задачу. Что касается алгебры Диофанта, то греческая буква иота i, используемая как знак равенства, слишком невзрачна и невыразительна — она теряется среди других букв. Из-за этого зрительное выделение и опознание двух частей равенства заметно усложняется.
В самом деле, современное выражение х 2 + 3 х по Диофанту записывается так:
В последней формуле присутствуют три пары из двух смежных букв. Все они трактуются по-разному, что создает неоправданную нагрузку на память человека: ! запись ! запись ! запись Столь сложные правила расшифровки зрительной сцены вносят дополнительные и никому не нужные трудности в процесс зрительного восприятия. 3. Три класса объектов (неизвестные, цифры и операции) имеют сходные обозначения (всюду — буквы), что затрудняет визуальное различение указанных классов и кристаллизацию соответствующих понятий. 4. Не существует обозначений для нуля, плюса и степеней неизвестной выше шестой. 5. Степени неизвестной величины обозначаются не путем вариации одного знака (x, x 2, x 3, x 4, x 5, x 6), но имеют неоправданные различия и отсутствие общих элементов. В итоге нет визуальной подсказки, облегчающей опознание и выявление “родственных черт” у сходных понятий (степеней). 6. Отсутствует единая символика для чисел и показателей степени. Например, цифра 3 обозначается через Проведенный анализ показывает, что по эргономическим показателям символика Диофанта значительно уступает современным обозначениям. ЭРГОНОМИЗАЦИЯ АЛГЕБРЫ Алгебра Диофанта для своего времени была крупнейшим достижением. Однако ее постигла печальная участь. Оригинал на греческом языке в Европе был утерян и вновь найден только в XV веке [4]. К счастью, идеи Диофанта получили распространение в арабском мире и вернулись в Европу кружным путем — через арабское культурное влияние. При этом многое было утеряно и переоткрыто заново. Важным этапом на пути эргономизации европейской алгебры была замена греческих цифр на арабские. Самый древний европейский манускрипт, содержащий эти десять цифр, — “Вигиланский кодекс”, написанный в Испании в 976 г. Однако по ряду причин, которых мы не касаемся, арабская система счисления распространялась в Европе очень медленно и стала общепринятой лишь к 1500 г. [6]. К сожалению, имело место и попятное движение. Целый ряд эргономических находок Диофанта на несколько столетий был забыт. В частности, оказалась утраченной его буквенная символика, уступившая место словесным описаниям. Например, Леонардо Пизанский (1180—1240) называет неизвестную res (вещь) или radix (корень), квадрат неизвестной — census (имущество) или quadratus (квадрат); данное число — numerus. Все это — латинские переводы соответствующих арабских слов [6]. Наваждение слов преследовало математиков многие века. Поскольку не существовало символов даже для самых простых арифметических действий, каждый автор по-своему записывал сложение и вычитание, возведение в степень и извлечение корня. Требовалось немало усилий, чтобы разобраться в таком сложном переплетении форм записи. Поэтому ученые доверяли больше словам, чем знакам, тяготели больше к словесным описаниям, чем к формулам. Однако мало-помалу формульная запись начала пробивать себе дорогу. Но, Боже, что это были за формулы! Например, уравнение
|


 4. Выяснилось также, что языки программирования не могут обеспечить требуемый прирост интеллектуальной силы человеческих коллективов (локальных и глобальных). Из-за своего кастового характера и узости социальной базы языки программирования очень слабо влияют на улучшение коллективной работы ума в масштабах общества, на рост могущества социального интеллекта. Фактически они продемонстрировали свою непригодность для решения этой задачи.
4. Выяснилось также, что языки программирования не могут обеспечить требуемый прирост интеллектуальной силы человеческих коллективов (локальных и глобальных). Из-за своего кастового характера и узости социальной базы языки программирования очень слабо влияют на улучшение коллективной работы ума в масштабах общества, на рост могущества социального интеллекта. Фактически они продемонстрировали свою непригодность для решения этой задачи. ,
,




























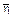

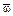




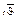
 , так и
, так и  может значить только 14. Отсутствие позиционной системы вносит большие когнитивные затруднения: задача 4 × 10 = 40 (
может значить только 14. Отсутствие позиционной системы вносит большие когнитивные затруднения: задача 4 × 10 = 40 ( ) у греков не имеет ничего общего с “родственной” задачей
) у греков не имеет ничего общего с “родственной” задачей ). По этому поводу немецкий психолог Фридхарт Кликс восклицает: “Насколько проще метод нашей позиционной системы, насколько меньше затрат при решении одинаковых задач!” [5].
). По этому поводу немецкий психолог Фридхарт Кликс восклицает: “Насколько проще метод нашей позиционной системы, насколько меньше затрат при решении одинаковых задач!” [5]. Каждый член уравнения Диофант пишет так: сначала указывается степень неизвестного, потом числовой коэффициент; перед отрицательными членами ставится знак недостатка (по-нашему, минус), перед положительным — ничего (плюсом Диофант не пользуется) (табл. 10).
Каждый член уравнения Диофант пишет так: сначала указывается степень неизвестного, потом числовой коэффициент; перед отрицательными членами ставится знак недостатка (по-нашему, минус), перед положительным — ничего (плюсом Диофант не пользуется) (табл. 10).
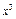








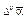


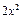




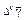


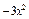



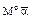



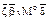











 обозначает х 2;
обозначает х 2; обозначает операцию сложения, причем в записи складываются члены
обозначает операцию сложения, причем в записи складываются члены  ;
; обозначает умножение х ´ 3.
обозначает умножение х ´ 3. , а x 3— через
, а x 3— через 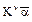 , но в последнем выражении цифра 3 отсутствует.
, но в последнем выражении цифра 3 отсутствует. записывалось в XV веке во Франции таким образом [7]:
записывалось в XV веке во Франции таким образом [7]:


