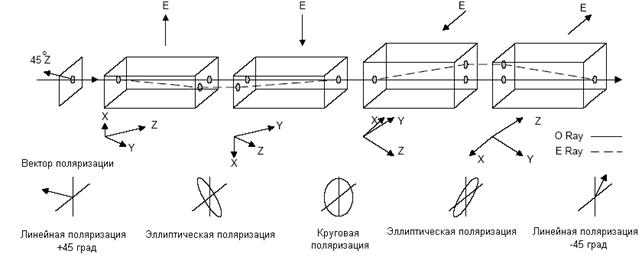
Электрооптический эффект
Линейная связь между электрической индукцией и полем
является приближенной. При сильных электрических полях, наблюдаются нелинейные соотношения, природа которых различна для различных материалов. В сильных полях диэлектрическая проницаемость является функцией приложенного электрического поля.
Это соотношение может быть представлено приближенно в виде ряда
или
где
для линейного эффекта. Коэффициенты Как уже говорилось, изменение показателя преломления под действием электрического поля называется электрооптическим эффектом. Симметрия кристалла определяющим образом влияет на характер электрооптического эффекта. Та для кристаллов, обладающих центром симметрии все Линейный электрооптический эффект можно наблюдать в кристаллах следующих точечных групп симметрии: триклинной кл. 1; монолинной кл. 2, m; ромбической кл. 3, 32, 3m; гексагональной кл. 6, 6mm, 622, В общем случае, для описания линейного электрооптического эффекта в кристаллах низшей симметрии необходимо 18 из 27 (благодаря симметрии компонент тензора третьего ранга относительно перестановки двух первых индексов) электрооптических коэффициентов. Вместо тензорной, часто используется матричная форма записи электрооптических коэффициентов.
i,j = 1,2,3; l = 1,...6 k = 1,2,3
При воздействии внешнего электрического поля на электрооптический кристалл в случае ЛЭФ можно записать уравнение (2.4) в следующем виде:
Принцип действия электрооптического модулятора
Фазовая задержка
поэтому
Таким образом для эффекта Поккельса фазовая задержка равна:
Принцип действия электрооптического модулятора основан на возникновении фазовой задержки под действием электрического поля. Так как фазовый сдвиг нормальных мод зависит от разности показателей преломления, то после прохождения в кристалле расстояния L волна претерпевает фазовый сдвиг, пропорциональный (в случае линейного эффекта) электрическому полю (2.9). При изменении поля Е во времени, фазовая задержка следует за изменением поля, если только скорость изменения поля Е не слишком высока. Т.о. электрооптический эффект приводит непосредственно к фазовой модуляции двух нормальных мод.
Устройство электрооптического модулятора по интенсивности схематически изображено на рис.2.4. Оно состоит из электрооптического элемента (3), помещенного между скрещенными поляризаторами (2,5), направление поляризации которых составляет угол 450 относительно главных осей эллипсоида, индуцированного электрическим полем (x’y’). На модулятор обычно накладывают смещающее напряжение После прохождения второго поляризатора - анализатора получается амплитудно модулированный сигнал (см. Рис.2.5). На этом рисунке П - плоскость поляризации первого поляризатора. А - плоскость поляризации второго поляризатора - анализатора. I,II - главные направления в кристалле. II
I0 = OP 2 I = (
I - интенсивность света прошедшего через анализатор.
I = I = Таким образом коэффициент пропускания модулятора
Если свет поляризован вдоль новой оси (x’ или y’), то электрическое поле не изменяет состояния поляризации, а меняет лишь фазу выходного сигнала.
Если смещающее электрическое поле синусоидальное
то поле Е падающего луча, которое на входной поверхности модулятора изменяется по закону
на выходе имеет вид:
величина
называется индексом фазовой модуляции. В зависимости от направления приложенного электрического поля относительно направления света различают два основных типа модуляции. 1. Модуляция называется продольной, если электрическое поле параллельно направлению распространения света. 2. Модуляция называется поперечной, если электрическое поле перпендикулярно направлению распространения волны.
2.2. Исследование электрооптических модуляторов света на основе кристалла 42 m (DKDP, ADP)
Уравнение индикатрисы. В отсутствие электрического поля кристалл DKDP, обладая структурой 42m, является одноосным кристаллом (рис.2.6). Поэтому у него существуют всего три не равных нулю электрооптических коэффициента:
Подставив их в (1.4), с учетом (2.4), получим уравнение индикатрисы показателей преломления этого кристалла:
При приложении электрического поля (Еx, Ey, Ez) форма индикатрисы и ориентация ее осей изменится, что приведет к изменению поляризации света, прошедшего через кристалл. У кристалла симметрии 42m (DKDP) величина
Приводя уравнение индикатрисы к главным осям x’, y’, которые, как видно из (2.16), повернуты относительно осей x’ и y’ на угол 450, получим
откуда видно, что у индикатрисы изменилась не только ориентация, но и форма (показатели преломления по осям x’ и y’). Новые показатели преломления будут:
Разность показателей преломления при распространении света в кристалле DKDP (рис.2.6) вдоль оси Y будет:
Функциональная схема В лабораторной установке использован электрооптический модулятор МЛ-102, в котором установлен кристалл DKDP симметрии 42m. Электрическое поле приложено к образцу перпендикулярно распространению света, т.е. модулятор является поперечным (рис.2.7). Т.к. поле приложено по оси Z, то в отсутствии поля анизотропия кристалла приводит к фазовому сдвигу пропорциональному длине кристалла:
При приложении поля индикатриса повернется на угол 450 и мы получим новые показатели преломления (2.18). Т.о. фазовый сдвиг
где
т.е.
Изменение показателей преломления Из (2.21) видно, что фазовый сдвиг
Расчет статической модуляционной характеристики (СМХ)
Рассмотрим схему электроптического модулятора по интенсивности (рис.2.9). Модулятор содержит источник излучения (Не- Ne лазер), поляризатор Р, электрооптический кристалл, анализатор и приемник излучения.
Под действием электрического поля Е изменяется фазовый сдвиг
где Таким образом, коэффициент пропускания зависит от управляемого параметра модулятора Из (2.22) видно, что наибольшее изменение 1)
2)
|

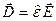
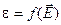 (2.2)
(2.2)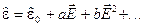 (2.3)
(2.3)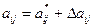 ,
, i,j,k= 1,2,3. (2.4)
i,j,k= 1,2,3. (2.4)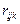 характеризуют изменение показателей преломления под действием приложенного электрического поля.
характеризуют изменение показателей преломления под действием приложенного электрического поля.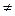 0 и наблюдается линейный электрооптический эффект (ЛЭФ) - эффект Поккельса.
0 и наблюдается линейный электрооптический эффект (ЛЭФ) - эффект Поккельса. ,
, 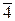 ,422, 4mm; кубической кл.
,422, 4mm; кубической кл. 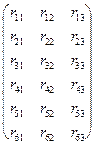
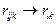
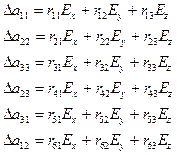 (2.6)
(2.6) ортогонально поляризованных лучей, проходящих через пластину толщиной d, вызываемая электрическим полем, определяется разностью показателей преломления обыкновенного и необыкновенного лучей:
ортогонально поляризованных лучей, проходящих через пластину толщиной d, вызываемая электрическим полем, определяется разностью показателей преломления обыкновенного и необыкновенного лучей: 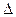 n = n’- n, n’ - показатель преломления кристалла при воздействии электрического поля Е.
n = n’- n, n’ - показатель преломления кристалла при воздействии электрического поля Е.  (2.7)
(2.7)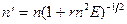 . Величина
. Величина 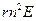 << 1,
<< 1,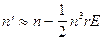 .
.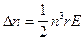 (2.8)
(2.8) . (2.9)
. (2.9)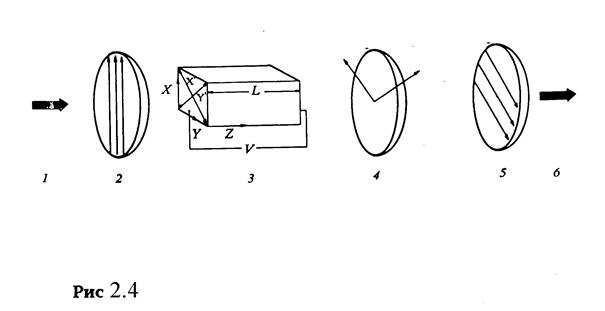
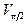 таким образом, чтобы создать фиксированную задержку
таким образом, чтобы создать фиксированную задержку 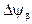 =
=  и добиться коэффициента пропускания 50%. Этого эффекта можно достичь так же помещая перед анализатором (А) соответствующим образом ориентированную двупреломляющую пластинку
и добиться коэффициента пропускания 50%. Этого эффекта можно достичь так же помещая перед анализатором (А) соответствующим образом ориентированную двупреломляющую пластинку 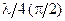 .
.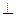 А, II-I = 450. ОР - амплитуда света после прохождения первого поляризатора.
А, II-I = 450. ОР - амплитуда света после прохождения первого поляризатора.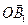 +
+ 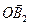 )2
)2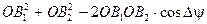 .
.
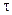 равен:
равен: (2.10)
(2.10)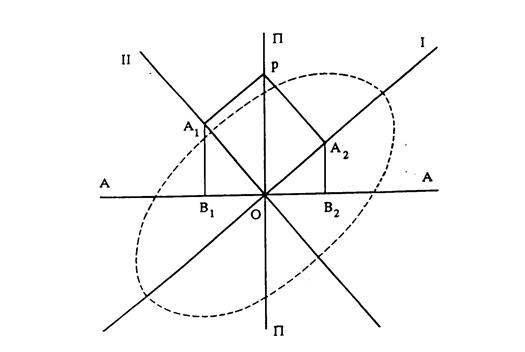
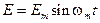 (2.11)
(2.11)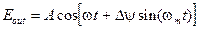 (2.13)
(2.13)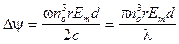 (2.14)
(2.14)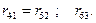
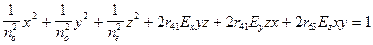 (2.15)
(2.15)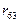 превышает
превышает 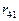 , поэтому при приложении поля вдоль оси Z (0,0,E), мы получим наибольшую величину электрооптического эффекта. С учетом приложенного поля уравнение (2.15) примет вид:
, поэтому при приложении поля вдоль оси Z (0,0,E), мы получим наибольшую величину электрооптического эффекта. С учетом приложенного поля уравнение (2.15) примет вид: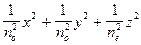
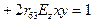 (2.16)
(2.16)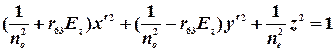 , (2.17)
, (2.17)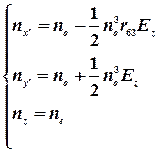 (2.18)
(2.18) Z
Z

 ne
ne
 no X
Y no
Рис. 2.6
no X
Y no
Рис. 2.6
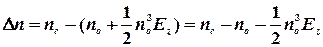 (2.19)
(2.19)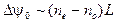 .
.









 Z E = (0,0,E)
Z E = (0,0,E)
 U
IВХ Y
X
Рис. 2.7
U
IВХ Y
X
Рис. 2.7
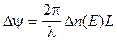 (2.20)
(2.20)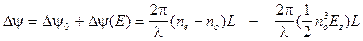
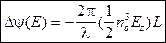 (2.21)
(2.21)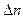 сильно зависит от температуры, поэтому для термокомпенсации первоначального фазового сдвига
сильно зависит от температуры, поэтому для термокомпенсации первоначального фазового сдвига  в модуляторе используют второй такой же кристалл, оси y и z которого ориентированы под углом 900 к осям x и z первого кристалла.
в модуляторе используют второй такой же кристалл, оси y и z которого ориентированы под углом 900 к осям x и z первого кристалла. Лазерное излучение, проходя поляризатор Р, поляризуется в плоскости РР’, повернутой на 450 относительно осей кристалла.
Лазерное излучение, проходя поляризатор Р, поляризуется в плоскости РР’, повернутой на 450 относительно осей кристалла.





















 P A
E а ПИ
P A
E а ПИ
 Р’
Р’ 
 IВХ IВЫХ
IВХ IВЫХ
 P
P  L a’
Рис. 2.9
L a’
Рис. 2.9
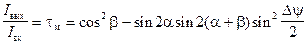 (2.22)
(2.22)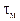 - коэффициент пропускания системы (по определению).
- коэффициент пропускания системы (по определению).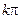 (k = 1,2,3...) и углах
(k = 1,2,3...) и углах 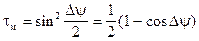 (2.23)
(2.23)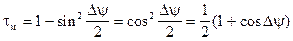 (2.24)
(2.24)


