Исследование электрооптических модуляторов на кристаллах симметрии 3m
Один из перспективных материалов для использования в электрооптических модуляторах (ЭОМ) являются ниобат лития (LiNbO3) и танталат лития (LiTaO3). Этот кристалл в отсутствие поля является одноосным и имеет симметрию 3m. Уравнение индикатрисы Уравнение индикатрисы кристалла определяется группой симметрии и приложенным электрическим полем. Для группы симметрии 3m отличными от нуля в матрице электрооптических коэффициентов будут следующие:
r12 = -r22; r13; r22; r23 = r13; r33; r42 = r51; r51; r61 = -2r22.
Тогда из (1.4), (2.4) получим индикатрису кристалла при приложении внешнего поля (Еx, Ey, Ez);
Из (2.29) видно, что два сильно отличающихся друг от друга случая будут получаться при приложении поля вдль оси x или y и вдоль оси z. а) поле приложено вдоль оси y (как в образце лабораторной установки) Е = (0,Е,0). В этом случае уравнение индикатрисы примет вид:
откуда видно, что изменятся показатели преломления по осям x и y, а эллипсоид индикатрисы повернется на угол
Новые показатели преломления будут равны соответственно:
Для данного случая, при распространении света вдоль оси z кристалла LiNbO3 разность показателей преломления
Схемы ориентации осей, иллюстрирующие этот случай показаны на рис. а- в отсутствии поля, на рис. б - при приложенном поле (0,Е,0). См. рис.2.11.
б) при приложении поля вдоль оси z и прохождении света вдоль оси y (см. рис.2.12) форма и положение оптической индикатрисы будет отличаться от первого варианта. Действительно, если подставим в уравнение (2.30) электрическое поле Еz = (0,0,Е) то получим:
Из (2.33) видно, что для осуществления изменения разности фаз компонент проходящего излучения необходимо, чтобы свет проходил вдоль оси x или y. В этом случае разность показателей преломления составит:
Таким образом получаем, что в отсутствии поля для света, проходящего через образец вдоль оси z существует некоторый фазовый сдвиг Далее из (2.33) можно видеть, что индикатриса не изменяет ориентации, но деформируется по всем трем осям при приложении поля:
Итак, в первом случае разность показателей преломления
Построение СМХ Одной из важных характеристик ЭОМ является полуволновое напряжение ( Для двух рассмотренных выше случаев Сравнив эти две величины, можно выбрать для каждого случая свою область применения.
2.5.Исследование квадратичного электрооптического эффекта в ЦТСЛ Помимо рассмотренных выше материалов существует множество сред, где проявляется квадратичный электрооптический эффект (эффект Керра). Примером такой среды является прозрачная оптическая керамика титаната цирконата свинца легированного лантаном (ЦТСЛ). Поскольку керамика это не кристаллическое вещество, то и ведет она себя в отсутствии поля как изотропная среда, т.е. показатели преломления равны по всем направлениям. При приложении поля индикатриса деформируется в направлении поля (эффект Керра). Эффект Керра состоит в том, что любая жидкость, газ (или твердое тело) при помещении их в равномерное электрическое поле (которое можно получить, например, между обкладками плоского конденсатора) становятся анизотропными. Ось анизотропии направлена в данном случае по направлению поля (перпендикулярно обкладкам конденсатора). Если свет проходит в направлении, перпендикулярном оси анизотропии (см. рис. 2.13), то образующаяся при этом разность хода
и
Коэффициент пропорциональности
Из всех жидких веществ, применяемых в практике модуляции света, наибольшим значением Если перейти от напряженности поля E (ед. CGSE) к напряжению на обкладках конденсатора (вольты), то формула (2.37) перепишется в виде:
Из выражения (2.38) можно найти величины напряжений, при которых модулятор изменяет свое пропускание на единицу. Положив
Минимальное значение uM, соответствующее k = 1, называется критическим или полуволновым напряжением модулятора. Оно обозначается через uk (или
Тогда формулу (2.38) с учетом (2.40) можно переписать в виде:
Размерность величины, входящих в (2.38): (2.41):
Формулы (2.42) и (2.43) устанавливают связь между напряжением на электроно-оптическом модуляторе Керра и интенсивностью потока оптического излучения на выходе модулятора (так как Схема эксперимента ля ЦТСЛ керамики (приложения напряжения и прохождения света) показана на рис.2.14.
При прохождении света перпендикулярно направлению приложенного поля (рис.2.14) между компонентами, распространяющимися вдоль осей х и z возникает фазовый сдвиг Согласно эффекту Керра в этом случае фазовый сдвиг будет пропорционален квадрату приложенного поля. Итак, в отсутствии поля
Построив СМХ для образца ЦТСЛ керамики можно убедиться в том, что зависимость фазового сдвига от приложенного поля квадратичная (2.44).
|


 (2.29)
(2.29) , (2.30)
, (2.30) в плоскости yz (вокруг оси x):
в плоскости yz (вокруг оси x):
 (2.31)
(2.31)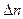 :
: (2.32)
(2.32)






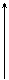






 Z Z
Z Z 
 (2.33)
(2.33)
 (2.34)
(2.34) ;
; 
 (2.35)
(2.35) .
. , во втором случае получим
, во втором случае получим  , где
, где  , т.е теперь
, т.е теперь  пропорциональна другим электрооптическим коэффициентам. Это говорит о том, что для достижения той же разности показателей преломления требуется другая величина приложенного к образцу напряжения.
пропорциональна другим электрооптическим коэффициентам. Это говорит о том, что для достижения той же разности показателей преломления требуется другая величина приложенного к образцу напряжения. ) - это напряжение, которое нужно приложить к нему, чтобы изменить пропускание на 1 (при
) - это напряжение, которое нужно приложить к нему, чтобы изменить пропускание на 1 (при  =
=  и положив k=1 - см. (2.24)).
и положив k=1 - см. (2.24)). . Для пояснения этого факта необходимо провести эксперимент с образцами 3m кристалла на лабораторной установке. Цель опыта заключается в том, чтобы определить полуволновые напряжения двух образцов. При этом нет необходимости строить СМХ полностью, а достаточно отследить лишь максимум пропускания с помощью фотоприемника - это и будет полуволновое напряжение.
. Для пояснения этого факта необходимо провести эксперимент с образцами 3m кристалла на лабораторной установке. Цель опыта заключается в том, чтобы определить полуволновые напряжения двух образцов. При этом нет необходимости строить СМХ полностью, а достаточно отследить лишь максимум пропускания с помощью фотоприемника - это и будет полуволновое напряжение. (и
(и  связаны с напряженностью управляющего поля E зависимостями:
связаны с напряженностью управляющего поля E зависимостями: (2.36)
(2.36) (2.37)
(2.37) (2.36) зависит от электрооптических свойств среды. Величину
(2.36) зависит от электрооптических свойств среды. Величину  , входящую в выражение (2.37), в литературе часто называют константой Керра. Из (2.37) видно, что, чем больше значение
, входящую в выражение (2.37), в литературе часто называют константой Керра. Из (2.37) видно, что, чем больше значение  характеризует данное вещество, тем меньшая величина напряженности электрического поля E требуется для осуществления модуляции.
характеризует данное вещество, тем меньшая величина напряженности электрического поля E требуется для осуществления модуляции.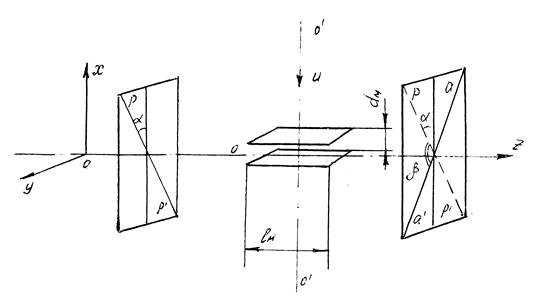
 (2.38)
(2.38) (k = 1, 2, 3 …), получим:
(k = 1, 2, 3 …), получим: (2.39)
(2.39) ) и равно
) и равно (2.40)
(2.40) (2.41)
(2.41) = 450;
= 450;  = 900
= 900 (2.42)
(2.42) (2.43)
(2.43) ). Это и есть статическая модуляционная характеристика для образца ЦТСЛ керамики.
). Это и есть статическая модуляционная характеристика для образца ЦТСЛ керамики.












 Z
I
Z
I

 , где
, где  .
. ,
,  ; при приложении поля:
; при приложении поля: и
и  . (2.44)
. (2.44)


