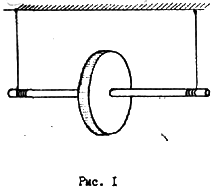
Краткая теория. Маятник Максвелла представляет собой массивный диск, ось которого подвешена на двух накрученных на нее нитях (рис
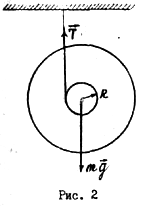
Если маятник отпустить, то он будет совершать возвратно-поступательное движение в вертикальной плоскости при одновременном вращении диска" вокруг оси. Силы, действующие на маятник, указаны на рис. 2.
Для описания движения маятника Максвелла удобно выбрать систему отсчета, связанную с центром масс маятника и имеющую одну ось, направленную вниз. Центром масс системы называют воображаемую точку, радиус-вектор которой определяется выражением
где т - масса системы,
то есть представляет собой произведение массы системы на скорость ее центра масс, что совершенно аналогично импульсу материальной точки. Таким образом, за движением центра масс можно следить, как за движением материальной точки. Исходя из этого, движение центра масс маятника Максвелла можно описать уравнением:
где m - масса маятника, Вращательное движение маятника описывается основным уравнением динамики вращательного движения, имеющий вид:
где ℐ - момент инерции, Моментом инерции тела относительно некоторой оси вращения называют величину
где
где r - расстояние от элементарной массы dm.
до оси вращения. Интегрирование должно производиться по всей массе тела. Маятник Максвелла можно представить в виде совокупности полых цилиндров и сплошного цилиндра - оси маятника. Рассчитаем, моменты инерции таких тел. Любое из этих тел можно мысленно разбить на тонкие цилиндрические слои, частицы которых находятся на одинаковом расстоянии от оси. Разобьем цилиндр радиуса R на концентрические слои толщиной dr. Пусть радиус какого - то слоя r, тогда масса частиц, заключенных в этом слое, равна
где dV - объем слоя, h - высота цилиндра,
Момент инерции всего цилиндра найдется интегрированием по всем слоям:
Так как масса цилиндра
Момент инерции полого цилиндра, имеющего внутренний радиус
Замечая, что масса полого цилиндра
Однако, аналитическое вычисление интегралов (5) возможно только в простейших случаях тел правильной геометрической формы. Для тел неправильной формы такие интегралы находят численно, либо используют косвенные методы определения момента инерции. Для нахождения момента инерции маятника Максвелла относительно его оси вращения можно воспользоваться уравнениями движения, (2), (3). Для решения дифференциальных уравнений (2) и (3) перейдем от векторной формы к скалярной. Спроектируем уравнение (2) на ось» совпадающую с направлением движения центра масс маятника. Тогда оно примет вид:
Рассмотрим проекции векторов
Составляющая момента силы относительно точки вдоль оси, проходящей через эту точку, называется моментом силы относительно оси. Вектор
где так как направление вектора ^ при опускании маятника со временем не меняется. Таким образом, уравнение (З) спроектируется, на ось вращения следующим образом: где
Дифференцируя это соотношение дважды, получим
Совместное решение уравнений (9) - (11) дает следующие выражения для линейного ускорения центра масс системы и результирующей силы натяжения:
Из (12), (13) видно, что ускорение диска и сила натяжения нити постоянны и ускорение всегда направлено вниз. Следовательно, если при опускании маятника координату его центра масс отсчитывать от точки его закрепления, то со временем координата будет меняться по закону
Подставляя (14) в (12), подучим для момента инерции маятника Максвелла следующее выражение
В неговходят величины, которые легко экспериментально измерить:
определяется по формуле
где D - диаметр оси маятника,
|

 (1) (I)
(1) (I)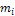 - массы материальных точек, составляющих эту систему,
- массы материальных точек, составляющих эту систему,  - их радиусы векторы. Величина
- их радиусы векторы. Величина 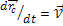 скорость движения этой воображаемой точки. Импульс системы с учетом (I) записывается в виде
скорость движения этой воображаемой точки. Импульс системы с учетом (I) записывается в виде ,
, (2)
(2) - линейное ускорение центра масс,
- линейное ускорение центра масс,  - результирующая сила натяжения обеих нитей.
- результирующая сила натяжения обеих нитей. (3)
(3) - результирующий момент сил, действующих на маятник относительно некоторой точки, лежащей да оси вращения,
- результирующий момент сил, действующих на маятник относительно некоторой точки, лежащей да оси вращения, 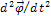 - угловое ускорение. Под вектором угла
- угловое ускорение. Под вектором угла  понимают вектор, по модули равный углу поворота
понимают вектор, по модули равный углу поворота  и направленный вдоль оси вращения так, чтобы с его начала поворот наблюдался происходящим по часовой стрелке.
и направленный вдоль оси вращения так, чтобы с его начала поворот наблюдался происходящим по часовой стрелке. , (4)(4)
, (4)(4)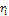 - расстояние от этих точек до оси вращения. Следовательно, момент инерции характеризует распределение массы тела относительно оси вращения. Из (4) видно, что момент инерции - величина аддитивная, то есть момент инерции тела равен сумме моментов инерции его частей. Если вещество в ней распределено непрерывно, то вычисление момента инерции сводится к вычислению интеграла
- расстояние от этих точек до оси вращения. Следовательно, момент инерции характеризует распределение массы тела относительно оси вращения. Из (4) видно, что момент инерции - величина аддитивная, то есть момент инерции тела равен сумме моментов инерции его частей. Если вещество в ней распределено непрерывно, то вычисление момента инерции сводится к вычислению интеграла ; (5)(5)
; (5)(5)
 ,
, - плотность вещества цилиндра. Все частицы слоя находятся на расстоянии r от оси, следовательно, момент инерции этого слоя
- плотность вещества цилиндра. Все частицы слоя находятся на расстоянии r от оси, следовательно, момент инерции этого слоя
 (6)
(6)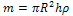 , то момент инерции сплошного цилиндра будет равен
, то момент инерции сплошного цилиндра будет равен (7)
(7) , а внешний
, а внешний  можно вычислить также по формуле (6), изменив в интеграле пределы интегрирования
можно вычислить также по формуле (6), изменив в интеграле пределы интегрирования
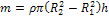 ,запишем момент инерции полого цилиндра следующим образом:
,запишем момент инерции полого цилиндра следующим образом: (8) - ( 8)
(8) - ( 8) (9)
(9)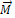 на ось координат, совпадающую с осью вращения и направленную по
на ось координат, совпадающую с осью вращения и направленную по  ,
,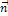 - единичный вектор, направленный вдоль
- единичный вектор, направленный вдоль  , а 5. Тогда угловое ускорение
, а 5. Тогда угловое ускорение (10) (10)
(10) (10) - радиус оси диска, на которую намотана нить,
- радиус оси диска, на которую намотана нить,  - угловое ускорение диска. Так как центр масс опускается на столь ко, на сколько раскручивается нить, то его перемещение x связано с углом, поворота
- угловое ускорение диска. Так как центр масс опускается на столь ко, на сколько раскручивается нить, то его перемещение x связано с углом, поворота 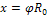
 (11)
(11) , (12)
, (12) (13)
(13) (14)
(14) ,где
,где  (15)
(15)  - внешний диаметр оси маятника вместе с намотанной на него нитью подвески, t - время опускания маятника, x - расстояние, пройденное центром масс маятника, m. - масса маятника, которая складывается из массы оси маятника, массы диска и массы кольца, надетого на диск. Внешний диаметр оси маятника вместе с намотанной на него нитью подвески
- внешний диаметр оси маятника вместе с намотанной на него нитью подвески, t - время опускания маятника, x - расстояние, пройденное центром масс маятника, m. - масса маятника, которая складывается из массы оси маятника, массы диска и массы кольца, надетого на диск. Внешний диаметр оси маятника вместе с намотанной на него нитью подвески (16)
(16) - диаметр нити.
- диаметр нити.


