Научный руководитель: к.ф.м.н. Прокопьев
При работе с прибором необходимо соблюдать правила безопасности, относящиеся к устройствам, в которых используется напряжение до 250 вольт. Эксплуатация прибора допускается только при наличии заземления.
Контрольные вопросы. 1. Сформулируйте теорему о движении центра масс системы материальных точек. 2. Дайте определение момента инерции одной материальной точки, системы материальных точек. 3. Запишите уравнения движения маятника Максвелла.
4. Как меняются ускорение, скорость и сила натяжения нитей при движении маятника? Как меняется механическая энергия маятника Максвелла при его движении?
Министерство образования Свердловской области МОУ Лицей 130 НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА ПО ФИЗИКЕ Тема «ОСОБЕННОСТИ СЛОЖНОГО ДВИЖЕНИЯ МАЯТНИКА МАКСВЕЛЛА» Исполнители: Ученики 10 класса Воротников Владислав Осинцев Степан Учитель: Научный руководитель: к.ф.м.н. Прокопьев Екатеринбург, 2011 г. Содержание.
Издревле людей привлекало внимание явление превращения поступательного механического движения во вращательное. Примеров тому немало. Но среди всех примеров один из наиболее ярких и интересных с научной точки зрения является пример маятника Максвелла. В отличие от обычного маятника, маятник Максвелла представляет собой массивный цилиндрический маховик (диск), насаженный на цилиндрическую ось и подвешенный за две тонкие и прочные нити (см. рисунок). Поворачивая маховик нить наматывают на ось, и, тем самым, поднимают маховик вверх. Затем маховик освобождают и маховик под действием силы тяжести начинает падать вниз, раскручивая при этом себя и ось. В нижнем положении происходит кратковременный удар и смена направления движения. Маховик по инерции, вращаясь в замедляющемся темпе, начинает накручивать нить и подниматься вверх до полной остановки. Затем процесс вновь и вновь повторяется.
Принцип работы маятника Максвелла основан на основных законах физики – законе сохранения энергии, который утверждает, что полная механическая энергия замкнутой консервативной системы во время движения системы не изменяется. (Замкнутая – значит, нет внешних сил, совершающих работу и увеличивающих или уменьшающих механическую энергию системы; консервативная – нет диссипативных (трения, сопротивления и т.д.) сил, превращающих механическую энергию системы во внутреннюю (тепло) и законе сохранения импульса) и законе сохранения импульса: полный импульс замкнутой системы – величина сохраняющаяся. Что же касается третьего закона механики – закона сохранения момента импульса системы, то его обычно в данной задаче не рассматривали, но здесь мы постараемся также детально обсудить.
Движение всякой частицы маховика можно представить как поступательное движение со скоростью оси с угловой скоростью Подсчитаем кинетическую энергию тела, совершающего плоское движение. Если рассматривать движение тела как чистое вращение вокруг мгновенной оси, то элемент массы Dmi имеет в данный момент линейную скорость v i = w ri, где ri – расстояние от этого элемента до мгновенной оси. Кинетическая энергия отдельного элемента тела будет: DEk,i = Dmi v i2/2 = Dmiw2ri2/2 а кинетическая энергия вращения всего тела
где
Введя в это выражение линейную скорость центра масс v = wr, получим
Полная кинетическая энергия плоского движения твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения вокруг оси, проходящей через центр масс тела. По закону сохранения энергии в механике полная энергия Е изолированной системы, в которой действуют только упругие силы и силы всемирного тяготения, есть величина постоянная: E = Ek + U = const где U – потенциальная энергия. В работе в начальный момент времени маятник находится в верхнем положении и обладает потенциальной энергией U и нулевой кинетической энергией: E k = 0. Когда маятник опустится и пройдет путь h, то потенциальная энергия U 1 = mgh перейдет в кинетическую энергию E поступательного и вращательного движения E k2: U 1 = E k2 или v
Так как w = v /r, где r – радиус оси, на которую намотаны нити, то уравнение (2) принимает вид:
Отсюда:
Движение маятника равноускоренное, следовательно, можно применить следующие формулы для пути и скорости:
v = v o + at В работе начальная скорость
v = at Из этой системы уравнений находим: v = 2 h/t Подставим полученное значение V в уравнение (3):
Эту же формулу можно получить другим
сти mg и натяжений нитей f. Ускорение а центра тяжести диска определяется уравнением: ma = mg – f (5) Ось моментов выберем так, чтобы она про- ходила через центр тяжести диска (т.е. совпадала с его геометрической осью О). Момент силы тяже- сти относительно этой оси равен нулю, а момент силы натяжения нитей M = f×r, и второй закон Ньютона для вращательного движения маятника имеет вид: Ioe = Iodw/dt = f×r (6) Из кинетических соображений легко найти связь между линейным ускорением а и угловым ускорением e = dw /dt. Так как центр тяжести опускается как раз на столько, на сколько раскручивается нить, то его перемещение h и угол поворота диска a связаны соотношением h = ar. Дифференцируя это соотношение дважды по времени, получим а = r×dw /dt, и уравнение (6) можно переписать в виде: (I o /r)a = f×r (7) Из уравнения (5) найдем:
Подставив (7) в (8), получим:
Ускорение а найдем из формулы пройденного пути маятника h: a = 2h/t2 и подставив в уравнение (7), получим
Это выражение аналогично формуле (4). Поскольку диаметр легче измерить, чем радиус, заменим r на 0,5d и получим окончательно такую формулу для Io:
Здесь Io – момент инерции маятника, m – масса маятника, d – диаметр валика, на который наматываются нити, g – ускорение свободного падения, h – расстояние, пройденное центром маятника за время t. Теперь уточним значение массы m и диаметра d. В данной работе маятник Максвелла представляет собой маховик с осью, на которые плотно насаживается съемное кольцо: m = mo + mм (10) mo – масса оси маятника, mм – масса собственно маховика, d = do + 2dп (11) где do – внешний диаметр оси маятника, dн – диаметр нити подвески.
|

 Введение
Введение , равной скорости центра масс, и вращение вокруг геометрической
, равной скорости центра масс, и вращение вокруг геометрической . Полную скорость любой точки получим, прибавив (векторно) к скорости
. Полную скорость любой точки получим, прибавив (векторно) к скорости 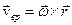 , обусловленной вращением, скорость поступательного движения
, обусловленной вращением, скорость поступательного движения  (1)
(1) – момент инерции тела относительно мгновенной оси. Но по теореме Гюйгенса - Штейнера I 1 = Io + mro2, где ro – расстояние от мгновенной оси до центра тяжести (в нашем случае – это радиус оси, на которую намотаны нити) и Io – момент инерции тела относительно оси, проходящей через центр тяжести. Поэтому из (1) получим:
– момент инерции тела относительно мгновенной оси. Но по теореме Гюйгенса - Штейнера I 1 = Io + mro2, где ro – расстояние от мгновенной оси до центра тяжести (в нашем случае – это радиус оси, на которую намотаны нити) и Io – момент инерции тела относительно оси, проходящей через центр тяжести. Поэтому из (1) получим: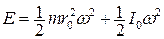 .
.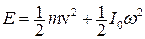 .
. (2)
(2)
 . (3)
. (3)
 h = v ot + at2/2
h = v ot + at2/2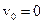 , тогда
, тогда
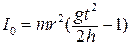 (4)
(4) способом. На диск массы m действуют сила тяже-
способом. На диск массы m действуют сила тяже- (8)
(8) .
.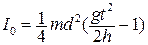 (9)
(9)


