Измерение момента инерции маятника
На ось маятника намотать нить подвески и зафиксировать ее. Проверить, отвечает ли нижняя грань кольца нулю шкалы на колонке. Если нет, отвинтить верхний кронштейн и отрегулировать его высоту. Привинтить верхний кронштейн. Нажать кнопку «ПУСК» миллисекундомера (сотового телефона). В момент прохождения маятником нижней точки остановить миллисекундомер. Намотать на ось маятника нить подвески, обращая внимание на то, чтобы она наматывалась равномерно, один виток рядом с другим. Фиксировать маятник, обращая внимание на то, чтобы нить в этом положении не была слишком скручена. Записать измеренное значение времени падения маятника. Определить замер времени n = 10 раз. Определить значение среднего времени падения маятника по формуле:
где n – количество выполненных замеров, ti – значение времени, полученное в i – том замере, t – среднее значение времени падения маятника. По шкале на вертикальной колонке прибора определить расстояние, проходимое маятником за время падения. Используя формулу (11) и известные значения диаметров dо и dн, определить диаметр оси вместе с намотанной на нее нитью. По формуле (10) вычислить массу маятника вместе с кольцом, наложенным в данном опыте. Значения масс отдельных элементов нанесены на них. По формуле (9) определить момент инерции маятника. Сравнить с теоретическим значением момента инерции Iтеор = Iо + Iм, где Iо – момент инерции оси, Iм - момент инерции маховика, которые вычисляются по следующим формулам: Iо = moro 2 / 2; Iк = mмrм 2 / 2.
Практические данные: Длина маятника. Таблица 1.
I1=(0.00090±0.00001) кг*м2.
Вывод: В ходе работы были определены моменты инерции маятника для разных длин намотанной нити и определены погрешности. Сравнение результатов расчётов и экспериментальное значение обнаруживает значительное различие данных.
Вывод: Мы определили экспериментальный и теоретический моменты инерции маятника, которые составили и сравнили их
1.1. Движение маятника Максвелла представляет собой пример плоского движения твердого тела, при котором траектории всех его точек лежат в параллельных плоскостях. Это движение может быть сведено к поступательному движению маятника и вращательному движению вокруг оси, проходящей через его центр масс перпендикулярно этим плоскостям. Такой тип движения широко распространен в технике: качение цилиндра по плоскости, колеса автомобиля, катка дорожной машины, движение вращающегося винта вертолета и т. д. 1.2. Целью настоящей лабораторной работы является экспериментальное ознакомление с плоским движением твердого тела на примере маятника Максвелла и определение момента инерции маятника. 2. ОСНОВНЫЕ ПОНЯТИЯ 2.1. Маховик совершает периодически повторяющееся движение, поэтому он получил название маятника. Итак, движение маятника Максвелла можно разделить на две стадии: опускание и подъем. 2.2. Согласно основным законам динамики поступательного и вращательного движения (для соответственных осей), пренебрегая силами трения о воздух и отклонением нитей от вертикали, запишем
где m - масса маятника, I - момент инерции маятника относительно оси,
Эти уравнения применимы как к первой, так и ко второй стадиям движения маятника. Начальные условия на разных стадиях различны: при опускании маятника начальная скорость его центра масс равна нулю, при его подъеме она отлична от нуля. 2.3.Из уравнений (1), (2), (3) следует
Из зависимости пути от времени при равноускоренном движении с нулевой начальной скоростью можно найти линейное ускорение маятника
где t - время движения маятника от верхней до нижней точки, h - расстояние, проходимое за это время. При
Отметим, что направления линейного ускорения и сил натяжения не зависят от того, куда движется маятник - вверх или вниз. За одно полное колебание линейная скорость меняет своё направление в нижней точке на противоположное, а линейное ускорение и силы не меняют. Угловая же скорость, наоборот, не меняет своего направления, а момент сил и угловое ускорение в нижней точке меняют на противоположные. 2.4.При подъеме вверх маятник движется равнозамедленно. Высота h2, на которую он поднимется, будет меньше, чем та, с которой опускается h1. Разность этих высот определяет убыль механической энергии, затраченной на преодоление сил деформации нитей при ударе и сил сопротивления движению. Доля потерянной механической энергии
ОПИСАНИЕ УСТАНОВКИ
3.1. Схема установки изображена на рис. 2. В основании 1 закреплена колонка 2, на ней держится верхний кронштейн 3, на котором находится электромагнит 4, фотоэлектрический датчик 5 и вороток 6 для выравнивания подвески маятника. К нижнему кронштейну прикреплен второй фотоэлектрический датчик 7. Маховик маятника Максвелла состоит из диска 8, насаженного на ось 9, и прикреплённого к нему массивного кольца 10. Он подвешен на двух параллельных нитях, намотанных на ось. Маятник удерживается в верхнем положении электромагнитом. Высоты опускания и подъёма маятника определяются по миллиметровой линейке 11, находящейся на колонке прибора. Миллисекундомер МС 12 предназначен для измерения времени t движения маятника Максвелла. Начало и окончание отсчёта времени осуществляются автоматически с помощью фотодатчиков, упомянутых выше. Определение момента инерции маятника Максвелла производится косвенным образом. Из уравнений (6) и (8) следует, что момент инерции можно рассчитать по формуле
Здесь m – полная масса маятника, m = m о + m д + m K, (11) где m о - масса оси, m д - масса диска,.
4. ПОРЯДОК ИЗМЕРЕНИЙ 4.1. Технические данные. 4.1.1. Внести данные установки в табл. 1. Таблица 1
4.1.2. Занести в табл. 2 значения масс и диаметров элементов маятника. Эти данные указаны на установке.
Таблица 2
4.2. 4.3. Определение момента инерции маятника Максвелла. 4.2.2. На ось маятника симметрично, виток к витку, намотать нити подвески и зафиксировать маятник. Работать следует очень аккуратно. 4.2.3. Отпустить маятник и запустить отсчёт времени. В нижней точке отсчёт остановить. 4.2.5. Измеренное значение времени движения маятника занести в табл.3. Повторяя операции по пунктам 4.2.2 и 4.2.3, провести измерение времени еще 10 раз и данные занести в табл. 3.
Таблица 3
4.3. Определение убыли механической энергии 4.3.1. По линейке определить высоту h 1, с которой опускается маятник; занести в табл. 3. 4.3.2. Повторить операции, описанные в п. 4.2.2 и 4.2.3, дать маятнику совершить пять полных колебаний, измерить разность высот d h. Это измерение произвести 1 раз и занести его результат в табл. 3.
5. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ 5.1. Определение момента инерции маятника Максвелла. Вычислить среднее значение времени движения маятника Вычислить среднюю квадратичную ошибку в измерении времени движения маятника
5.1.3. Вычислить абсолютную случайную ошибку D tсл = 2,1 DS. (13) 5.1.4. Вычислить полную абсолютную ошибку D t = D tсл + D tприб. (14) 5.1.5. Вычислить относительную ошибку
все вычисленные величины поместить в табл. 3. 5.1.6. По формуле (10) вычислить момент инерции маятника, подставляя в качестве 5.1.7. Вычислить относительную ошибку момента инерции маятника
где D m, D r о, D h1 - приборные погрешности соответственных величин, Dt – полная абсолютнаяпогрешность времени движения; m - суммарная масса маятника, вычисленная по формуле (11). 5.1.8. По полученному значению eJ рассчитать величину абсолютной ошибки DJ в определении момента инерции DJ = eJ·J =. (17) Округлить DJ до одной значащей цифры, а значения `J до разряда абсолютной ошибки. 5.1.9. Окончательный результат записать в виде J =`J ± D J = (±) кг × м 2. (18) 5.2. Определение убыли механической энергии при движении маятника Максвелла. 5.2.1. Формула (9) выражает долю механической энергии, потерянной за пять колебаний маятника Максвелла; за одно колебание доля будет в пять раз меньше:
6. ВОПРОСЫ, выносимые на ЗАЩИТУ РАБОТЫ 1. Основной закон динамики поступательного движения. 2. По данным табл. 2 рассчитать значения моментов инерции оси, диска и кольца. Сравнить их сумму с экспериментальным значением J. 3. Как изменяются импульс и осевой момент импульса маятника Максвелла в нижней точке его движения? Объясните причины. 4. Закон сохранения полной энергии для маятника Максвелла. 5. Найти линейную и угловую скорости маятника в нижней точке. 6. Момент инерции твердого тела (определение). От чего зависит его величина? 7. Найти отношение кинетической энергии поступательного движения к кинетической энергии вращательного движения для данного маятника Максвелла. 8. Как меняются линейное и угловое ускорения за период движения маятника Максвелла? 9. Импульс и осевой момент импульса твердого тела. 10. Оценить натяжение нитей при прохождении маятником нижней точки (продолжительность “удара” в ней принять равной Dt»0,05c). 11. Как изменится время движения маятника, если радиус его оси увеличить в два раза? 12. Кинетическая энергия поступательного и вращательного движения твердого тела. 13. Расчет момента инерции диска радиусом R, массой m относительно оси, проходящей через центр перпендикулярно его плоскости. 14. Какие силы и моменты сил действуют на маятник Максвелла при его движении? Как они изменяются за период? 15. Расчет момента инерции кольца радиусом R, массой m относительно оси, проходящей через центр перпендикулярно его плоскости. 16. Получить формулу (10), исходя из закона сохранения механической энергии. (Учесть, что для маятника Максвелла Еквр >> Екпост). 17. На каком участке движения маятника, верхнем или нижнем, потери механической энергии больше? Объяснить причины.
ЛИТЕРАТУРА.
|

 (12)
(12)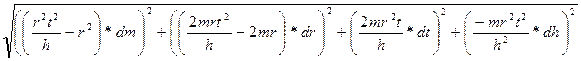 Подставив все и вычислив получим:
Подставив все и вычислив получим: Маятник Максвелла представляет собой небольшой маховик. Он может опускаться под действием силы тяжести и силы натяжения нитей, предварительно намотанных на ось маятника (рис.1). Нити во время движения вниз разматываются полностью. Раскрутившийся маховик продолжает вращаться в том же направлении и наматывает нити на ось, вследствие чего поднимается вверх, замедляя при этом свое движение. Дойдя до верхней точки -опять начинает опускаться вниз.
Маятник Максвелла представляет собой небольшой маховик. Он может опускаться под действием силы тяжести и силы натяжения нитей, предварительно намотанных на ось маятника (рис.1). Нити во время движения вниз разматываются полностью. Раскрутившийся маховик продолжает вращаться в том же направлении и наматывает нити на ось, вследствие чего поднимается вверх, замедляя при этом свое движение. Дойдя до верхней точки -опять начинает опускаться вниз. (1)
(1) (2)
(2) - радиус оси маятника, N - сила натяжения каждой нити, g - ускорение свободного падения, a - линейное ускорение центра масс маятника,
- радиус оси маятника, N - сила натяжения каждой нити, g - ускорение свободного падения, a - линейное ускорение центра масс маятника, 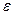 - угловое ускорение. Вследствие нерастяжимости нитей
- угловое ускорение. Вследствие нерастяжимости нитей . (3)
. (3) (4)
(4)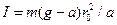 (5)
(5) , (6)
, (6) имеем
имеем 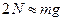 ; (7)
; (7)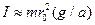 . (8)
. (8)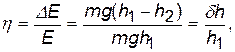 (9)
(9)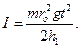 (10)
(10)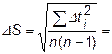
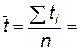
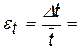

 и занести в табл. 3.
и занести в табл. 3. (12)
(12) , (15)
, (15) его среднее значение.
его среднее значение.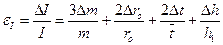 , (16)
, (16) . (19)
. (19)


