МЕТОДИКА ЭКСПЕРИМЕНТА
В ходе эксперимента проверяется основной закон динамики вращательного движения путем сравнения расчетного и экспериментально полученного значений момента инерции маятника Обербека. Расчетное значение момента инерции маятника получают как сумму моментов инерции всех его деталей:
где
Пренебрегая размерами груза по сравнению с радиусом вращения и используя формулу (6), найдем момент инерции груза относительно оси вращения:
где
Из рис. 1 видно, что расстояние от центра груза до оси вращения
где
Момент инерции стержня
где Подставляя выражения (13) и (15) в уравнение (12), получим, что расчетное значение момента инерции маятника Обербека можно вычислить по формуле
Для получения экспериментального значения момента инерции маятника Обербека рассмотрим действие сил, вызывающих его вращение. На маятник действуют сила тяжести, сила реакции опор подшипников и сила натяжения нити. Кроме того, со стороны подшипников на вращающуюся ось действуют силы трения. Сила тяжести и сила реакции опор, проходя через ось вращения, вращающих моментов не создают. Сила натяжения нити F передается ободу барабана и создает вращающий момент М. Силы трения создают тормозящий момент Под действием постоянных вращающего и тормозящего моментов маятник Обербека будет вращаться равноускоренно с угловым ускорением a. Основной закон динамики его вращательного движения, согласно уравнению (11), запишется в виде
Вращающий момент связан с силой натяжения нити и радиусом барабана соотношением
Для нахождения силы натяжения нити решим задачу динамики поступательно движущейся гири. На нее действуют две силы: сила тяжести m g, направленная вертикально вниз, и сила натяжения нити F, направленная вертикально вверх (рис. 2б). В соответствии со вторым законом Ньютона имеем m g + F = m a. (19)
а б
Рис. 2
Проецируя уравнение (19) на ось Y, получим:
где Ускорение гири можно определить из формулы пути равноускоренного падения без начальной скорости:
Из уравнений (20) и (21) получим, что сила натяжения нити
а вращающий момент
Как известно, угловое ускорение a связано с линейным ускорение
и, используя уравнение (21), для него получим:
Таким образом, измерив высоту и время падения гири, можно по формулам (23) и (25) вычислить вращающий момент и угловое ускорение для каждой серии опытов. Используя разные гири и барабаны, можно изменять вращающий момент. Момент инерции маятника – величина постоянная. Тормозящий момент от условий эксперимента зависит слабо, и его, в первом приближении, также можно считать постоянным. Это обстоятельство позволяет установить функциональную зависимость вращающего момента
Константы, входящие в формулу (26), определим, воспользовавшись методом наименьших квадратов и экспериментальными данными:
где
здесь a i и
Сравнивая уравнения (17) и (26), видим, что константа
Близость величины
|

 , (12)
, (12) – момент инерции груза;
– момент инерции груза; – момент инерции стержня.
– момент инерции стержня. , (13)
, (13) – масса груза;
– масса груза; – расстояние от центра груза до оси вращения.
– расстояние от центра груза до оси вращения. , (14)
, (14) – длина стержня;
– длина стержня; – длина груза.
– длина груза. , (15)
, (15) – масса стержня.
– масса стержня. . (16)
. (16) , препятствующий вращению маятника (рис. 2а).
, препятствующий вращению маятника (рис. 2а). . (17)
. (17) . (18)
. (18)
 , (20)
, (20) – ускорение свободного падения.
– ускорение свободного падения. , откуда
, откуда . (21)
. (21) , (22)
, (22) . (23)
. (23) простым соотношением
простым соотношением (24)
(24) . (25)
. (25) от углового ускорения маятника Обербека. Представим ее в виде линейной функции
от углового ускорения маятника Обербека. Представим ее в виде линейной функции . (26)
. (26) , (27)
, (27) , (28)
, (28) , (29)
, (29) – экспериментальные значения углового ускорения и вращающего момента, полученные в i -й серии опытов;
– экспериментальные значения углового ускорения и вращающего момента, полученные в i -й серии опытов; – число серий опытов (в табл. 2а
– число серий опытов (в табл. 2а  имеет смысл момента инерции, а константа
имеет смысл момента инерции, а константа  – смысл тормозящего момента. Поэтому можно положить, что
– смысл тормозящего момента. Поэтому можно положить, что , (30)
, (30)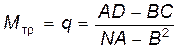 . (31)
. (31) к расчетному значению момента инерции
к расчетному значению момента инерции  подтверждает справедливость основного закона динамики вращательного движения. Что же касается величины тормозящего момента, то для обеспечения высокой точности результатов эксперимента должно выполняться неравенство
подтверждает справедливость основного закона динамики вращательного движения. Что же касается величины тормозящего момента, то для обеспечения высокой точности результатов эксперимента должно выполняться неравенство  . Соотношение этих двух величин позволяет, с одной стороны, ограничить снизу диапазон масс гирей, а, с другой стороны, оценить техническое состояние экспериментальной установки.
. Соотношение этих двух величин позволяет, с одной стороны, ограничить снизу диапазон масс гирей, а, с другой стороны, оценить техническое состояние экспериментальной установки.


