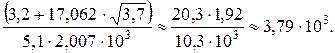Изучение теоретического материала.

 

1. Абрамов В.А. Сертификация продукции и услуг. Практическое пособие. М., 2001, 288с.

2. Богомолов Ю.А., Полковская Т.М., Филиппов М.Н. Основы метрологии. Ч.1.М., 2000. 111с.

3.Зайцев С.А., Толстов А.Н., Куранов А.Д. Нормирование точности. М.2004. 177с.

4.Зайцев С.А., Толстов А.Н., Куранов А.Д. Допуски, посадки и технические измерения в машиностроении. М.2004.102с.

5.Клевлев В.М., Попов Ю.П., Кузнецова И.А. Метрология. Стандартизация. Сертификация. М.2004.7с

 

Методические указания для студентов.

1.3.2.1. Общие положения.

Студенты выполняют в каждом семестре 2-3 блока-задания (модуля). Каждый модуль представляет некоторый раздел программы и состоит из самостоятельной контрольной работы (до 4 задач, в зависимости от специальности). Задачи модуля выполняются студентами в определенные сроки, указанные в программе; лабораторных работ, выполняемых и защищаемых на занятиях; и реферата, который представляется в конце семестра. Каждый из модулей студент защищает на индивидуальных занятиях, проводимых по расписанию. Защитой модуля считается успешная сдача коллоквиума.

Перед выполнением заданий модуля студентам предоставляется право ознакомления с рабочей программой по физике. На одном из первых занятий в семестре выдаются задания, варианты самостоятельной контрольной работы, график выполнения лабораторных занятий, темы рефератов. До их сведения доводятся сроки выполнения и защиты модулей и сдачи коллоквиумов, т.е. определяется изучения дисциплины.

Изучение теоретического материала.

Известно, что изучение любой дисциплины, в том числе и физики, необходимо начинать с изучения теоретических положений и законов, воспользовавшись учебником, учебным пособием, либо конспектом лекций. В рабочей программе представлены список литературы, с указанием параграфов или страниц соответствующего учебника, и методических пособий и указаний, которые необходимо использовать при выполнении задания модуля. Конспект лекций студенты обязаны вести на занятиях.

После изучения теории можно приступать к выполнению практических заданий, выполнению лабораторных работ и самостоятельной контрольной работы, так как знание законов физики предполагает умение не только формулировать эти законы, но и применять их в конкретных случаях при решении задач и проведении простейших физических экспериментов (опытов).

1.3.2.3. Практические занятия.

Цель практических занятий – путь усвоения теоретического материала, изучение количественных соотношений между физическими величинами и выработка навыков решения задач.

Занятия по решению задач (практические занятия) включают в себя:

а) теоретическую подготовку студентов к занятию, в ходе, которой, студент обязан осмыслить теоретический материал, выносимый на занятие, и заучить основные законы и формулы;

б) решение задач на самом практическом занятии;

в) выполнение домашнего задания (самостоятельное решение задач, которые предлагаются преподавателем к следующему практическому занятию).

Существуют различные приемы решения задач по физике, что обусловлено большим разнообразием самих задач.

Метод решения каждой задачи может быть различным и не только в зависимости от условий самой задачи, но и от индивидуальных особенностей студента.

Существуют три основных метода решения задач: алгебраический, геометрический и графический.

Используя наиболее распространенный алгебраический метод, составляют уравнения и системы уравнений на основе известных законов физики.

При решении задач геометрическим способом условие задачи представляется эскизом, а неизвестные физические величины определяются как геометрические элементы. Геометрический метод широко применяют в статике, геометрической оптике и в других разделах физики.

С геометрическим методом тесно связан графический метод, при использовании которого условие задачи представляется графиками физических величин, а конкретные их числовые значения вычисляются по графику (скорость тела, путь, сила тока, количество электричества, сила, энергия и т. п.).

В решении простых задач обычно достаточно использовать один из методов. Комплексные задачи требуют привлечения всех методов, но даже и в несложных задачах использованием комбинации методов облегчается обдумывание хода решения, четкое представление заданной ситуации.

Для выполнения расчетов используются два основных иногда противоположных способа – или последовательное вычисление всех промежуточных результатов, или алгебраический расчет (решение в общем виде) с подстановкой цифровых значений величин только в последнее выражение, определяющее искомую величину.

Решение задач с вычислением промежуточных результатов в наибольшей мере соответствует основной цели практических занятий – изучение количественных соотношений между физическими величинами. Вычисление промежуточных результатов дает достаточно полную количественную картину этих соотношений, более соответствует и основной цели практических занятий по физике и условиям приобретения знаний при изучении последующих величин, курсовом и дипломном проектировании и в последующей производственной деятельности.

Второй способ (решение в общем виде) обычно считается предпочтительным, так как приводит к искомому результату кратчайшим путем. Решение в общем виде дает цифровое значение только одной величины, а все остальные количественные связи, зачастую совершенно неявные, остаются скрытыми.

Особую роль в решении задач по физике играет получение числа, характеризующего физическую величину в конкретных условиях. Собственно определение чисел и выражает одну из основных целей физического практикума.

Немалую роль в физическом практикуме играет привитие навыков выполнения расчетов с разумной степенью точности, соответствующей заданной ситуации. В подавляющем большинстве вычислений целесообразно использование правил приближенных вычислений даже в том случае, когда вычисления производят с применением калькулятора или ЭВМ.

С определенной степенью точности правила приближенных вычислений можно свести к утверждению: в конечном ответе необходимо оставлять столько значащих цифр, сколько их в наименьшем числе, работающем в действии. Значащими называются все цифры кроме нуля, а также нуль в двух случаях: а) когда он стоит между значащими цифрами; б) когда он стоит в конце числа и когда известно, что единиц соответствующего разряда в данном числе не имеется.

Например,

1. При сложении и вычитании приближённых чисел окончательный результат округляют так, чтобы он не имел значащих цифр в тех разрядах, которые отсутствуют хотя бы в одном из слагаемых:

4,462 + 2,38 + 1,17273 + 1,0263 = 9,04093

Следует сумму округлить до сотых долей, т.е. принять её равной 9,04.

2. При умножении необходимо округлять сомножители так, чтобы каждый из них содержал столько значащих цифр, сколько их имеет сомножитель с наименьшим числом таких цифр.

Например, вместо вычисления выражения

3,723×2,4×5,1846

следует вычислять выражение

3,7×2,4×5,2.

В окончательном результате следует оставлять такое же число значащих цифр, какое имеется в сомножителях, после их округления.

В промежуточных результатах необходимо сохранять на одну значащую цифру больше. То же правило соблюдается и при делении приближённых чисел.

3. При возведении в квадрат или в другую степень следует в степени оставлять столько же значащих цифр, сколько их имеется в основании степени. Например,

1,32² ~ 1,74.

4. При извлечении корня любой степени в результате нужно брать столько значащих цифр, сколько их имеется в подкоренном выражении. Например,

(1,17×10^-8)^1/2 ~ 1,08×10^-4.

5.При вычислении сложных выражений следует применять указанные правила в соответствии с видом производимых действий. Например,

(3,2+17,062)× /5,1×2,007×10³

Сомножитель 5,1 имеет наименьшее число значащих цифр - две. Поэтому -результаты всех промежуточных вычислений должны округляться до трех значащих цифр:

После округления результата до двух значащих цифр получаем 3,8×10^-3.

Помимо решения задач на практических занятиях студентам предлагается домашнее задание в виде 5-7 задач, которые он обязан решить к следующему практическому занятию по расписанию с использованием изложенного выше.