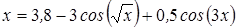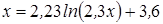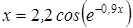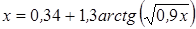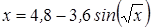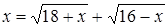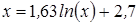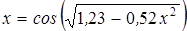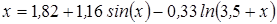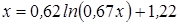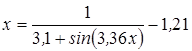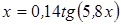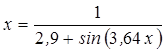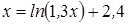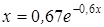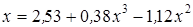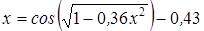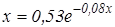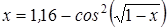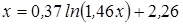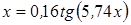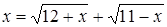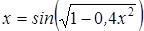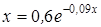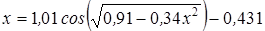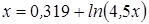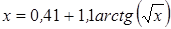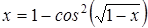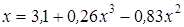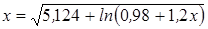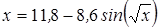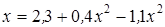Нахождение корня уравнения методом простых итераций
Цель:
- методом простых итераций вычислить корень уравнения вида x=f(x), расположенный на интервале [ a; b], с абсолютной погрешностью ε;(№ 3.1-3.120, таблица 3.1);
- определить число итераций, необходимое для нахождения корня;
- значение корня выводить через заданное в задании число итераций (по усмотрению преподавателя).
Таблица 3.1
| №
задачи
| Уравнение
| Интервал
[a; b]
| погрешность
ε
| Шаг вывода значения корня
| | 3.1
| 
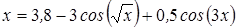
| [6; 8]
| 0,00015
| 1
| | 3.2
| 
| [5; 7]
| 0,000025
| 2
| | 3.3
| 
| [-1; 2]
| 0,000035
| 3
| | 3.4
| 
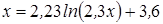
| [9; 12]
| 0,0000015
| 4
| | 3.5
| 
| [-1; 0]
| 0,000025
| 1
| | 3.6
| 
| [1; 3]
| 0,00015
| 2
| | 3.7
| 
| [1; 2]
| 0,00035
| 3
| | 3.8
| 
| [-1; 1]
| 0,00015
| 4
| | 3.9
| 
| [0; 2]
| 0,00055
| 1
| | 3.10
| 
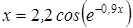
| [2; 5]
| 0,0005
| 2
| | 3.11
| 
| [0; 2]
| 0,00015
| 3
| | 3.12
| 
| [0; 2]
| 0,00000125
| 4
| | 3.13
| 
| [0; 3]
| 0,0000125
| 1
| | 3.14
| 
| [0; 1]
| 0,0000055
| 2
| | 3.15
| 
| [2; 5]
| 0.0000125
| 3
| | Продолжение табл. 3.1
| | №
задачи
| Уравнение
| Интервал
[a; b]
| погрешность
ε
| Шаг вывода значения корня
| | 3.16
| 
| [-1; 2]
| 0,000025
| 4
| | 3.17
| 
| [1; 4]
| 0,000225
| 1
| | 3.18
| 
| [-1; 2]
| 0,000125
| 2
| | 3.19
| 
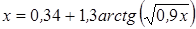
| [1; 2]
| 0,0000215
| 3
| | 3.20
| 
| [0,2; 1,2]
| 0,000225
| 4
| | 3.21
| 
| [-2; 0]
| 0,000125
| 1
| | 3.22
| 
| [3; 5]
| 0,000225
| 2
| | 3.23
| 
| [-2; 1]
| 0,000025
| 3
| | 3.24
| 
| [-2; 1]
| 0,000125
| 4
| | 3.25
| 
| [1; 3]
| 0,000125
| 1
| | 3.26
| 
| [4; 6]
| 0,000015
| 2
| | 3.27
| 
| [1; 4]
| 0,000135
| 3
| | 3.28
| 
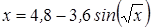
| [2; 4]
| 0,000025
| 4
| | 3.29
| 
| [0; 2]
| 0,000015
| 1
| |
| | Продолжение табл. 3.1
| | №
задачи
| Уравнение
| Интервал
[a; b]
| погрешность
ε
| Шаг вывода значения корня
| | 3.30
| 
| [0; 3]
| 0,000155
| 2
| | 3.31
| 
| [0; 2]
| 0,00015
| 3
| | 3.32
| 
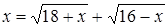
| [6; 8]
| 0,000025
| 4
| | 3.33
| 
| [1; 2]
| 0,000035
| 1
| | 3.34
| 
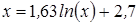
| [4; 6]
| 0,0000015
| 2
| | 3.35
| 
| [0; 1]
| 0,000025
| 3
| | 3.36
| 
| [0; 1]
| 0,00015
| 4
| | 3.37
| 
| [1; 2]
| 0,00035
| 1
| | 3.38
| 
| [0; 1]
| 0,00015
| 2
| | 3.39
| 
| [0; 2]
| 0,00055
| 3
| | 3.40
| 
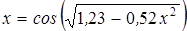
| [-1; 0]
| 0,0005
| 4
| | 3.41
| 
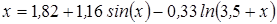
| [2; 3]
| 0,00015
| 1
| | 3.42
| 
| [1; 2]
| 0,00000125
| 2
| | 3.43
| 
| [0; 1]
| 0,0000125
| 3
| | |
|
|
|
| | Продолжение табл. 3.1
| | №
задачи
| Уравнение
| Интервал
[a; b]
| погрешность
ε
| Шаг вывода значения корня
| | 3.44
| 
| [-1; 0]
| 0,0000055
| 4
| | 3.45
| 
| [2; 3]
| 0,0000125
| 1
| | 3.46
| 
| [-1; 2]
| 0,000025
| 5
| | 3.47
| 
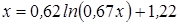
| [1; 2]
| 0,000225
| 1
| | 3.48
| 
| [-1; 3]
| 0,000125
| 2
| | 3.49
| 
| [1; 3]
| 0,0000215
| 3
| | 3.50
| 
| [0; 1]
| 0,000225
| 4
| | 3.51
| 
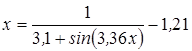
| [-1; 2]
| 0,000215
| 5
| | 3.52
| 
| [2; 4]
| 0,000225
| 1
| | 3.53
| 
| [1; 2]
| 0,000025
| 2
| | 3.54
| 
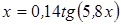
| [0; 1]
| 0,000125
| 3
| | 3.55
| 
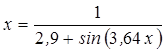
| [0; 1]
| 0,000125
| 4
| | 3.56
| 
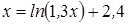
| [3; 5]
| 0,000015
| 5
| | 3.57
| 
| [1; 3]
| 0,000135
| 1
| | 3.58
| 
| [18; 22]
| 0,000025
| 2
| | Продолжение табл. 3.1
| | №
задачи
| Уравнение
| Интервал
[a; b]
| погрешность
ε
| Шаг вывода значения корня
| | 3.59
| 
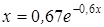
| [0; 1]
| 0,000015
| 3
| | 3.60
| 
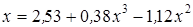
| [1; 3]
| 0,000155
| 4
| | 3.61
| 
| [1; 3]
| 0,00015
| 5
| | 3.62
| 
| [5; 7]
| 0,000025
| 2
| | 3.63
| 
| [0; 1]
| 0,000035
| 3
| | 3.64
| 
| [2; 4]
| 0,0000015
| 4
| | 3.65
| 
| [0; 1]
| 0,000025
| 5
| | 3.66
| 
| [0; 1]
| 0,00015
| 1
| | 3.67
| 
| [1; 2]
| 0,00035
| 2
| | 3.68
| 
| [0; 1]
| 0,00015
| 3
| | 3.69
| 
| [0; 2]
| 0,00055
| 4
| | 3.70
| 
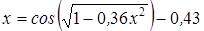
| [0; 1]
| 0,0005
| 5
| | 3.71
| 
| [-1; 1]
| 0,00015
| 1
| | 3.72
| 
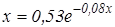
| [0; 1]
| 0,00000125
| 2
| | Продолжение табл. 3.1
| | №
задачи
| Уравнение
| Интервал
[a; b]
| погрешность
ε
| Шаг вывода значения корня
| | 3.73
| 
| [; 1]
| 0,0000125
| 3
| | 3.74
| 
| [0; 1,5]
| 0,0000055
| 4
| | 3.75
| 
| [2; 3]
| 0,0000125
| 5
| | 3.76
| 
| [-2; 1]
| 0,000025
| 1
| | 3.77
| 
| [2; 3]
| 0,000225
| 2
| | 3.78
| 
| [-1; 2]
| 0,000125
| 3
| | 3.79
| 
| [1; 2]
| 0,0000215
| 4
| | 3.80
| 
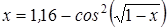
| [0; 1]
| 0,000225
| 5
| | 3.81
| 
| [-1; 2]
| 0,000125
| 1
| | 3.82
| 
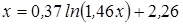
| [2; 3]
| 0,000225
| 2
| | 3.83
| 
| [1; 3]
| 0,000025
| 3
| | 3.84
| 
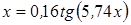
| [-1; 2]
| 0,000125
| 4
| | 3.85
| 
| [0; 1]
| 0,000125
| 5
| | 3.86
| 
| [3; 5]
| 0,000015
| 1
| | 3.87
| 
| [1; 3]
| 0,000135
| 2
| | Продолжение табл. 3.1
| | №
задачи
| Уравнение
| Интервал
[a; b]
| погрешность
ε
| Шаг вывода значения корня
| | 3.88
| 
| [18; 25]
| 0,000025
| 3
| | 3.89
| 
| [0; 1]
| 0,000015
| 4
| | 3.90
| 
| [1; 2,5]
| 0,000155
| 5
| | 3.91
| 
| [1; 3]
| 0,00015
| 1
| | 3.92
| 
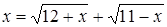
| [3; 7]
| 0,000025
| 2
| | 3.93
| 
| [0; 1]
| 0,000035
| 3
| | 3.94
| 
| [2; 4]
| 0,0000015
| 4
| | 3.95
| 
| [0; 1]
| 0,000025
| 5
| | 3.96
| 
| [0; 1]
| 0,00015
| 1
| | 3.97
| 
| [1,2; 2]
| 0,00035
| 2
| | 3.98
| 
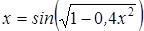
| [0; 1]
| 0,00015
| 3
| | 3.99
| 
| [0; 1,5]
| 0,00055
| 4
| | 3.100
| 
| [0; 1,1]
| 0,0005
| 5
| | 3.101
| 
| [-1; 1]
| 0,00015
| 1
| |
| | Продолжение табл. 3.1
| | №
задачи
| Уравнение
| Интервал
[a; b]
| погрешность
ε
| Шаг вывода значения корня
| | 3.102
| 
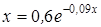
| [0; 2]
| 0,00000125
| 2
| | 3.103
| 
| [0; 1]
| 0,0000125
| 3
| | 3.104
| 
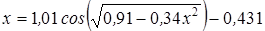
| [0; 1,6]
| 0,0000055
| 4
| | 3.105
| 
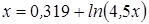
| [2; 3]
| 0,0000125
| 5
| | 3.106
| 
| [-1; 2]
| 0,000025
| 1
| | 3.107
| 
| [1; 2]
| 0,000225
| 2
| | 3.108
| 
| [-1; 0,5]
| 0,000125
| 3
| | 3.109
| 
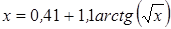
| [1; 2]
| 0,0000215
| 4
| | 3.110
| 
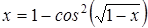
| [0; 1]
| 0,000225
| 5
| | 3.111
| 
| [-1; 0,85]
| 0,000125
| 1
| | 3.112
| 
| [2; 4]
| 0,000225
| 2
| | 3.113
| 
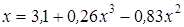
| [1; 3]
| 0,000025
| 3
| | 3.114
| 
| [-2; 1]
| 0,000125
| 4
| |
| | Продолжение табл. 3.1
| | №
задачи
| Уравнение
| Интервал
[a; b]
| погрешность
ε
| Шаг вывода значения корня
| | 3.115
| 
| [0; 0,85]
| 0,000125
| 5
| | 3.116
| 
| [2; 4]
| 0,000015
| 1
| | 3.117
| 
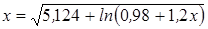
| [1; 3]
| 0,000135
| 2
| | 3.118
| 
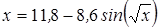
| [2; 5]
| 0,000025
| 3
| | 3.119
| 
| [0; 1]
| 0,000015
| 4
| | 3.120
| 
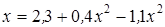
| [1; 2,5]
| 0,000155
| 5
|
Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
Подкожное введение сывороток по методу Безредки. С целью предупреждения развития анафилактического шока и других аллергических реакций при введении иммунных сывороток используют метод Безредки для определения реакции больного на введение сыворотки...
Принципы и методы управления в таможенных органах Под принципами управления понимаются идеи, правила, основные положения и нормы поведения, которыми руководствуются общие, частные и организационно-технологические принципы...
ПРОФЕССИОНАЛЬНОЕ САМОВОСПИТАНИЕ И САМООБРАЗОВАНИЕ ПЕДАГОГА Воспитывать сегодня подрастающее поколение на современном уровне требований общества нельзя без постоянного обновления и обогащения своего профессионального педагогического потенциала...
|
Понятие о синдроме нарушения бронхиальной проходимости и его клинические проявления Синдром нарушения бронхиальной проходимости (бронхообструктивный синдром) – это патологическое состояние...
Опухоли яичников в детском и подростковом возрасте Опухоли яичников занимают первое место в структуре опухолей половой системы у девочек и встречаются в возрасте 10 – 16 лет и в период полового созревания...
Способы тактических действий при проведении специальных операций Специальные операции проводятся с применением следующих основных тактических способов действий: охрана...
|
|
