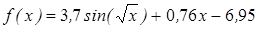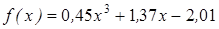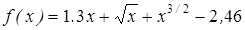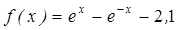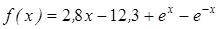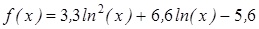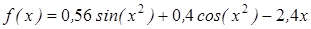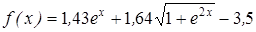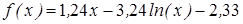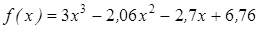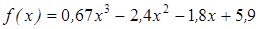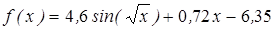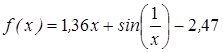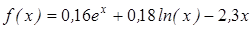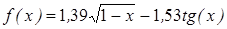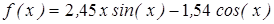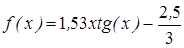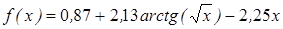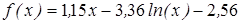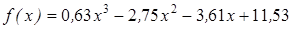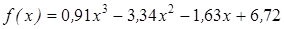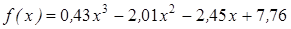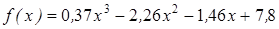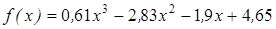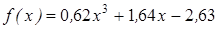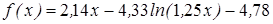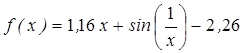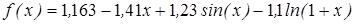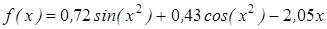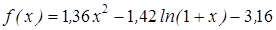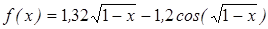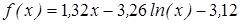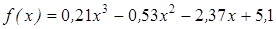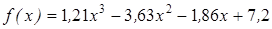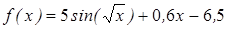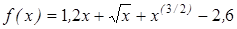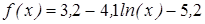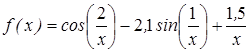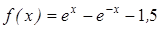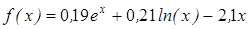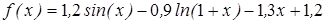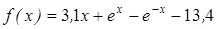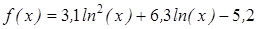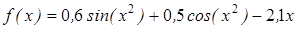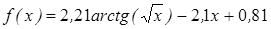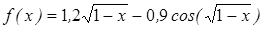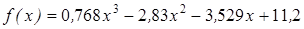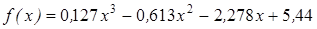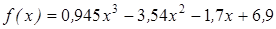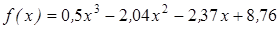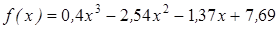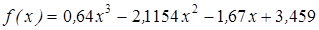Нахождение корня уравнения методом деления пополам.
Цель:
- методом деления пополам вычислить корень уравнения, расположенный на интервале [ a; b], с абсолютной погрешностью ε;(№3.121-3.240, таблица 3.2);
- определить число итераций, необходимое для нахождения корня.
Таблица 3.2
| №
задачи
| Уравнение
| Интервал
[a; b]
| Погрешность
ε
| | 3.121
| 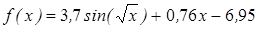
| [4; 7]
| 0,0005
| | Продолжение табл. 3.2
| | №
задачи
| Уравнение
| Интервал
[a; b]
| Погрешность
ε
| | 3.122
| 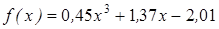
| [0; 2]
| 0,000015
| | 3.123
| 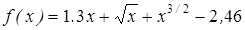
| [0,4; 1]
| 0,00005
| | 3.124
| 
| [9; 10]
| 0,000001
| | 3.125
| 
| [1; 2]
| 0,00005
| | 3.126
| 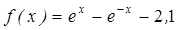
| [0; 1]
| 0,000125
| | 3.127
| 
| [1; 2]
| 0,00015
| | 3.128
| 
| [3; 4]
| 0,00035
| | 3.129
| 
| [0; 1,5]
| 0,00025
| | 3.130
| 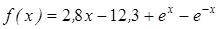
| [1; 3]
| 0,00015
| | 3.131
| 
| [0; 1]
| 0.0001
| | 3.132
| 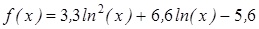
| [1; 3]
| 0,0000025
| | 3.133
| 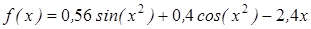
| [0; 1]
| 0,000015
| | 3.134
| 
| [2; 3]
| 0,000005
| | 3.135
| 
| [0,4; 1]
| 0,000015
| |
| | Продолжение табл. 3.2
| | №
задачи
| Уравнение
| Интервал
[a; b]
| Погрешность
ε
| | 3.136
| 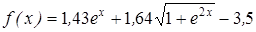
| [-1; 0]
| 0,00005
| | 3.137
| 
| [1; 2]
| 0,00025
| | 3.138
| 
| [0,2; 1]
| 0,00015
| | 3.139
| 
| [1; 2]
| 0,000025
| | 3.140
| 
| [0; 1]
| 0,000125
| | 3.141
| 
| [0; 0,85]
| 0,00015
| | 3.142
| 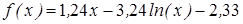
| [0,2; 0,7]
| 0,00025
| | 3.143
| 
| [1; 3]
| 0,00005
| | 3.144
| 
| [1; 2]
| 0,00025
| | 3.145
| 
| [0,7; 1,6]
| 0,0001
| | 3.146
| 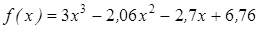
| [1; 2]
| 0,00005
| | 3.147
| 
| [1; 2]
| 0,00015
| | 3.148
| 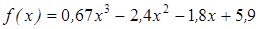
| [1; 3]
| 0,00001
| | 3.149
| 
| [1; 2]
| 0,00005
| |
| | Продолжение табл. 3.2
| | №
задачи
| Уравнение
| Интервал
[a; b]
| Погрешность
ε
| | 3.150
| 
| [1; 2,5]
| 0,0001
| | 3.151
| 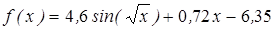
| [2; 3]
| 0,0005
| | 3.152
| 
| [0; 2]
| 0,000015
| | 3.153
| 
| [0,4; 1]
| 0,00005
| | 3.154
| 
| [8; 9]
| 0,000001
| | 3.155
| 
| [1; 2]
| 0,00005
| | 3.156
| 
| [0; 1]
| 0,000125
| | 3.157
| 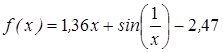
| [1; 2]
| 0,00015
| | 3.158
| 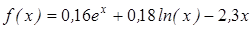
| [4; 5]
| 0,00035
| | 3.159
| 
| [0; 1,5]
| 0,00025
| | 3.160
| 
| [1; 3]
| 0,00015
| | 3.161
| 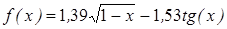
| [0; 1]
| 0,0001
| | 3.162
| 
| [1; 3]
| 0,0000025
| |
| | Продолжение табл. 3.2
| | №
задачи
| Уравнение
| Интервал
[a; b]
| Погрешность
ε
| | 3.163
| 
| [0; 1]
| 0,000015
| | 3.164
| 
| [2; 3]
| 0,000005
| | 3.165
| 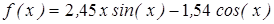
| [0,4; 1]
| 0,000015
| | 3.166
| 
| [-3; -1]
| 0,00005
| | 3.167
| 
| [1; 2]
| 0,00025
| | 3.168
| 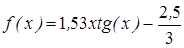
| [0,2; 1]
| 0,00015
| | 3.169
| 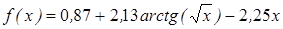
| [1; 2]
| 0,000025
| | 3.170
| 
| [0; 1]
| 0,000125
| | 3.171
| 
| [0; 0,85]
| 0,00015
| | 3.172
| 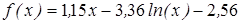
| [0,2; 0,7]
| 0,00025
| | 3.173
| 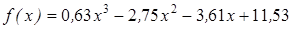
| [1; 3]
| 0,00005
| | 3.174
| 
| [1; 2]
| 0,00025
| | 3.175
| 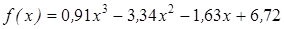
| [0,7; 1,6]
| 0,0001
| | 3.176
| 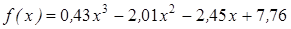
| [1; 2]
| 0,00005
| |
| | Продолжение табл. 3.2
| | №
задачи
| Уравнение
| Интервал
[a; b]
| Погрешность
ε
| | 3.177
| 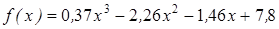
| [1; 2]
| 0,00015
| | 3.178
| 
| [1; 3]
| 0,00001
| | 3.179
| 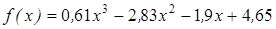
| [1; 2]
| 0,00005
| | 3.180
| 
| [1; 2,5]
| 0,0001
| | 3.181
| 
| [2; 3]
| 0,0005
| | 3.182
| 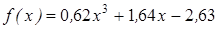
| [0; 2]
| 0,000015
| | 3.183
| 
| [0,4; 1]
| 0,00005
| | 3.184
| 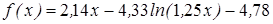
| [6; 7]
| 0,000001
| | 3.185
| 
| [1; 2]
| 0,00005
| | 3.186
| 
| [0; 1]
| 0,000125
| | 3.187
| 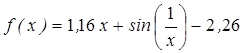
| [1; 2]
| 0,00015
| | 3.188
| 
| [4; 5]
| 0,00035
| | 3.189
| 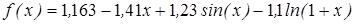
| [1; 2]
| 0,00025
| |
| | Продолжение табл. 3.2
| | №
задачи
| Уравнение
| Интервал
[a; b]
| Погрешность
ε
| | 3.190
| 
| [1; 3]
| 0,00015
| | 3.191
| 
| [0; 1]
| 0,0001
| | 3.192
| 
| [1; 3]
| 0,0000025
| | 3.193
| 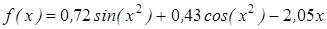
| [0; 1]
| 0,000015
| | 3.194
| 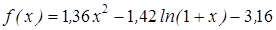
| [1; 2]
| 0,000005
| | 3.195
| 
| [0,4; 1]
| 0,000015
| | 3.196
| 
| [-2; 0]
| 0,00005
| | 3.197
| 
| [1; 2]
| 0,00025
| | 3.198
| 
| [0,2; 1]
| 0,00015
| | 3.199
| 
| [1; 2]
| 0,000025
| | 3.200
| 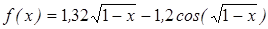
| [0; 1]
| 0,000125
| | 3.201
| 
| [0; 0,85]
| 0,00015
| | 3.202
| 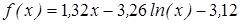
| [0,2; 0,7]
| 0,00025
| | 3.203
| 
| [1; 3]
| 0,00005
| | 3.204
| 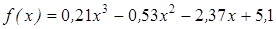
| [1; 2]
| 0,00025
| |
| | Продолжение табл. 3.2
| | №
задачи
| Уравнение
| Интервал
[a; b]
| Погрешность
ε
| | 3.205
| 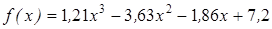
| [0,7; 1,6]
| 0,0001
| | 3.206
| 
| [1; 2]
| 0,00005
| | 3.207
| 
| [1; 2]
| 0,00015
| | 3.208
| 
| [1; 3]
| 0,00001
| | 3.211
| 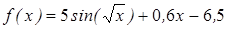
| [2; 3]
| 0,0005
| | 3.212
| 
| [0, 2]
| 0,000015
| | 3.213
| 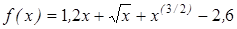
| [0,4; 1]
| 0,00005
| | 3.214
| 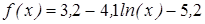
| [2; 4]
| 0,000001
| | 3.215
| 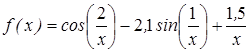
| [1; 2]
| 0,00005
| | 3.216
| 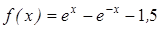
| [0; 1]
| 0,000125
| | 3.217
| 
| [1,2; 2]
| 0,00015
| | 3.218
| 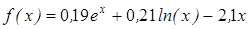
| [3; 4]
| 0,00035
| | 3.219
| 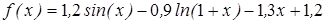
| [0; 1,5]
| 0,00025
| | 3.220
| 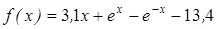
| [1; 3]
| 0,00015
| |
| |
| | Продолжение табл. 3.2
| | №
задачи
| Уравнение
| Интервал
[a; b]
| Погрешность
ε
| | 3.221
| 
| [0; 1]
| 0,0001
| | 3.222
| 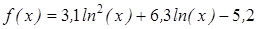
| [1; 3]
| 0,0000025
| | 3.223
| 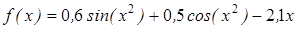
| [0; 1]
| 0,000015
| | 3.224
| 
| [2; 3]
| 0,000005
| | 3.225
| 
| [0,4; 1]
| 0,000015
| | 3.226
| 
| [-1; 0]
| 0,00005
| | 3.227
| 
| [2; 3]
| 0,00025
| | 3.228
| 
| [0,2; 1]
| 0,00015
| | 3.229
| 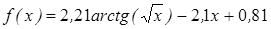
| [1; 2]
| 0,000025
| | 3.230
| 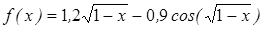
| [0; 1]
| 0,000125
| | 3.231
| 
| [0; 0,85]
| 0,00015
| | 3.232
| 
| [0,2; 0,7]
| 0,00025
| |
| | Продолжение табл. 3.2
| | №
задачи
| Уравнение
| Интервал
[a; b]
| Погрешность
ε
| | 3.233
| 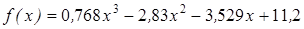
| [1; 3]
| 0,00005
| | 3.234
| 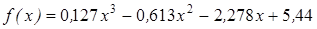
| [1; 2]
| 0,00025
| | 3.235
| 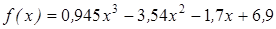
| [0,7; 1,6]
| 0,0001
| | 3.236
| 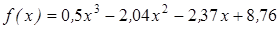
| [1,5; 2,4]
| 0,00005
| | 3.237
| 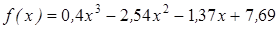
| [1; 2]
| 0,00015
| | 3.238
| 
| [1; 3]
| 0,00001
| | 3.239
| 
| [0,5; 1,4]
| 0,00005
| | 3.240
| 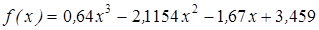
| [1; 2,5]
| 0,0001
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
Гидравлический расчёт трубопроводов Пример 3.4. Вентиляционная труба d=0,1м (100 мм) имеет длину l=100 м. Определить давление, которое должен развивать вентилятор,
если расход воздуха, подаваемый по трубе, . Давление на выходе . Местных сопротивлений по пути не имеется. Температура...
Огоньки» в основной период В основной период смены могут проводиться три вида «огоньков»: «огонек-анализ», тематический «огонек» и «конфликтный» огонек...
Упражнение Джеффа. Это список вопросов или утверждений, отвечая на которые участник может раскрыть свой внутренний мир перед другими участниками и узнать о других участниках больше...
|
Понятие и структура педагогической техники Педагогическая техника представляет собой важнейший инструмент педагогической технологии, поскольку обеспечивает учителю и воспитателю возможность добиться гармонии между содержанием профессиональной деятельности и ее внешним проявлением...
Репродуктивное здоровье, как составляющая часть здоровья человека и общества
Репродуктивное здоровье – это состояние полного физического, умственного и социального благополучия при отсутствии заболеваний репродуктивной системы на всех этапах жизни человека...
Случайной величины Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):
Понятие плотность распределения вероятностей случайной величины Х для дискретной величины неприменима...
|
|