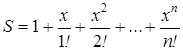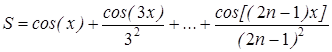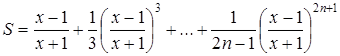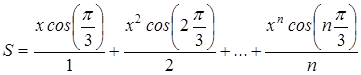Вычисление суммы членов бесконечного ряда
Цель:
- методом итераций вычислить сумму членов бесконечного ряда с заданной погрешностью ε;
- определить число рассчитанных членов ряда, необходимое для нахождения суммы.
Результатом работы является:
- разработанный алгоритм решения задачи в соответствии с вариантом задания (№ 3.241 – № 3.271, таблица 3.3), представленный в виде блок-схемы;
- программа решения задачи на соответствующем языке программирования, соответствующая варианту задания и блок-схеме;
- тестовый вариант исходных данных для проверки работоспособности алгоритма и программы;
- результаты работы программы по тестовому, разработанному студентом, варианту исходных данных.
Таблица.3.3
| | №
задачи
| Уравнение
| Интервал
аргумента
[a; b]
| погрешность
ε
| | | 3.241
| 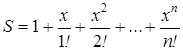
| [0; 2]
| 0,00001
| | | 3.242
| 
| [,1; 1]
| 0,0001
| | | 3.243
| 
| [1; 2]
| 0,0001
| | | 3.244
| 
| [0; 1]
| 0,00001
| | | 3.245
| 
| [π/5; 9π/5]
| 0,0001
| | | Продолжение табл. 3.3
| | | №
задачи
| Уравнение
| Интервал
аргумента
[a; b]
| погрешность
ε
| | | 3.246
| 
| [0; 1]
| 0,00005
| | | 3.247
| 
| [0,1; 0,8]
| 0,0001
| | | 3.248
| 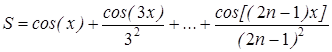
| [π/5; π]
| 0,0001
| | | 3.249
| 
| [0,1; 0,5]
| 0,0001
| | | 3.250
| 
| [0,1; 0,8]
| 0,0005
| | | 3.251
| 
| [0; 1]
| 0,0001
| | | 3.252
| 
| [0; 1]
| 0,0001
| | | 3.253
| 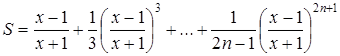
| [0,2; 1]
| 0,001
| | | 3.254
| 
| [π/5; π]
| 0,005
| | | 3.255
| 
| [0,1; 1]
| 0,0001
| | | 3.256
| 
| [0,1; 0,8]
| 0,0005
| | | Продолжение табл. 3.3
| | | №
задачи
| Уравнение
| Интервал
аргумента
[a; b]
| погрешность
ε
| | | 3.257
| 
| [0,1; 1]
| 0,0001
| | | 3.258
| 
| [0,1; 0,8]
| 0,0005
| | | 3.259
| 
| [1; 2]
| 0,0001
| | | 3.260
| 
| [1; 2]
| 0,0005
| | | 3.261
| 
| [0,1; 0,8]
| 0,00001
| | | 3.262
| 
| [0,1; 1,2]
| 0,00001
| | | 3.263
| 
| [0,1; 1]
| 0,0025
| | | 3.264
| 
| [0,1; 1,2]
| 0,0005
| | | 3.265
| 
| -
| 0,0001
| | | Продолжение табл. 3.3
| | | №
задачи
| Уравнение
| Интервал
аргумента
[a; b]
| погрешность
ε
| | 3.266
| 
| -
| 0,0001
| | | 3.267
| 
| -
| 0,0001
| | | 3.268
| 
| [0,1; 2]
| 0,0001
| | | 3.269
| 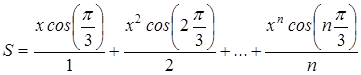
| [0,2; 1]
| 0,0001
| | | 3.270
| 
| [-0,5; 0,5]
| 0,0005
| | | 3.271
| 
| [1; 2]
| 0,0001
| | | | | | | | | | | | | | |
Раздел 4

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
Предпосылки, условия и движущие силы психического развития Предпосылки –это факторы. Факторы психического развития –это ведущие детерминанты развития чел. К ним относят: среду...
Анализ микросреды предприятия Анализ микросреды направлен на анализ состояния тех составляющих внешней среды, с которыми предприятие находится в непосредственном взаимодействии...
Типы конфликтных личностей (Дж. Скотт) Дж. Г. Скотт опирается на типологию Р. М. Брансом, но дополняет её. Они убеждены в своей абсолютной правоте и хотят, чтобы...
|
ТЕРМОДИНАМИКА БИОЛОГИЧЕСКИХ СИСТЕМ. 1. Особенности термодинамического метода изучения биологических систем. Основные понятия термодинамики. Термодинамикой называется раздел физики...
Травматическая окклюзия и ее клинические признаки При пародонтите и парадонтозе резистентность тканей пародонта падает...
Подкожное введение сывороток по методу Безредки. С целью предупреждения развития анафилактического шока и других аллергических реакций при введении иммунных сывороток используют метод Безредки для определения реакции больного на введение сыворотки...
|
|