Алгоритм расчета показателя РФН
Метод определения показателя РФН, изучаемый в данном пособии, заключается в анализе значимости структурных элементов и основан на теории графов и матриц. Краткие сведения о теории графов можно получить в [2].
1. Структурная схема исследуемой системы представляется в виде ориентированного графа  , где множество вершин , где множество вершин  составляют структурные элементы системы, а множество ребер составляют структурные элементы системы, а множество ребер  отображает связи между ними. Для геометрического представления ориентированное ребро отображает связи между ними. Для геометрического представления ориентированное ребро  показывается в виде дуги со стрелкой, направление которой совпадает с направлением потока энергии или информации между соединяемыми вершинами. Рассматриваются только связные графы, в которых для любой пары вершин показывается в виде дуги со стрелкой, направление которой совпадает с направлением потока энергии или информации между соединяемыми вершинами. Рассматриваются только связные графы, в которых для любой пары вершин 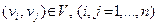 существует соединяющий их путь. существует соединяющий их путь.
2. Для построенного графа формируется матрица смежности  . Пусть структура системы содержит . Пусть структура системы содержит  вершин вершин 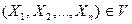 , соединенных , соединенных  ребрами ребрами  . Тогда получаем матрицу . Тогда получаем матрицу  размером размером  , которая состоит из нулей и единиц. Элемент матрицы , которая состоит из нулей и единиц. Элемент матрицы  , если граф содержит ребро , если граф содержит ребро  , направленное от вершины , направленное от вершины  к к  -му узлу. В противном случае принимается, что -му узлу. В противном случае принимается, что  . Число единичных элементов в матрице . Число единичных элементов в матрице  будет равно числу ребер. будет равно числу ребер.
3. Определяем матрицу  по следующей формуле: по следующей формуле:
 , ,
| (1)
| где  - матрица смежности. - матрица смежности.
4. Ранг элемента  определяется как сумма элементов определяется как сумма элементов  -й строки матрицы -й строки матрицы  : :

| (2)
| 5. Показатель РФН для структурного элемента  определяется выражением: определяется выражением:
 . .
| (3)
|
| Из формулы следует, что значение этого показателя определяется в процентном соотношении и нормализуется таким образом, что сумма показателей РФН всех элементов системы единична для любого исходного графа, т.е.
Такая нормализованная форма удобна для сравнительного анализа распределения функциональной нагрузки в системах различной сложности и с различными типами структуры.
6. Расчет общего показателя РФН группы элементов, входящих в определенную подсистему  , производится суммированием показателей РФН составляющих элементов. Например, если заданная группа , производится суммированием показателей РФН составляющих элементов. Например, если заданная группа  состоит из состоит из  элементов, тогда показатель РФН группы получается как сумма элементов, тогда показатель РФН группы получается как сумма  показателей: показателей:
 . .
| (4)
| Для оценки функциональной нагрузки целесообразно определить значение показателя РФН для элементов данной группы:
 . .
| (5)
| 7. Ранжирование элементов мехатронной системы производится на основе значений их показателей РФН и делается заключение о распределении функциональной нагрузки в исследуемой системе.
Пример
Представленную методику расчета показателя РФН рассмотрим на примере одного варианта системы управления робота "PUMA-560". Структура исследуемой системы (рис. 1) включает в себя как управляющую подсистему (контроллер движения), так и электромеханическую часть (электродвигатель и фотоимпульсные датчики обратной связи), которая будет неизменной при выполнении всего анализа.
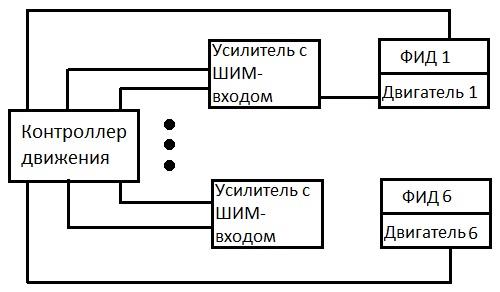
Рис.1. Структура системы управления робота «PUMA-560»
на основе контроллера движения
1. Построим граф  , представляющий структурную модель рассматриваемой системы (рис. 2). , представляющий структурную модель рассматриваемой системы (рис. 2).

Рис. 2. Граф, представляющий структурную модель системы
2. Для графа  составим матрицу смежности составим матрицу смежности  : :

Дальнейший расчет будет проводиться на компьютере с использованием языка Python[1] [3, 4] и библиотеки NumPy[2]. Python – это мощный и простой в использовании мультипарадигменный язык программирования позволяющий решать самые разные задачи от простых сценариев (скриптов) до сложных научно-технических задач. В состав Python входит большое число функциональных возможностей, известных как стандартная библиотека. Кроме того, Python допускает расширение как за счет ваших собственных библиотек, так и за счет библиотек, созданных сторонними разработчиками. Одним из таких расширений является NumPy – библиотека численных вычислений, позиционируемая как свободный и более мощный эквивалент системы математических вычислений Mathlab.
Для работы необходимо запустить программу IDLE[3]. Когда Python установлен в Windows, его можно найти в меню Пуск (Start). Набор пунктов меню может немного отличаться в зависимости от версии, но пункт IDLE запускает среду разработки с графическим интерфейсом, а пункт Python запускает сеанс работы с интерактивной командной оболочкой (консолью). Кроме того, здесь можно увидеть пункты вызова стандартного справочного руководства - Python Manuals.
Чтобы использовать функции NumPy нужно импортировать соответствующую библиотеку, выполнив команду:
Введем матрицу  в компьютер: в компьютер:
| >>> A = numpy.matrix([[0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]])
|
3. Определим матрицу  по формуле (1): по формуле (1):
4. Определим ранг структурных элементов по формуле (2):
| >>> X = numpy.zeros([19, 1]) # создаем вектор X
>>> for i in range(0, 19): for j in range(0, 19): X[i] += A[i, j]
>>> print X # вывод на экран вектора X
|
5. Определим показатель РФН:
| >>> S = numpy.sum(X) # cумма элементов вектора X
>>> I = zeros([19, 1]) # создаем вектор I
>>> for i in range(0, 19): I[i] = (X[i] * 100)/S
>>> print I # вывод на экран вектора I
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Предпосылки, условия и движущие силы психического развития Предпосылки –это факторы. Факторы психического развития –это ведущие детерминанты развития чел. К ним относят: среду...
Анализ микросреды предприятия Анализ микросреды направлен на анализ состояния тех составляющих внешней среды, с которыми предприятие находится в непосредственном взаимодействии...
Типы конфликтных личностей (Дж. Скотт) Дж. Г. Скотт опирается на типологию Р. М. Брансом, но дополняет её. Они убеждены в своей абсолютной правоте и хотят, чтобы...
|
Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
Краткая психологическая характеристика возрастных периодов.Первый критический период развития ребенка — период новорожденности Психоаналитики говорят, что это первая травма, которую переживает ребенок, и она настолько сильна, что вся последующая жизнь проходит под знаком этой травмы...
РЕВМАТИЧЕСКИЕ БОЛЕЗНИ Ревматические болезни(или диффузные болезни соединительно ткани(ДБСТ))— это группа заболеваний, характеризующихся первичным системным поражением соединительной ткани в связи с нарушением иммунного гомеостаза...
|
|

 , где множество вершин
, где множество вершин  составляют структурные элементы системы, а множество ребер
составляют структурные элементы системы, а множество ребер  отображает связи между ними. Для геометрического представления ориентированное ребро
отображает связи между ними. Для геометрического представления ориентированное ребро  показывается в виде дуги со стрелкой, направление которой совпадает с направлением потока энергии или информации между соединяемыми вершинами. Рассматриваются только связные графы, в которых для любой пары вершин
показывается в виде дуги со стрелкой, направление которой совпадает с направлением потока энергии или информации между соединяемыми вершинами. Рассматриваются только связные графы, в которых для любой пары вершин 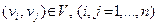 существует соединяющий их путь.
существует соединяющий их путь. . Пусть структура системы содержит
. Пусть структура системы содержит  вершин
вершин 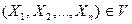 , соединенных
, соединенных  ребрами
ребрами  . Тогда получаем матрицу
. Тогда получаем матрицу  размером
размером  , которая состоит из нулей и единиц. Элемент матрицы
, которая состоит из нулей и единиц. Элемент матрицы  , если граф содержит ребро
, если граф содержит ребро  , направленное от вершины
, направленное от вершины  к
к  -му узлу. В противном случае принимается, что
-му узлу. В противном случае принимается, что  . Число единичных элементов в матрице
. Число единичных элементов в матрице  по следующей формуле:
по следующей формуле: ,
,
 -й строки матрицы
-й строки матрицы 
 .
.

 , производится суммированием показателей РФН составляющих элементов. Например, если заданная группа
, производится суммированием показателей РФН составляющих элементов. Например, если заданная группа  состоит из
состоит из  элементов, тогда показатель РФН группы получается как сумма
элементов, тогда показатель РФН группы получается как сумма  .
.
 .
.

 , представляющий структурную модель рассматриваемой системы (рис. 2).
, представляющий структурную модель рассматриваемой системы (рис. 2).




