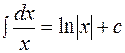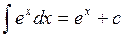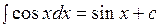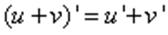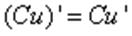Основные свойства неопределенных интегралов
Таблица очков
Таблица производных
Основные свойства неопределенных интегралов 1. Постоянную можно выносить за знак интеграла. Если функция f (x) имеет первообразную на промежутке X, и k – число, то
2. Интеграл суммы равен сумме интегралов. Если функции f (x) и g (x) имеют первообразные на промежутке X, то
3. Производная от интеграла равна подынтегральной функции. Если функция f (x) имеет первообразную на промежутке X, то для внутренних точек этого промежутка:
4. Интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования. Если функция f (x) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:
Таблица неопределенных интегралов
Правила вычисления производной 1. Производная суммы двух функций:
2. Производная произведения постоянной и функции:
3. Производная произведения двух функций:
4. Производная частного двух функций:
5. Производная сложной функции:
|


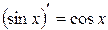
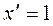







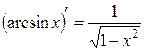


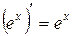





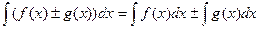




 ; α ≠ -1
; α ≠ -1