Регулярная точка
Точка поверхности (7) называется регулярной точкой, если при некотором параметрическом задании поверхности в достаточно малой окрестности рассматриваемой точки а) существуют непрерывные частные производные б) Перечисленные условия обеспечивают существование и линейную независимость векторов
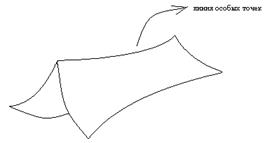
Точка, не являющаяся регулярной, называется особой. Так, особым точкам соответствуют ребра, вершины и т.д.
Простой кусок поверхности, ограниченный регулярной замкнутой кривой, называется регулярным, если все его внутренние точки регулярные. Регулярной (кусочно-гладкой) поверхностью называется двусторонняя простая (замкнутая или незамкнутая) поверхность, составленная из конечного числа регулярных кусков с общими регулярными дугами и точками. Кусочно-гладкая поверхность квадрируема. К понятию кусочно-гладкой поверхности прибегают, если на всей поверхности не может быть введена единая параметризация, имеются линии особых точек и т.д. Примеры кусочно-гладких поверхностей: поверхность цилиндра, поверхность параллелепипеда.
Касательная плоскость и нормаль к поверхности. Пусть Производные берутся при Единичный вектор нормали к поверхности Направление вектора В некоторой окрестности каждой регулярной точки кусочно-гладкой поверхности существует непрерывное векторное поле нормалей. Можно сказать: поверхность является гладкой, если обладает непрерывно изменяющейся нормалью. Кусочно-гладкая поверхность составлена из гладких кусков. В каждой регулярной точке двусторонней поверхности, заданной уравнением
В случае замкнутой поверхности координаты
Поверхностный интеграл I рода есть скалярный поверхностный интеграл
Интеграл (11) не зависит от выбора стороны поверхности.
Поверхностный интеграл II рода есть скалярный поверхностный интеграл
Заметим:
Вспомните условия существования интегралов (11) и (12). Достаточно:
|


 .
. и
и  , направленных соответственно по касательным к координатным линиям: линии
, направленных соответственно по касательным к координатным линиям: линии  и линии
и линии  на поверхности, проходящим через точку
на поверхности, проходящим через точку  .
.
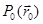 - регулярная точка поверхности;
- регулярная точка поверхности;  . В этой точке
. В этой точке  ! касательная плоскость к поверхности, определяемая уравнением
! касательная плоскость к поверхности, определяемая уравнением  (смешанное произведение)
(смешанное произведение) .
. в точке
в точке 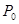 :
: 
 называется направлением положительной нормали в точке
называется направлением положительной нормали в точке  (направление вектора
(направление вектора  (направление вектора
(направление вектора  , можно определить векторный элемент поверхности (векторный элемент площади, вектор площадки):
, можно определить векторный элемент поверхности (векторный элемент площади, вектор площадки): (10)
(10) на поверхности обычно упорядочивают так, чтобы направление вектора
на поверхности обычно упорядочивают так, чтобы направление вектора  (направление положительной нормали к поверхности) было внешним по отношению к телу, ограниченному данной поверхностью.
(направление положительной нормали к поверхности) было внешним по отношению к телу, ограниченному данной поверхностью. . (11)
. (11) . (12)
. (12) . (13)
. (13) и компоненты
и компоненты  - кусочно – непрерывные.
- кусочно – непрерывные.


