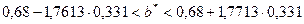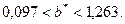Примеры решения задач по парной регрессии.
Задача7. Определить минимальную активность золотой фольги, используемой при оценке спектра нейтронов, которую можно определить методом b-g -совпадений и оценить фон случайных совпадений. t << Rb; d =2 см; детекторы: торцевой b счетчик с окошком, толщиной 10 мг/см2, гамма-детектор- NaI(Tl) 40*40; Tизм =103 с; расстояние источник детектор 1 см. mNaI(0.412) = 0.1г/см2 Ответ Q = 3.7102 Бк Задача 8. Определить поток тепловых нейтронов для получения минимально измеряемой активности фольги методом b-g совпадений Qmin = 102 Бк. sакт = 96 барн, T1/2 =2.7 сут.; Условие: hSакт <<1 Þ 0.05, время облучения Tобл = 104с. Dфольги = 2 см Sакт = h =
Активность к концу облучения Q = lNAu = lShjSактTобл =- j = Задача 9 Оценить скорость счета n КД с 238U c S = 102 см2 на расстоянии 20 см от источника 252Cf активностью Q =106 н\с Толщина слоя урана >> Rf = 10-2 г/см2 c(E) µ E1/2exp(-E/T) T = 1,4 МэВ sэфф = 0.59 б Eэфф = 1,5 МэВ e = 2SэффR/2 = 0,59*0,6*19*10-2/238 = 2,810-4 ed = eS = 2,810-2см2 k = n = [Qed/4pR2 ]k = 106*0,55*2,810-2/12,6*4102 = 3 имп/с (без учёта порога) Задача 10. Определить поток тепловых нейтронов для получения минимально измеряемой активности фольги методом b-g совпадений Qmin = 102 Бк. sакт = 96 барн, T1/2 =2.7 сут.; Условие: hSакт <<1 Þ 0.05, время облучения Tобл = 104с. Dфольги = 2 см Sакт = 61023*9,610-231,93101/1,97102 = 5,6 см-1 h = 910-3 см
Активность к концу облучения Q = lNAu = lShjSактTобл = ljSакт TоблpD2h/4 102 = (0,69/2,4*3,6104)j 5,6*104*3,14*910-3 j = 7,7103 н/см2с Задача 11. Оценить возможность измерения дозы ТДД при P = 1*1017дел/всп. rU = 8,2 см Экспериментатор на R =0,7 м от сборки Dn(1МэВ)/Fn = 210-11 Гр/нейт/см2 (ОБЭ на этом уровне»3) Баланс: из нейтронов один на деление и h-1»1 утекает Полное число нейтронов утечки Ln = (h-1)P = 11017. В стекле регистрируются только осколки деления с эффективностью 0,3 Оценка дозы быстрых нейтронов по твёрдотельному детектору уран-стекло при флюенсе 1012 н/см2, просматривается S =10-2 см2, эффективная толщина слоя 3мг/см2, сечение деления при 1МэВ - 0,5 барн Плотность дырок n при эффективности 0,3 и S =10-2 см2 n = 0,3*1012*0,510-24*61023 *310-3*10-2 /2,38102 = 104 дырок/мм2
Примеры решения задач по парной регрессии.
1 задача из базы которая с сайта!:: Задача 1. Исследуя спрос на продукцию фирмы, аналитический отдел собрал данные по 20 торговым точкам компании и представил их в виде: ln y = 6,8 – 0,6 ln x + ε, (2,7) (-2,8) где y – объем спроса, x – цена единицы продукции. В скобках приведены фактически значения t – критерия. Ранее предполагалось, что увеличение цены на 1% приводит к уменьшению спроса на 1,2%. Можно ли утверждать, что приведенные результаты подтверждают это предположение? Решение: Уравнение регрессии в прологарифмированном виде. Судя по форме записи, уравнение имеет степенной вид и записывается так:
Надо проверить предположение о том, что эластичность спроса по цене равна –1,2. В степенной зависимости эластичность равна показателю степени b, поэтому оценка эластичности равна –0,6. Таким образом, задача сводится к проверке статистической гипотезы (нуль - гипотезы) H0:b=-1,2 против альтернативной H1:b≠-1,2. Критическая область двусторонняя, поэтому проверка гипотезы может быть заменена построением доверительного интервала для b и, если проверяемое значение b=-1,2 попадает в него, то нуль-гипотеза не отклоняется; в противном случае принимается альтернативная гипотеза. Интервал строится по формуле: -0,6- mb · tтаб < b < -0,6+ mb · tтабл. Определим стандартную ошибку параметра b из формулы: mb = Для определения tтабл зададим уровень значимости, равный 0,05, следовательно: tтабл (α; n-2) = tтабл (0,05;18) = 2,1 (используем таблицу критических точек распределения Стьюдента для двустороннего α=0,05). Доверительный интервал равен: -0,6-0,2143·2,1 < b < -0,6+0,2143·2,1 или -1,05 < b < -0,15. Значение, равное –1,2, в интервал не попадает, следовательно, предположение о значении коэффициента эластичности на уровне значимости 0,05 следует отклонить. Однако, если задать значимость на уровне 0,01, то tтабл=2,88, и интервал будет таким: -1,217 < b < 0,017 Следовательно, на уровне значимости 0,01 первоначальное предположение не может быть отклонено, поскольку значение –1,2 попадает в доверительный интервал. Можно проверить статистическую гипотезу напрямую, вычислив t –статистику для разницы между гипотетическим и вычисленным значениями b:
Сравним полученную статистику по абсолютной величине с критическим значением на заданном уровне значимости. На уровне α=0,05:
Нуль-гипотеза отклоняется, эластичность спроса по цене не может быть равна –1,2. На уровне α=0,01:
нуль-гипотеза не отклоняется, эластичность может быть равна –1,2. ■
2 задача из базы которая с сайта!:: Задача 2. Для двух видов продукции А и Б зависимости удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
Сравнить эластичность затрат по каждому виду продукции при x =50 и определить объемы продукции обоих видов, при котором эластичности будут одинаковы. Решение Регрессионная зависимость для продукции А является полулогарифмической, и для вычисления эластичности воспользуемся формулой: ЭА = Для продукции Б регрессионная зависимость является степенной, где коэффициент эластичности равен показателю степени при любых значениях независимой переменной, следовательно: ЭБ = 0,3. Теперь определим точку, в которой эластичности по обоим видам продукции одинаковы. Для продукции Б подходит любой объем, т.к. эластичность постоянна, а для определения объема выпуска продукции Б составим и решим уравнение:
отсюда xА = 4,3 единиц. Таким образом, при объеме производства продукции А, равном 4,3, эластичности удельных постоянных расходов обоих видов продукции по объему выпуска одинаковы и равны 0,3. ■
3 задача из базы с сайта:: Задача 3. Пусть имеется уравнение парной регрессии: y = 5 - 6x + ε, построенное по 15 наблюдениям. При этом r = –0,7. Определить доверительный интервал, в который с вероятностью 0,99 попадает коэффициент регрессии. Решение. Для построения доверительного интервала необходимо знать стандартную ошибку mb коэффициента регрессии. Однако она не задана, и нужно определить ее косвенным путем. Для этого воспользуемся тем, что в парной регрессии существует связь между t- и F-статистиками: tb = а F - статистику определим так: F = tb = (берем минус, так как знак оцененного коэффициента b отрицательный). mb = Доверительный интервал имеет вид (tтабл(0,01;13)=3,01): -6 – 1,7·3,01 < b < -6 + 1,7·3,01 или -11,11 < b < -0,89. ■
4 задача из базы с сайта:: Задача 4. Уравнение регрессии потребления материалов от объема производства, построенное по 15 наблюдениям, имеет вид: y = 5 + 5x + ε (4,0) В скобках – фактическое значение t-критерия. Определить коэффициент детерминации для этого уравнения. Решение: Зная t-критерий для коэффициента регрессии, вычислим F - критерий для данного уравнения: F = tb2 = 42 = 16. Далее воспользуемся выражением для F через
■
9,10,14 из базы с сайта(типовые):: Задача 5. По совокупности 18 предприятий торговли изучается зависимость между ценой x на некоторый товар и прибылью y торгового предприятия. При оценке регрессионной модели были получены следующие результаты:
Определить индекс корреляции и фактическое значение F-критерия, а также статистическую значимость уравнения регрессии. Построить таблицу дисперсионного анализа. Решение: В условиях задачи n=18; остаточная СКО равна 23, а общая СКО – 35. Расчет индекса корреляции: R =
Фактическое значение F-критерия: F = При проверке статистической значимости уравнения в целом воспользуемся F-критерием и сравним его с критическим значением, задавшись уровнем значимости 0,05. Табличное (критическое) значение при этом равно: Fтабл (0,05;1;18-2) = 4,49. Поскольку фактическое значение, равное 8,35, больше критического, нуль-гипотезу о статистической незначимости уравнения регрессии следует отклонить, и уравнение на уровне α=0,05 является значимым; статистическая связь между y и x считается доказанной. Однако, если задать α=0,01, то: Fкр = Fтабл (0,01;1;16)=8,53, и в этом случае нуль-гипотезу отклонить нельзя, на уровне α=0,01 уравнение не значимо. Для построения таблицы дисперсионного анализа определим из балансового уравнения величину факторной СКО:
Поскольку мы имеем дело с парной регрессионной зависимостью, число степеней свободы факторной СКО принимаем равным единице. С учетом этих условий таблица дисперсионного анализа выглядит следующим образом:
5,6,7 задачи из базы с сайта(типовые):: Задача 7. Для следующих уравнений регрессии: а) б) в) г) определить коэффициенты эластичности при значении фактора, равном 85. Решение. а) Уравнение регрессии является линейным, поэтому коэффициент эластичности равен б) Здесь имеем дело с полулогарифмической зависимостью: в) Это преобразованная (путем логарифмирования) степенная зависимость; её коэффициент эластичности постоянен и равен показателю степени, т.е. 0,0024. г) В данном случае зависимость показательная (или экспоненциальная), в преобразованном виде логарифмируется только зависимая переменная. В любой из трех форм записи экспоненциальной регрессии коэффициент эластичности равен произведению коэффициента при факторе на значение самого фактора, т.е. ■ Задача 8. Имеются следующие исходные данные (n =24): - - корреляция между х и у отрицательная; - значение критерия Фишера для линейной регрессии составило 17. Определить: - коэффициент детерминации; - уравнение линейной регрессии; - средний по выборке коэффициент эластичности (для линейной зависимости); - доверительный интервал прогноза с вероятностью 0,9 при значении фактора на 15% выше среднего уровня.
Решение. 1. Коэффициент детерминации определяем из выражения:
2. Построение уравнения линейной регрессии начинаем с вычисления коэффициента регрессии с помощью выражения:
Учитывая, что корреляция отрицательная, получим:
Значения стандартных отклонений по каждой переменной найдем с использованием коэффициентов вариации:
и аналогично для у:
Таким образом,
Свободный член определим из выражения:
Запишем уравнение линейной регрессии:
3. Средний по выборке коэффициент эластичности находим из выражения для линейной зависимости:
4. Доверительный интервал прогноза по линейному уравнению регрессии построим по выражению:
Серединой доверительного интервала является прогнозное значение зависимой переменной, полученное при значении фактора, равном
Отсюда прогнозное значение получаем подстановкой в уравнение регрессии:
Табличное значение статистики Стьюдента:
Стандартная ошибка прогноза индивидуального значения определяется по выражению:
Рассчитаем отдельные компоненты этого выражения: - - поскольку - поскольку
Отсюда стандартная ошибка равна
Теперь строим доверительный интервал прогноза:
13 задача из базы с сайта::Задача 9. По выборке из 16 предприятий холдинга была построена следующая регрессионная зависимость объема продаж у (тыс. руб.) от расходов на рекламу х (тыс. руб.): - Задание: - определить коэффициент корреляции; - построить таблицу дисперсионного анализа для оценки значимости уравнения регрессии в целом; - оценить значимость коэффициента регрессии; - построить доверительный интервал для коэффициента регрессии с вероятностью 0,9 и сделать вывод. Решение. 1. Коэффициент корреляции находим с помощью формулы:
2. Для построения таблицы дисперсионного анализа найдем значения различных СКО в балансовом выражении (13): Общ.СКО= Факт.СКО=Общ.СКО Ост.СКО=Общ.СКО-Факт.СКО=1008,6-233,35=775,25. Отсюда строим таблицу:
3. Для нахождения стандартной ошибки оценки коэффициента регрессии можно воспользоваться формулой:
или формулой:
откуда
4. Значимость коэффициента регрессии определяем через t - критерий Стьюдента:
Проверка нуль - гипотезы 5. Доверительный интервал для коэффициента регрессии на уровне значимости 0,1 строим по соответствующей формуле:
или
Он накрывает неизвестное значение параметра с вероятностью 0,9; границы интервала имеют одинаковые знаки, поэтому на уровне 0,1 параметр статистически значим.
|

 Tобл << T1/2
Tобл << T1/2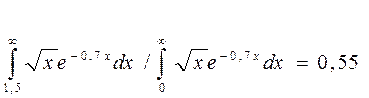
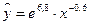
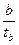 =
= 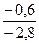 = 0,2143
= 0,2143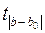 =
= 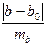 =
=  = 2,8.
= 2,8.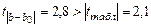 ;
;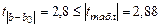 ;
; = 15 + 8·lnx,
= 15 + 8·lnx, = 25x0,3.
= 25x0,3.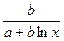 =
= 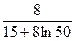 = 0,173.
= 0,173.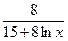 = 0,3;
= 0,3; ,
, · (15-2) = 12,5;
· (15-2) = 12,5;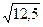 = –3,53;
= –3,53;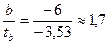 ;
; , из которого определим коэффициент детерминации при n=15:
, из которого определим коэффициент детерминации при n=15: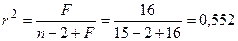 .
.
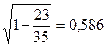 ; R2 = 0,343.
; R2 = 0,343.
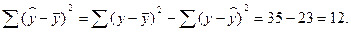
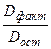
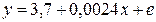
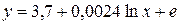
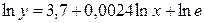
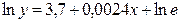
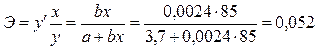 .
.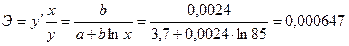 .
.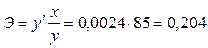 .
.
 , откуда
, откуда 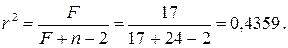
 , откуда
, откуда  .
.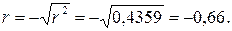
 , откуда
, откуда 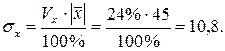


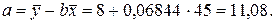
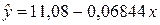 .
.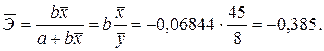
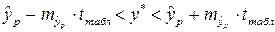

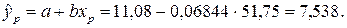
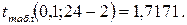
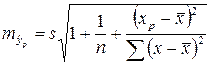
 ;
;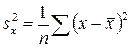 , можно записать
, можно записать 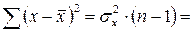
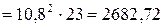 ;
;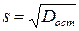 , то
, то 
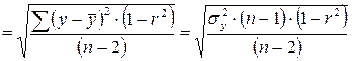 (по аналогии с предыдущим); тогда
(по аналогии с предыдущим); тогда 
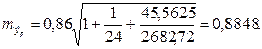

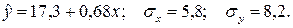
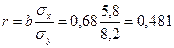



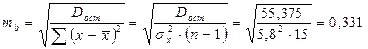
 , где
, где 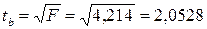

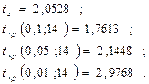
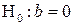 против альтернативной
против альтернативной  показывает, что параметр b значим на уровне 0,1 и не значим на уровнях 0,05 и 0,01.
показывает, что параметр b значим на уровне 0,1 и не значим на уровнях 0,05 и 0,01.