Преобразование параллельно соединенных ветвей
Пусть имеем схему на рис. 6,а.
Согласно закону Ома для участка цепи с источником ЭДС
где Тогда
причем со знаком “+” в (4) записываются ЭДС 3. Взаимные преобразования “треугольник-звезда”
Преобразовать треугольник в звезду – значит заменить три сопротивления, соединенных в треугольник между какими-то тремя узлами, другими тремя сопротивлениями, соединенными в звезду между теми же точками. При этом на участках схемы, не затронутых этими преобразованиями, токи должны остаться неизменными. Без вывода запишем формулы эквивалентных преобразований
Литература
Контрольные вопросы и задачи
Ответ:
Ответ:
Ответ: | ||||||||||||||||
| Лекция N 10. Анализ цепей с индуктивно связанными элементами. |
Электрические цепи могут содержать элементы, индуктивно связанные друг с другом. Такие элементы могут связывать цепи, электрически (гальванически) разделенные друг от друга.
В том случае, когда изменение тока в одном из элементов цепи приводит к появлению ЭДС в другом элементе цепи, говорят, что эти два элемента индуктивно связаны, а возникающую ЭДС называют ЭДС взаимной индукции. Степень индуктивной связи элементов характеризуется коэффициентом связи
где М – взаимная индуктивность элементов цепи (размерность – Гн);
Пусть имеем две соосные катушки в общем случае с ферромагнитным сердечником (см. рис. 1). На рис. 1 схематично показана картина магнитного поля при наличии тока i1 в первой катушке (направление силовых линий магнитного потока определяется по правилу правого буравчика). Витки первой катушки сцеплены с магнитным потоком самоиндукции Ф11, а витки второй катушки – с магнитным потоком взаимной индукции Ф21, который отличается от Ф11 (Ф21< Ф11) за счет потоков рассеяния. По определению
Если теперь наоборот пропустить ток i2 по второй катушке, то соответственно получим
При этом
Следует отметить, что коэффициент связи мог бы быть равным 1, если бы
Рассмотрим цепь переменного тока на рис. 2, в которую последовательно включены две катушки индуктивности
Тогда, если в цепи протекает гармонически изменяющийся ток
а во второй –
Катушки можно включить так, что ЭДС самоиндукции будет суммироваться с ЭДС взаимоиндукции; при переключении одной из катушек ЭДС взаимоиндукции будет вычитаться из ЭДС самоиндукции. Один из зажимов каждой катушки на схеме помечают, например точкой или звездочкой. Этот знак означает, что при увеличении, например, тока в первой катушке, протекающего от точки, во второй катушке индуцируется ЭДС взаимоиндукции, действующая от другого конца к точке. Различают согласное и встречное включения катушек. При согласном включении токи в катушках одинаково ориентированы по отношению к их одноименным зажимам. При этом ЭДС само- и взаимоиндукции складываются – случай, показанный на рис. 2. При встречном включении катушек токи ориентированы относительно одноименных зажимов различно. В этом случае ЭДС само- и взаимоиндукции вычитаются. Таким образом, тип включения катушек (согласное или встречное) определяются совместно способом намотки катушек и направлении токов в них. Перейдя к комплексной форме записи (7) и (8), получим
где Для определения тока в цепи на рис. 2 запишем
откуда
|


 ,
,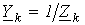 .
. ,
,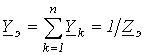 ;
;
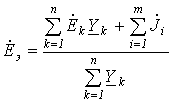 ,
,
 и ток
и ток 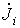 , если они направлены к тому же узлу, что и ЭДС
, если они направлены к тому же узлу, что и ЭДС  ; в противном случае они записываются со знаком “-”.
; в противном случае они записываются со знаком “-”. В ряде случаев могут встретиться схемы, соединения в которых нельзя отнести ни к последовательному, ни к параллельному типу (см. рис. 7). В таких случаях преобразования носят более сложный характер: преобразование треугольника в звезду и наоборот.
В ряде случаев могут встретиться схемы, соединения в которых нельзя отнести ни к последовательному, ни к параллельному типу (см. рис. 7). В таких случаях преобразования носят более сложный характер: преобразование треугольника в звезду и наоборот.
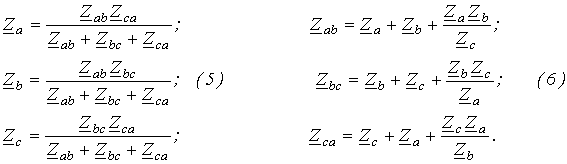

 и параметры всех ее элементов, качественно построить векторную диаграмму токов и топографическую диаграмму потенциалов для нее.
и параметры всех ее элементов, качественно построить векторную диаграмму токов и топографическую диаграмму потенциалов для нее. 
 .
.  .
. ;
;  ;
;  .
. ,
,  и
и 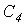 .
.  ;
; 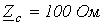 ;
;  .
. ,
,
 и
и 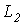 -собственные индуктивности этих элементов.
-собственные индуктивности этих элементов. Слеует отметить, что всегда к<1.
Слеует отметить, что всегда к<1. ;
;
 .
.
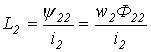 ;
;
 .
.
 .
.
 и
и  , то есть когда весь поток, создаваемый одной катушкой, полностью пронизывал бы витки другой катушки. Практически даже различные витки одной и той же катушки пронизываются разными потоками. Поэтому с учетом рассеяния
, то есть когда весь поток, создаваемый одной катушкой, полностью пронизывал бы витки другой катушки. Практически даже различные витки одной и той же катушки пронизываются разными потоками. Поэтому с учетом рассеяния  и
и  . В этой связи
. В этой связи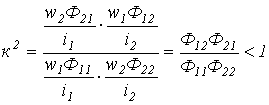 .
. При изменении тока i в цепи в катушках индуцируются ЭДС само- и взаимоиндукции. При этом ЭДС взаимной индукции должна по закону Ленца иметь такое направление, чтобы препятствовать изменению потока взаимной индукции.
При изменении тока i в цепи в катушках индуцируются ЭДС само- и взаимоиндукции. При этом ЭДС взаимной индукции должна по закону Ленца иметь такое направление, чтобы препятствовать изменению потока взаимной индукции. , то в первой катушке индуцируется ЭДС
, то в первой катушке индуцируется ЭДС ,
,
 .
.
 ;
;
 ,
,
 - сопротивление взаимоиндукции (Ом).
- сопротивление взаимоиндукции (Ом). ,
,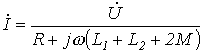 .
.


