Составление матричных соотношений при наличии ветвей с идеальными источниками
В цепи могут иметь место ветви, содержащие только идеальные источники ЭДС или тока. При записи уравнений без использования матричных соотношений такие ветви не вносят каких-либо особенностей в их составление. Однако, если уравнения записываются по второму закону Кирхгофа в матричной форме или используется матричная форма контурных уравнений, то в матрице сопротивлений ветвей Z ветвям, содержащим идеальные источники тока, будут соответствовать диагональные элементы
Здесь идеальный источник тока Может быть другой случай, когда уравнения в матричной форме записываются по первому закону Кирхгофа или используется матричная форма узловых уравнений, а в цепи имеют место ветви, содержащие только идеальные источники ЭДС. Для таких ветвей соответствующие им диагональные элементы матрицы Y будут равны Здесь участок исходной цепи (см. рис. 4,а) содержит ветвь с идеальным источником ЭДС
Контрольные вопросы и задачи
Ответ:
.
| |||||||||||
| Лекция N 12. Методы расчета, основанные на свойствах линейных цепей. |
Выбор того или иного метода расчета электрической цепи в конечном итоге определяется целью решаемой задачи. Поэтому анализ линейной цепи не обязательно должен осуществляться с помощью таких общих методов расчета, как метод контурных токов или узловых потенциалов. Ниже будут рассмотрены методы, основанные на свойствах линейных электрических цепей и позволяющие при определенных постановках задач решить их более экономично.
Метод наложения
Данный метод справедлив только для линейных электрических цепей и является особенно эффективным, когда требуется вычислить токи для различных значений ЭДС и токов источников в то время, как сопротивления схемы остаются неизменными.
Данный метод основан на принципе наложения (суперпозиции),который формулируется следующим образом: ток в k – й ветви линейной электрической цепи равен алгебраической сумме токов, вызываемых каждым из источников в отдельности.
Аналитически принцип наложения для цепи, содержащей n источников ЭДС и m источников тока, выражается соотношением
Здесь Входные и взаимные проводимости можно определить экспериментально или аналитически, используя их указанную смысловую трактовку, при этом Аналогично определяются коэффициенты передачи тока Доказательство принципа наложения можно осуществить на основе метода контурных токов. Если решить систему уравнений, составленных по методу контурных токов, относительно любого контурного тока, например
где Каждая из ЭДС в (2) представляет собой алгебраическую сумму ЭДС в ветвях i–го контура. Если теперь все контурные ЭДС в (2) заменить алгебраическими суммами ЭДС в соответствующих ветвях, то после группировки слагаемых получится выражение для контурного тока Таким образом, при определении токов ветвей при помощи метода наложения следует поочередно оставлять в схеме по одному источнику, заменяя остальные их внутренними сопротивлениями, и рассчитать составляющие искомых токов в этих схемах. После этого полученные результаты для соответствующих ветвей суммируются – это и будут искомые токи в ветвях исходной цепи. В качестве примера использования метода наложения определим ток во второй ветви схемы на рис. 1,а.
Принимая источники в цепи на рис. 1,а идеальными и учитывая, что у идеального источника ЭДС внутреннее сопротивление равно нулю, а у идеального источника тока – бесконечности, в соответствии с методом наложения приходим к расчетным схемам на рис. 1,б…1,г. В этих цепях
где Таким образом,
Учитывая, что в структуре пассивного четырехполюсника не содержится источников энергии, на основании принципа наложения для состояния ключа в положении “1” можно записать
При переводе ключа в положение “2” имеем
Тогда, вычитая из уравнения (3) соотношение (5), а из (4)-(6), получим
откуда искомые проводимости
|

 . Поэтому при наличии таких ветвей исходная схема перед составлением уравнений должна быть подвергнута соответствующему преобразованию, иллюстрируемому рис. 3.
. Поэтому при наличии таких ветвей исходная схема перед составлением уравнений должна быть подвергнута соответствующему преобразованию, иллюстрируемому рис. 3.
 (см. рис. 3,а) включен между узлами k и n. Подключение к узлам l и m по два одинаковых по величине и противоположно направленных источника тока
(см. рис. 3,а) включен между узлами k и n. Подключение к узлам l и m по два одинаковых по величине и противоположно направленных источника тока 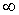 . Поэтому при наличии таких ветвей исходную схему перед составлением уравнений необходимо подвергнуть преобразованию, поясняемому рис. 4.
. Поэтому при наличии таких ветвей исходную схему перед составлением уравнений необходимо подвергнуть преобразованию, поясняемому рис. 4.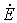 . Включение в каждую ветвь, соединенную с узлом n, источника с ЭДС, равной
. Включение в каждую ветвь, соединенную с узлом n, источника с ЭДС, равной  ) трансформировать исходную цепь в схему, представленную на рис. 4,в.
) трансформировать исходную цепь в схему, представленную на рис. 4,в.
 ;
;  ;
;  ;
; 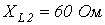 ;
;  ;
;  . Приняв, что дерево образовано ветвью 1, составить контурные уравнения в матричной форме и определить токи ветвей.
. Приняв, что дерево образовано ветвью 1, составить контурные уравнения в матричной форме и определить токи ветвей. 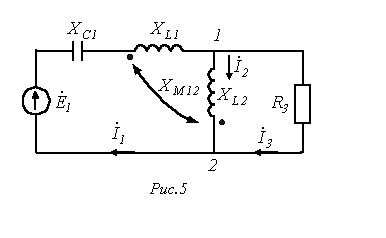


 .
.
 ;
;

 .
.
 - комплекс входной проводимости k – й ветви, численно равный отношению тока к ЭДС в этой ветви при равных нулю ЭДС в остальных ветвях;
- комплекс входной проводимости k – й ветви, численно равный отношению тока к ЭДС в этой ветви при равных нулю ЭДС в остальных ветвях;  - комплекс взаимной проводимости k – й и i– й ветвей, численно равный отношению тока в k – й ветви и ЭДС в i– й ветви при равных нулю ЭДС в остальных ветвях.
- комплекс взаимной проводимости k – й и i– й ветвей, численно равный отношению тока в k – й ветви и ЭДС в i– й ветви при равных нулю ЭДС в остальных ветвях.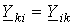 , что непосредственно вытекает из свойства взаимности (см. ниже).
, что непосредственно вытекает из свойства взаимности (см. ниже). , которые в отличие от проводимостей являются величинами безразмерными.
, которые в отличие от проводимостей являются величинами безразмерными. , то получим
, то получим ,
,
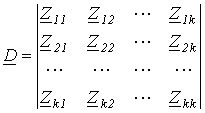 - определитель системы уравнений, составленный по методу контурных токов;
- определитель системы уравнений, составленный по методу контурных токов; 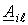 - алгебраическое дополнение определителя
- алгебраическое дополнение определителя  .
.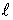 -й контур, т.е. контурный ток
-й контур, т.е. контурный ток  h-й ветви, то принцип наложения справедлив для токов
h-й ветви, то принцип наложения справедлив для токов 
 ;
;  ;
;  ,
, ;
; 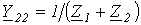 ;
;  .
. .
. В качестве другого примера использования метода определим взаимные проводимости
В качестве другого примера использования метода определим взаимные проводимости  и
и  в цепи на рис. 2, если при переводе ключа в положение 1 токи в первой и второй ветвях соответственно равны
в цепи на рис. 2, если при переводе ключа в положение 1 токи в первой и второй ветвях соответственно равны  и
и 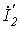 , а при переводе в положение 2 -
, а при переводе в положение 2 -  и
и  .
. ;
;
 .
.
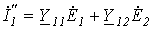 ;
;
 ..
..
 ;
; ,
, ;
;  .
.


