Характеристическое сопротивление и коэффициент распространения симметричного четырехполюсника
В электросвязи широко используется режим работы симметричного четырехполюсника, при котором его входное сопротивление равно нагрузочному, т.е.
Это сопротивление обозначают как
называется режимом согласованной нагрузки. В указанном режиме для симметричного четырехполюсника
Разделив соотношение (13) на (14), получаем уравнение
решением которого является
С учетом (15) уравнения (13) и (14) приобретают вид
Таким образом,
где Одному неперу соответствует затухание по напряжению или току в е=2,718… раз, а по мощности, поскольку для рассматриваемого случая Запишем уравнение симметричного четырехполюсника с использованием коэффициента распространения. По определению
Тогда
Решая (17) и (18) относительно
Учитывая, что
и
получаем уравнения четырехполюсника, записанные через гиперболические функции:
Литература
Контрольные вопросы и задачи
Ответ:
Определить параметры Т-образной схемы замещения. Ответ:
Определить, при каком сопротивлении нагрузки входное сопротивление четырехполюсника будет равно нагрузочному сопротивлению. Ответ: | |||||||||||
| Лекция N 15. Электрические фильтры. |
Электрическим фильтром называется четырехполюсник, устанавливаемый между источником питания и нагрузкой и служащий для беспрепятственного (с малым затуханием) пропускания токов одних частот и задержки (или пропускания с большим затуханием) токов других частот.
Диапазон частот, пропускаемых фильтром без затухания (с малым затуханием), называется полосой пропусканияили полосой прозрачности;диапазон частот, пропускаемых с большим затуханием, называется полосой затуханияили полосой задерживания.Качество фильтра считается тем выше, чем ярче выражены его фильтрующие свойства, т.е. чем сильнее возрастает затухание в полосе задерживания.
В качестве пассивных фильтров обычно применяются четырехполюсники на основе катушек индуктивности и конденсаторов. Возможно также применение пассивных RC-фильтров, используемых при больших сопротивлениях нагрузки.
Фильтры применяются как в радиотехнике и технике связи, где имеют место токи достаточно высоких частот, так и в силовой электронике и электротехнике.
Для упрощения анализа будем считать, что фильтры составлены из идеальных катушек индуктивности и конденсаторов, т.е. элементов соответственно с нулевыми активными сопротивлением и проводимостью. Это допущение достаточно корректно при высоких частотах, когда индуктивные сопротивления катушек много больше их активных сопротивлений (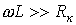 ), а емкостные проводимости конденсаторов много больше их активных проводимостей ( ), а емкостные проводимости конденсаторов много больше их активных проводимостей (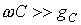 ).
Фильтрующие свойства четырехполюсников обусловлены возникающими в них резонансными режимами – резонансами токов и напряжений. Фильтры обычно собираются по симметричной Т- или П-образной схеме, т.е. при ).
Фильтрующие свойства четырехполюсников обусловлены возникающими в них резонансными режимами – резонансами токов и напряжений. Фильтры обычно собираются по симметричной Т- или П-образной схеме, т.е. при 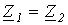 или или 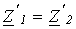 (см. лекцию №14). В этой связи при изучении фильтров будем использовать введенные в предыдущей лекции понятия коэффициентов затухания и фазы.
Классификация фильтров в зависимости от диапазона пропускаемых частот приведена в табл. 1.
Таблица 1. Классификация фильтров (см. лекцию №14). В этой связи при изучении фильтров будем использовать введенные в предыдущей лекции понятия коэффициентов затухания и фазы.
Классификация фильтров в зависимости от диапазона пропускаемых частот приведена в табл. 1.
Таблица 1. Классификация фильтров
В соответствии с материалом, изложенным в предыдущей лекции, если фильтр имеет нагрузку, сопротивление которой при всех частотах равно характеристическому, то напряжения и соответственно токи на его входе и выходе связаны соотношением
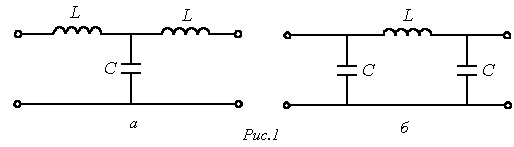
В идеальном случае в полосе пропускания (прозрачности) Рассмотрим схему простейшего низкочастотного фильтра,представленную на рис. 1,а.
Связь коэффициентов четырехполюсника с параметрами элементов Т-образной схемы замещения определяется соотношениями (см. лекцию № 14)
или конкретно для фильтра на рис. 1,а
Из уравнений четырехполюсника, записанных с использованием гиперболических функций (см. лекцию № 14), вытекает, что
Однако в соответствии с (2)
Поскольку в полосе пропускания частот коэффициент затухания
Так как пределы изменения
которому удовлетворяют частоты, лежащие в диапазоне
Для характеристического сопротивления фильтра на основании (3) и (4) имеем
Анализ соотношения (7) показывает, что с ростом частоты w в пределах, определяемых неравенством (6), характеристическое сопротивление фильтра уменьшается до нуля, оставаясь активным. Поскольку, при нагрузке фильтра сопротивлением, равным характеристическому, его входное сопротивление также будет равно
Следует отметить, что вне полосы пропускания
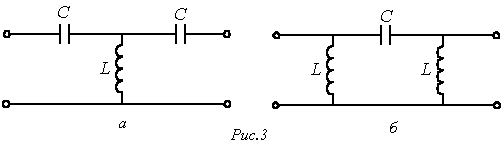
Так как вне полосы прозрачности В полосе задерживания коэффициент затухания Другим вариантом простейшего низкочастотного фильтра может служить четырехполюсник по схеме на рис. 1,б. Схема простейшего высокочастотного фильтра приведена на рис. 3,а.
Для данного фильтра коэффициенты четырехполюсника определяются выражениями
Как и для рассмотренного выше случая, А – вещественная переменная. Поэтому на основании (9)
Данному неравенству удовлетворяет диапазон изменения частот
Характеристическое сопротивление фильтра
Вне области пропускания частот
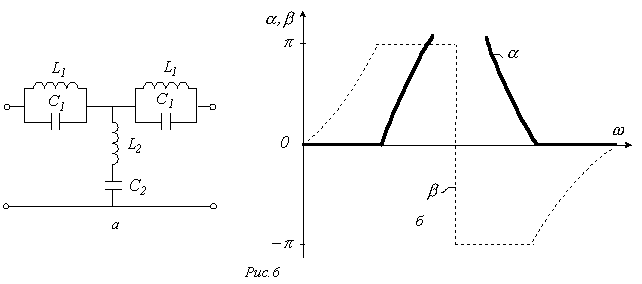
при Качественный вид зависимостей Следует отметить, что другим примером простейшего высокочастотного фильтра может служить П-образный четырехполюсник на рис. 3,б. Полосовой фильтр формально получается путем последовательного соединения низкочастотного фильтра с полосой пропускания
приведена на рис. 5,а, а на рис. 5,б представлены качественные зависимости У режекторного фильтра полоса прозрачности разделена на две части полосой затухания. Схема простейшего режекторного фильтра и качественные зависимости
В заключение необходимо отметить, что для улучшения характеристик фильтров всех типов их целесообразно выполнять в виде цепной схемы, представляющей собой каскадно включенные четырехполюсники. При обеспечении согласованного режима работы всех n звеньев схемы коэффициент затухания
Литература
Контрольные вопросы и задачи
Ответ: | |||||||||||||||||||||||||||||||||||||||||
| Лекция N 16. Трехфазные электрические цепи. |
Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Отметим, что обычно эти ЭДС, в первую очередь в силовой энергетике, синусоидальны. Однако, в современных электромеханических системах, где для управления исполнительными двигателями используются преобразователи частоты, система напряжений в общем случае является несинусоидальной. Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой,т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке.
Таким образом, понятие «фаза» имеет в электротехнике два различных значения:
 Источником трехфазного напряжения является трехфазный генератор, на статоре которого (см. рис. 1) размещена трехфазная обмотка. Фазы этой обмотки располагаются таким образом, чтобы их магнитные оси были сдвинуты в пространстве друг относительно друга на
Источником трехфазного напряжения является трехфазный генератор, на статоре которого (см. рис. 1) размещена трехфазная обмотка. Фазы этой обмотки располагаются таким образом, чтобы их магнитные оси были сдвинуты в пространстве друг относительно друга на  эл. рад. На рис. 1 каждая фаза статора условно показана в виде одного витка. Начала обмоток принято обозначать заглавными буквами А,В,С, а концы- соответственно прописными x,y,z. ЭДС в неподвижных обмотках статора индуцируются в результате пересечения их витков магнитным полем, создаваемым током обмотки возбуждения вращающегося ротора (на рис. 1 ротор условно изображен в виде постоянного магнита, что используется на практике при относительно небольших мощностях). При вращении ротора с равномерной скоростью в обмотках фаз статора индуцируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся вследствие пространственного сдвига друг от друга по фазе на эл. рад. На рис. 1 каждая фаза статора условно показана в виде одного витка. Начала обмоток принято обозначать заглавными буквами А,В,С, а концы- соответственно прописными x,y,z. ЭДС в неподвижных обмотках статора индуцируются в результате пересечения их витков магнитным полем, создаваемым током обмотки возбуждения вращающегося ротора (на рис. 1 ротор условно изображен в виде постоянного магнита, что используется на практике при относительно небольших мощностях). При вращении ротора с равномерной скоростью в обмотках фаз статора индуцируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся вследствие пространственного сдвига друг от друга по фазе на  рад. (см. рис. 2).
Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются:
- экономичность передачи электроэнергии на большие расстояния;
- самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором;
- возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств;
- уравновешенность симметричных трехфазных систем.
Для рассмотрения важнейшего свойства уравновешенноститрехфазной системы, которое будет доказано далее, введем понятие симметрии многофазной системы.
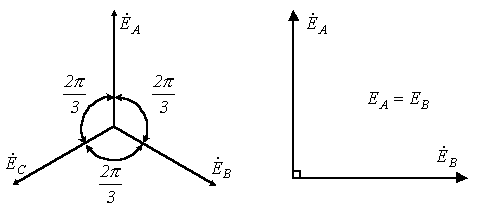
Система ЭДС (напряжений, токов и т.д.) называется симметричной,если она состоит из m одинаковых по модулю векторов ЭДС (напряжений, токов и т.д.), сдвинутых по фазе друг относительно друга на одинаковый угол рад. (см. рис. 2).
Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются:
- экономичность передачи электроэнергии на большие расстояния;
- самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором;
- возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств;
- уравновешенность симметричных трехфазных систем.
Для рассмотрения важнейшего свойства уравновешенноститрехфазной системы, которое будет доказано далее, введем понятие симметрии многофазной системы.
Система ЭДС (напряжений, токов и т.д.) называется симметричной,если она состоит из m одинаковых по модулю векторов ЭДС (напряжений, токов и т.д.), сдвинутых по фазе друг относительно друга на одинаковый угол 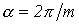 . В частности векторная диаграмма для симметричной системы ЭДС, соответствующей трехфазной системе синусоид на рис. 2, представлена на рис. 3. . В частности векторная диаграмма для симметричной системы ЭДС, соответствующей трехфазной системе синусоид на рис. 2, представлена на рис. 3.
Из несимметричных систем наибольший практический интерес представляет двухфазная система с 90-градусным сдвигом фаз (см. рис. 4). Все симметричные трех- и m-фазные (m>3) системы, а также двухфазная система являются уравновешенными. Это означает, что хотя в отдельных фазах мгновенная мощность пульсирует (см. рис. 5,а), изменяя за время одного периода не только величину, но в общем случае и знак, суммарная мгновенная мощность всех фаз остается величиной постоянной в течение всего периода синусоидальной ЭДС (см. рис. 5,б). Уравновешенность имеет важнейшее практическое значение. Если бы суммарная мгновенная мощность пульсировала, то на валу между турбиной и генератором действовал бы пульсирующий момент. Такая переменная механическая нагрузка вредно отражалась бы на энергогенерирующей установке, сокращая срок ее службы. Эти же соображения относятся и к многофазным электродвигателям.
Если симметрия нарушается (двухфазная система Тесла в силу своей специфики в расчет не принимается), то нарушается и уравновешенность. Поэтому в энергетике строго следят за тем, чтобы нагрузка генератора оставалась симметричной.
|

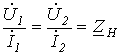 .
. и называют характеристическим сопротивлением симметричного четырехполюсника, а режим работы четырехполюсника, для которого справедливо
и называют характеристическим сопротивлением симметричного четырехполюсника, а режим работы четырехполюсника, для которого справедливо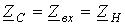 ,
, на основании (3) и (4) можно записать
на основании (3) и (4) можно записать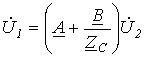 ;
;
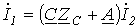 .
.
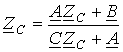 ,
,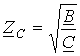 .
.
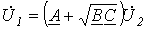 ;
;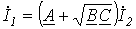 .
.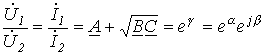 ,
,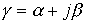 - коэффициент распространения;
- коэффициент распространения; 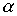 - коэффициент затухания (измеряется в неперах);
- коэффициент затухания (измеряется в неперах);  - коэффициент фазы (измеряется в радианах).
- коэффициент фазы (измеряется в радианах).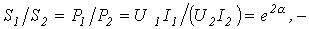 в е2 раз.
в е2 раз. .
.
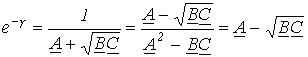 .
.
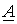 и
и 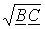 , получим
, получим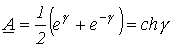 и
и  .
.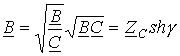
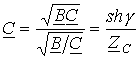 ,
,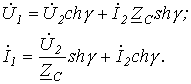
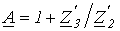 ;
; 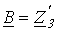 ;
; 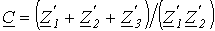 ;
; 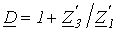 .
.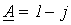 ;
;  ;
; 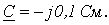
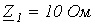 ;
; 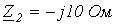 ;
; 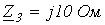 .
. ;
;  .
.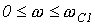
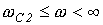
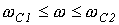
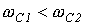
 .
.
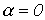 , т.е. в соответствии с (1)
, т.е. в соответствии с (1) 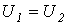 ,
, 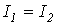 и
и  . Следовательно, справедливо и равенство
. Следовательно, справедливо и равенство 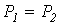 , которое указывает на отсутствие потерь в идеальном фильтре, а значит, идеальный фильтр должен быть реализован на основе идеальных катушек индуктивности и конденсаторов. Вне области пропускания (в полосе затухания) в идеальном случае
, которое указывает на отсутствие потерь в идеальном фильтре, а значит, идеальный фильтр должен быть реализован на основе идеальных катушек индуктивности и конденсаторов. Вне области пропускания (в полосе затухания) в идеальном случае  , т.е.
, т.е. 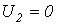 и
и 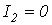 .
.
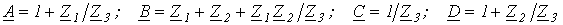
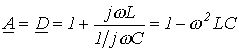 ;
;
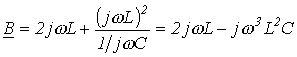 ;
;
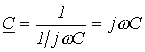 .
.
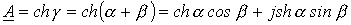 .
.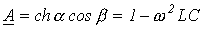 .
.
 .
.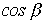 :
: 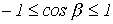 , - то границы полосы пропускания определяются неравенством
, - то границы полосы пропускания определяются неравенством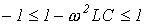 ,
,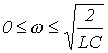 .
.
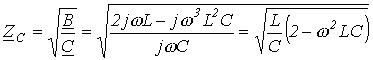 .
.
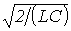 , как это следует из (7), характеристическое сопротивление приобретает индуктивный характер.
, как это следует из (7), характеристическое сопротивление приобретает индуктивный характер. На рис. 2 приведены качественные зависимости
На рис. 2 приведены качественные зависимости  и
и  .
.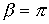 . Действительно, поскольку коэффициент А – вещественный, то всегда должно удовлетворяться равенство
. Действительно, поскольку коэффициент А – вещественный, то всегда должно удовлетворяться равенство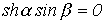 .
.
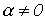 , то соотношение (8) может выполняться только при
, то соотношение (8) может выполняться только при 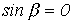 .
.
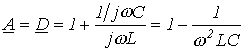 ;
;
 ;
;
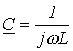 .
.
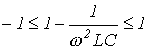 .
. .
.
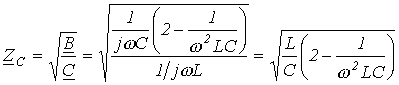 ,
,
 изменяясь в пределах от нуля до
изменяясь в пределах от нуля до 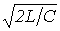 с ростом частоты, остается вещественным. Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с нагрузкой во всей полосе пропускания практически невозможно, реально фильтр работает с
с ростом частоты, остается вещественным. Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с нагрузкой во всей полосе пропускания практически невозможно, реально фильтр работает с 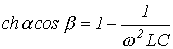
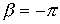 . Плавное изменение коэффициента затухания в соответствии с (14) показывает, что в полосе задерживания фильтр не является идеальным.
. Плавное изменение коэффициента затухания в соответствии с (14) показывает, что в полосе задерживания фильтр не является идеальным.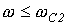 и высокочастотного с полосой пропускания
и высокочастотного с полосой пропускания 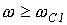 , причем
, причем  . Схема простейшего полосового фильтра
. Схема простейшего полосового фильтра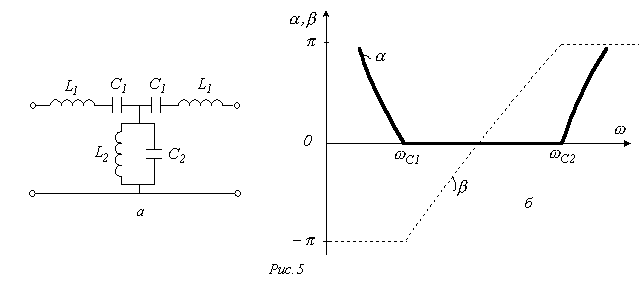
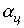 такого фильтра возрастает в соответствии с выражением
такого фильтра возрастает в соответствии с выражением 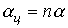 , что приближает фильтр к идеальному.
, что приближает фильтр к идеальному.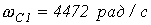 ,
,  .
.