Соединение в треугольник
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).
Для симметричной системы ЭДС имеем
Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рис. 8 токи будут равны нулю. Однако, если поменять местами начало и конец любой из фаз, то Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9. Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями
На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов
В заключение отметим, что помимо рассмотренных соединений «звезда - звезда» и «треугольник - треугольник» на практике также применяются схемы «звезда - треугольник» и «треугольник - звезда».
Литература
Контрольные вопросы и задачи
| |||
| Лекция N 17. Расчет трехфазных цепей. |
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в символической форме в полной мере распространяются на них. Анализ трехфазных систем удобно осуществлять с использованием векторных диаграмм, позволяющих достаточно просто определять фазовые сдвиги между переменными. Однако определенная специфика многофазных цепей вносит характерные особенности в их расчет, что, в первую очередь, касается анализа их работы в симметричных режимах.
Расчет симметричных режимов работы трехфазных систем
Многофазный приемник и вообще многофазная цепь называются симметричными,если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. если  . В противном случае они являются несимметричными.Равенство модулей указанных сопротивлений не является достаточным условием симметрии цепи. Так, например трехфазный приемник на рис. 1,а является симметричным, а на рис. 1,б – нет даже при условии: . В противном случае они являются несимметричными.Равенство модулей указанных сопротивлений не является достаточным условием симметрии цепи. Так, например трехфазный приемник на рис. 1,а является симметричным, а на рис. 1,б – нет даже при условии:  . .
 Если к симметричной трехфазной цепи приложена симметричная трехфазная система напряжений генератора, то в ней будет иметь место симметричная система токов. Такой режим работы трехфазной цепи называется симметричным.В этом режиме токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг по отношению к другу на угол
Если к симметричной трехфазной цепи приложена симметричная трехфазная система напряжений генератора, то в ней будет иметь место симметричная система токов. Такой режим работы трехфазной цепи называется симметричным.В этом режиме токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг по отношению к другу на угол 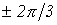 . Вследствие указанного расчет таких цепей проводится для одной – базовой – фазы, в качестве которой обычно принимают фазу А. При этом соответствующие величины в других фазах получают формальным добавлением к аргументу переменной фазы А фазового сдвига . Вследствие указанного расчет таких цепей проводится для одной – базовой – фазы, в качестве которой обычно принимают фазу А. При этом соответствующие величины в других фазах получают формальным добавлением к аргументу переменной фазы А фазового сдвига 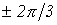 при сохранении неизменным ее модуля.
Так для симметричного режима работы цепи на рис. 2,а при известных линейном напряжении и сопротивлениях фаз при сохранении неизменным ее модуля.
Так для симметричного режима работы цепи на рис. 2,а при известных линейном напряжении и сопротивлениях фаз  можно записать можно записать
 ,
где ,
где  определяется характером нагрузки определяется характером нагрузки  .
Тогда на основании вышесказанного .
Тогда на основании вышесказанного
 ; ;
 . .
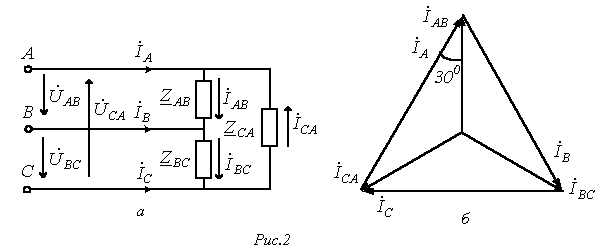 Комплексы линейных токов можно найти с использованием векторной диаграммы на рис. 2,б, из которой вытекает:
Комплексы линейных токов можно найти с использованием векторной диаграммы на рис. 2,б, из которой вытекает:
 При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется с помощью двух основных приемов:
Все треугольники заменяются эквивалентными звездами. Поскольку треугольники симметричны, то в соответствии с формулами преобразования «треугольник-звезда»
При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется с помощью двух основных приемов:
Все треугольники заменяются эквивалентными звездами. Поскольку треугольники симметричны, то в соответствии с формулами преобразования «треугольник-звезда»  .
Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам которого определяются соответствующие величины в других фазах.
Пусть, например, при заданном фазном напряжении .
Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам которого определяются соответствующие величины в других фазах.
Пусть, например, при заданном фазном напряжении  необходимо определить линейные токи необходимо определить линейные токи 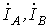 и и 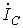 в схеме на рис. 3, все сопротивления в которой известны.
В соответствии с указанной методикой выделим расчетную фазу А, которая представлена на рис. 4. Здесь в схеме на рис. 3, все сопротивления в которой известны.
В соответствии с указанной методикой выделим расчетную фазу А, которая представлена на рис. 4. Здесь  , ,  .
Тогда для тока .
Тогда для тока  можно записать можно записать
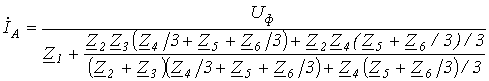 ,
и соответственно ,
и соответственно 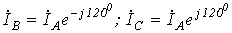 . .

 Расчет несимметричных режимов работы трехфазных систем
Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет место несимметричный режим работы. Такие режимы при наличии в цепи только статической нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить, что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес также потенциалы узлов, чаще других для расчета сложных схем применяется метод узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей с электрическими машинами в основном применяется метод симметричных составляющих, который будет рассмотрен далее.
При заданных линейных напряжениях наиболее просто рассчитываются трехфазные цепи при соединении в треугольник. Пусть в схеме на рис. 2,а
Расчет несимметричных режимов работы трехфазных систем
Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет место несимметричный режим работы. Такие режимы при наличии в цепи только статической нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить, что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес также потенциалы узлов, чаще других для расчета сложных схем применяется метод узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей с электрическими машинами в основном применяется метод симметричных составляющих, который будет рассмотрен далее.
При заданных линейных напряжениях наиболее просто рассчитываются трехфазные цепи при соединении в треугольник. Пусть в схеме на рис. 2,а  . Тогда при известных комплексах линейных напряжений в соответствии с законом Ома . Тогда при известных комплексах линейных напряжений в соответствии с законом Ома
 ; ;  ; ;  .
По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи: .
По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи:
 .
Обычно на практике известны не комплексы линейных напряжений, а их модули. В этом случае необходимо предварительное определение начальных фаз этих напряжений, что можно осуществить, например, графически. Для этого, приняв .
Обычно на практике известны не комплексы линейных напряжений, а их модули. В этом случае необходимо предварительное определение начальных фаз этих напряжений, что можно осуществить, например, графически. Для этого, приняв 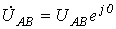 , по заданным модулям напряжений, строим треугольник (см. рис.5), из которого (путем замера) определяем значения углов a и b. , по заданным модулям напряжений, строим треугольник (см. рис.5), из которого (путем замера) определяем значения углов a и b.
 Тогда Тогда
 Искомые углы a и b могут быть также найдены аналитически на основании теоремы косинусов:
Искомые углы a и b могут быть также найдены аналитически на основании теоремы косинусов:
 При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям на фазах источника. В этом случае фазные токи легко определяются по закону Ома, т.е. путем деления известных напряжений на фазах потребителя на соответствующие сопротивления. Однако, если сопротивление нейтрального провода велико или он отсутствует, требуется более сложный расчет.
Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной нагрузке
При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям на фазах источника. В этом случае фазные токи легко определяются по закону Ома, т.е. путем деления известных напряжений на фазах потребителя на соответствующие сопротивления. Однако, если сопротивление нейтрального провода велико или он отсутствует, требуется более сложный расчет.
Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной нагрузке  ей в общем случае будет соответствовать векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки источника и приемника занимают разные положения, т.е. ей в общем случае будет соответствовать векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки источника и приемника занимают разные положения, т.е.  .
Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением смещения нейтральной точки(обычно принимается, что .
Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением смещения нейтральной точки(обычно принимается, что  ) или просто напряжением смещения нейтрали.Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке, что наглядно иллюстрирует векторная диаграмма на рис. 6,б.
Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали. Если оно известно, то напряжения на фазах нагрузки равны: ) или просто напряжением смещения нейтрали.Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке, что наглядно иллюстрирует векторная диаграмма на рис. 6,б.
Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали. Если оно известно, то напряжения на фазах нагрузки равны:
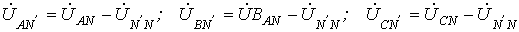 . .
 Тогда для искомых токов можно записать:
Тогда для искомых токов можно записать:
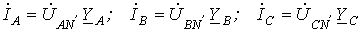 .
Соотношение для напряжения смещения нейтрали, записанное на основании метода узловых потенциалов, имеет вид .
Соотношение для напряжения смещения нейтрали, записанное на основании метода узловых потенциалов, имеет вид
При наличии нейтрального провода с нулевым сопротивлением
Запишем выражения комплексных сопротивлений фаз нагрузки:
Тогда для напряжения смещения нейтрали будем иметь
Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника опускается)
Таким образом, наиболее ярко будет гореть лампочка в фазе С. В заключение отметим, что если при соединении в звезду задаются линейные напряжения (что обычно имеет место на практике), то с учетом того, что сумма последних равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например,
Литература
Контрольные вопросы и задачи
Определить ток в нейтральном проводе. Ответ:
Определить ток в нейтральном проводе. Ответ:
Определить фазные напряжения на нагрузке. Ответ:
Определить фазные напряжения на нагрузке. Ответ: | ||||
| Лекция N 18. Применение векторных диаграмм для анализа несимметричных режимов. |
Несимметричные режимы в простейших характерных случаях (короткое замыкание и холостой ход) могут быть проанализированы на основе построения векторных диаграмм.
Рассмотрим режимы обрыва и короткого замыкания фазы при соединении в звезду для трех- и четырехпроводной систем. При этом будем проводить сопоставление с симметричным режимом работы цепи, фазные напряжения и токи в которой будут базовыми. Для этой цепи (см. рис.1,а) векторная диаграмма токов и напряжений приведена на рис. 1,б (принято, что нагрузка 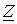 носит активно-индуктивный характер). Здесь носит активно-индуктивный характер). Здесь

 .
При обрыве фазы А нагрузки приходим к векторной диаграмме на рис. 2.
В этом случае .
При обрыве фазы А нагрузки приходим к векторной диаграмме на рис. 2.
В этом случае
 .
При коротком замыкании фазы А (трехпроводная система) имеет место векторная диаграмма на рис. 3. Из нее вытекает: .
При коротком замыкании фазы А (трехпроводная система) имеет место векторная диаграмма на рис. 3. Из нее вытекает:  ; ;  ; ;  ; ;  ; ;  .
При обрыве фазы А в четырехпроводной системе (нейтральный провод на рис. 1,а показан пунктиром, а вектор тока .
При обрыве фазы А в четырехпроводной системе (нейтральный провод на рис. 1,а показан пунктиром, а вектор тока  - пунктиром на рис. 1,б) - пунктиром на рис. 1,б) 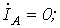  ; ;  ; ; 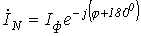 .
Симметричный трехфазный приемник при соединении в треугольник и соответствующая этому случаю векторная диаграмма напряжений и токов приведены на рис. 4. .
Симметричный трехфазный приемник при соединении в треугольник и соответствующая этому случаю векторная диаграмма напряжений и токов приведены на рис. 4.

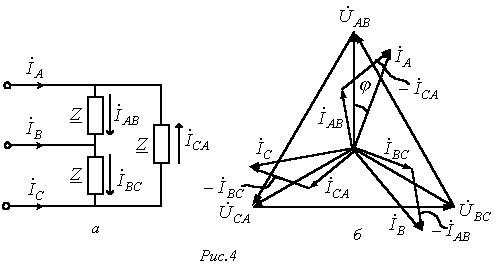 Здесь при том же способе соединения фаз генератора
Здесь при том же способе соединения фаз генератора  ; ;  ; ;  ; ;  ; ;  ; ;  . .
 При обрыве провода в фазе А-В нагрузки, как это видно из схемы на рис. 5, При обрыве провода в фазе А-В нагрузки, как это видно из схемы на рис. 5,  ; ;  , при этом сами токи , при этом сами токи  и и  в силу автономности режима работы фаз при соединении нагрузки в треугольник такие же, как и в цепи на рис. 4,а. Таким образом, в силу автономности режима работы фаз при соединении нагрузки в треугольник такие же, как и в цепи на рис. 4,а. Таким образом, 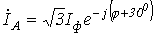 ; ;  ; ;  .
Цепь при обрыве линейного провода А-А’ и соответствующая этому случаю векторная диаграмма приведены на рис.6. .
Цепь при обрыве линейного провода А-А’ и соответствующая этому случаю векторная диаграмма приведены на рис.6.
 Здесь
Здесь
 ; ;  ; ;  .
Мощность в трехфазных цепях
Мгновенная мощность трехфазного источника энергии равна сумме мгновенных мощностей его фаз: .
Мощность в трехфазных цепях
Мгновенная мощность трехфазного источника энергии равна сумме мгновенных мощностей его фаз:
 .
Активная мощность генератора, определяемая как среднее за период значение мгновенной мощности, равна .
Активная мощность генератора, определяемая как среднее за период значение мгновенной мощности, равна
 .
Соответственно активная мощность трехфазного приемника с учетом потерь в сопротивлении нейтрального провода .
Соответственно активная мощность трехфазного приемника с учетом потерь в сопротивлении нейтрального провода
 ,
реактивная ,
реактивная
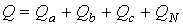 и полная
и полная
 .
Суммарная активная мощность симметричной трехфазной системы .
Суммарная активная мощность симметричной трехфазной системы
Учитывая, что в симметричном режиме для звезды имеют место соотношения
и для треугольника -
на основании (1) для обоих способов соединения фаз получаем
где j - угол сдвига между фазными напряжением и током. Аналогично
Докажем теперь указанное ранее свойство уравновешенности двухфазной системы Тесла и симметричной трехфазной системы.
1. Двухфазная система Тесла
С учетом (2) и (3)
Таким образом, суммарная мгновенная мощность фаз есть величина постоянная, равная суммарной активной мощности источника.
2. Симметричная трехфазная цепь
Тогда
Отсюда
т.е. и для симметричной трехфазной цепи свойство уравновешенности доказано.
|


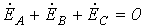 .
. и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой.
и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой.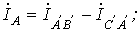

 Аналогично можно выразить линейные токи через фазные токи генератора.
Аналогично можно выразить линейные токи через фазные токи генератора. .
.
 . Определить комплексы остальных фазных и линейных токов.
. Определить комплексы остальных фазных и линейных токов.  .
.
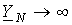 , и из (1)
, и из (1)  . В случае отсутствия нейтрального провода
. В случае отсутствия нейтрального провода  . При симметричной нагрузке
. При симметричной нагрузке  с учетом того, что
с учетом того, что 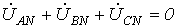 , из (1) вытекает
, из (1) вытекает  В качестве примера анализа несимметричного режима работы цепи с использованием соотношения (1) определим, какая из ламп в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если
В качестве примера анализа несимметричного режима работы цепи с использованием соотношения (1) определим, какая из ламп в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если 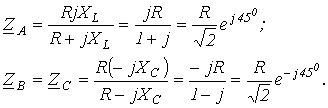


 и
и  . Тогда, поскольку при этом
. Тогда, поскольку при этом  , соотношение (1) трансформируется в формулу
, соотношение (1) трансформируется в формулу .
.
 ;
;  ;
;  ;
;  . Линейное напряжение равно 380 В.
. Линейное напряжение равно 380 В.  .
. ;
;  . Остальные параметры те же.
. Остальные параметры те же.  .
. ;
;  ;
; 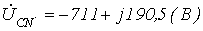 .
. ;
;  ;
;  .
.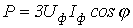 .
.


 ,
,
 В соответствии с рис. 7
В соответствии с рис. 7
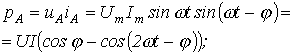
 .
.
 .
.

 ,
,


