Применение метода симметричных составляющих для симметричных цепей
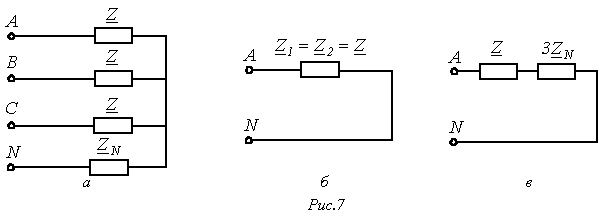
Расчет цепей методом симметричных составляющих основывается на принципе наложения, в виду чего метод применим только к линейным цепям. Согласно данному методу расчет осуществляется в отдельности для составляющих напряжений и токов различных последовательностей, причем в силу симметрии режимов работы цепи для них он проводится для одной фазы (фазы А). После этого в соответствии с (1)…(3) определяются реальные искомые величины. При расчете следует помнить, что, поскольку в симметричном режиме ток в нейтральном проводе равен нулю, сопротивление нейтрального провода никак ни влияет на симметричные составляющие токов прямой и обратной последовательностей. Наоборот, в схему замещения для нулевой последовательности на основании (7) вводится утроенное значение сопротивления в нейтральном проводе. С учетом вышесказанного исходной схеме на рис. 7,а соответствуют расчетные однофазные цепи для прямой и обратной последовательностей (рис. 7,б) и нулевой последовательности (рис. 7,в).
Существенно сложнее обстоит дело при несимметрии сопротивлений по фазам. Пусть в цепи на рис. 3
В свою очередь
Подставив в (11) значения соответствующих параметров из (10) после группировки членов получим
где
Из полученных соотношений видно, что если к несимметричной цепи приложена несимметричная система напряжений, то каждая из симметричных составляющих токов зависит от симметричных составляющих напряжений всех последовательностей. Поэтому, если бы трехфазная цепь на всех участках была несимметрична, рассматриваемый метод расчета не давал бы преимуществ. На практике система в основном является симметричной, а несимметрия обычно носит локальный характер. Это обстоятельство, как будет показано в следующей лекции, значительно упрощает анализ. На всех участках цепи, где сопротивления по фазам одинаковы,
Литература
Контрольные вопросы и задачи
Ответ:
Ответ:
Ответ: | |||||||
| Лекция N 20. Теорема об активном двухполюснике для симметричных составляющих. |
В тех случаях, когда трехфазная цепь в целом симметрична, а несимметрия носит локальный характер (местное короткое замыкание или обрыв фазы, подключение несимметричной нагрузки), для расчета удобно применять теорему об активном двухполюснике.
При мысленном устранении несимметрии (несимметричного участка) для оставшейся цепи имеет место симметричный режим холостого хода. В соответствии с методом эквивалентного генератора теперь необходимо определить эквивалентные ЭДС и входные сопротивления симметричной цепи. В общем случае – при несимметрии в системе фазных напряжений источника – помимо эквивалентной ЭДС прямой последовательности  будут также иметь место эквивалентные ЭДС обратной будут также иметь место эквивалентные ЭДС обратной  и нулевой и нулевой  последовательностей. Однако обычно напряжения генераторов симметричны – тогда последовательностей. Однако обычно напряжения генераторов симметричны – тогда  . Величина . Величина  , соответствующая напряжению холостого хода , соответствующая напряжению холостого хода  на зажимах подключения локальной несимметрии, определяется при отключении локальной несимметричной нагрузки любым известным методом расчета линейных цепей, причем в силу симметрии цепи расчет проводится для одной фазы.
В отдельности рассчитываются входные сопротивления симметричной цепи для различных последовательностей, которая предварительно преобразуется известными методами в пассивную цепь. При этом при расчете входного сопротивления нулевой последовательности на зажимах подключения локальной несимметрии, определяется при отключении локальной несимметричной нагрузки любым известным методом расчета линейных цепей, причем в силу симметрии цепи расчет проводится для одной фазы.
В отдельности рассчитываются входные сопротивления симметричной цепи для различных последовательностей, которая предварительно преобразуется известными методами в пассивную цепь. При этом при расчете входного сопротивления нулевой последовательности  необходимо учитывать только те участки цепи, которые соединены с нейтральным проводом или заземленной нейтральной точкой, т.е. принимать во внимание только те ветви, по которым могут протекать токи нулевой последовательности. Схемы для расчета входных сопротивлений прямой и обратной последовательностей одинаковы, однако в случае вращающихся машин величины этих сопротивлений различны.
Поскольку в отдельности для каждой симметричной последовательности имеет место симметричный режим, расчет указанным методом ведется на одну фазу с использованием расчетных схем для прямой (рис. 1,а), обратной (рис. 1,б) и нулевой (рис. 1,в) последовательностей. необходимо учитывать только те участки цепи, которые соединены с нейтральным проводом или заземленной нейтральной точкой, т.е. принимать во внимание только те ветви, по которым могут протекать токи нулевой последовательности. Схемы для расчета входных сопротивлений прямой и обратной последовательностей одинаковы, однако в случае вращающихся машин величины этих сопротивлений различны.
Поскольку в отдельности для каждой симметричной последовательности имеет место симметричный режим, расчет указанным методом ведется на одну фазу с использованием расчетных схем для прямой (рис. 1,а), обратной (рис. 1,б) и нулевой (рис. 1,в) последовательностей.
 Данным схемам соответствуют соотношения
Данным схемам соответствуют соотношения
Поскольку соотношений три, а число входящих в них неизвестных шесть Рассмотрим некоторые типовые примеры применения метода. Однополюсное короткое замыкание на землю (рис. 2).
Поскольку фаза А замкнута на землю, то дополнительные уравнения имеют вид
Тогда
С учетом последних соотношений уравнения (1)…(3) можно записать в виде
Принимая во внимание (4), а также то, что источник питания симметричный
откуда получаем
Двухполюсное короткое замыкание без земли (рис. 3). Для рассматриваемого случая можно записать
Последнее равенство объясняется отсутствием пути для протекания токов нулевой последовательности.
Из двух последних соотношений вытекает, что Подставив полученные выражения для напряжений и токов прямой и обратной последовательностей в (1) и (2), запишем
Вычитая из (8) соотношение (9) и учитывая, что в силу симметрии источника
откуда
Обрыв линейного провода (рис. 4) – определить напряжение в месте разрыва.
Из соотношений (11) и (12) вытекает равенство:
На основании (1)…(3) с учетом (13) запишем
Принимая во внимание симметричность источника
- откуда
Таким образом, искомое напряжение
Учитывая, что
Решая данную систему уравнений, находим
и В рассмотренных примерах предполагалось, что необходимые для анализа цепи параметры
Поскольку при отключении несимметричной нагрузки
Схема для определения входных сопротивлений прямой
Схема для определения
|

 . Разложив токи на симметричные составляющие, для данной цепи можно записать
. Разложив токи на симметричные составляющие, для данной цепи можно записать


 ;
;
 для i¹k. Тогда из (12) получаем
для i¹k. Тогда из (12) получаем .
. , если
, если  ,
,  .
.  .
. .
.  ;
;  .
. и
и  . Определить действующие значения токов в фазах двигателя, если его сопротивления прямой и обратной последовательностей соответственно равны:
. Определить действующие значения токов в фазах двигателя, если его сопротивления прямой и обратной последовательностей соответственно равны:  ;
; 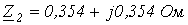 . Нейтральный провод отсутствует.
. Нейтральный провод отсутствует.  ;
;  ;
;  .
. ;
;
 ;
;
 .
.
 , необходимо составление трех дополнительных уравнений, учитывающих конкретный вид несимметрии.
, необходимо составление трех дополнительных уравнений, учитывающих конкретный вид несимметрии.
 .
. ;
;
 ;
; .
.
 ;
;
 ;
;
 .
.
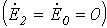 , просуммируем (5), (6) и (7):
, просуммируем (5), (6) и (7): ,
,



 . При этом
. При этом  , так как
, так как 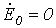 и
и  .
.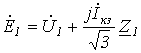 ;
;
 .
.
 , получим
, получим ,
, .
. В рассматриваемом случае дополнительные уравнения имеют вид
В рассматриваемом случае дополнительные уравнения имеют вид ;
;
 ;
;
 .
.
 .
.
 .
. ,
, .
. .
. Подключение несимметричной нагрузки
Подключение несимметричной нагрузки  к симметричной цепи (рис. 5).
к симметричной цепи (рис. 5). , подставим в уравнения (1)…(3) определенные в предыдущей лекции выражения
, подставим в уравнения (1)…(3) определенные в предыдущей лекции выражения  и
и  (см. соотношение (12) в лекции №19):
(см. соотношение (12) в лекции №19):
 и
и  . Тогда
. Тогда
 .
. и
и 
 оставшаяся часть схемы будет работать в симметричном режиме, для определения
оставшаяся часть схемы будет работать в симметричном режиме, для определения  Из нее
Из нее .
. и обратной
и обратной  последовательностей одна и та же и соответствует цепи на рис. 8,а. В соответствии с ней
последовательностей одна и та же и соответствует цепи на рис. 8,а. В соответствии с ней
 .
. .
.


