Измерение мощности в трехфазных цепях
Ниже рассмотрены практические схемы включения ваттметров для измерения мощности в трехфазных цепях. 1. Четырехпроводная система, несимметричный режим. Представленная на рис. 8 схема называется схемой трех ваттметров.
2. Четырехпроводная система, симметричный режим. Если режим работы цепи симметричный, то для определения суммарной активной мощности достаточно ограничиться одним ваттметром (любым), включаемым по схеме на рис. 8. Тогда, например, при включении прибора в фазу А,
3. Трехпроводная система, симметричный режим.
4. Трехпроводная система, симметричный режим; измерение реактивной мощности. С помощью одного ваттметра при симметричном режиме работы цепи можно измерить ее реактивную мощность. В этом случае схема включения ваттметра будет иметь вид по рис. 10,а. Согласно векторной диаграмме на рис. 10,б измеряемая прибором мощность
Таким образом, суммарная реактивная мощность
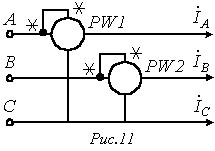
5. Трехпроводная система, несимметричный режим. Представленная на рис. 11 схема называется схемой двух ваттметров. В ней сумма показаний приборов равна суммарной активной мощности цепи.
Действительно, показания приборов в данной схеме:
Тогда
В заключение отметим, что если в схеме на рис. 11 имеет место симметричный режим работы, то на основании показаний приборов можно определить суммарную реактивную мощность цепи
Литература
Контрольные вопросы и задачи
Ответ:
Ответ: в два раза.
Ответ:
Определить показание ваттметра. Ответ:
Определить показания ваттметров. Ответ:
| |||||
| Лекция N 19. Метод симметричных составляющих. |
Метод симметричных составляющих относится к специальным методам расчета трехфазных цепей и широко применяется для анализа несимметричных режимов их работы, в том числе с нестатической нагрузкой. В основе метода лежит представление несимметричной трехфазной системы переменных (ЭДС, токов, напряжений и т.п.) в виде суммы трех симметричных систем, которые называют симметричными составляющими.Различают симметричные составляющие прямой, обратнойи нулевойпоследовательностей, которые различаются порядком чередования фаз.
Симметричную систему прямой последовательности образуют (см. рис. 1,а) три одинаковых по модулю вектора 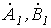 и и 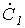 со сдвигом друг по отношению к другу на со сдвигом друг по отношению к другу на  рад., причем рад., причем 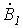 отстает от отстает от  , а , а 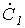 - от - от 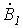 . .
 Введя, оператор поворота
Введя, оператор поворота  , для симметричной системы прямой последовательности можно записать , для симметричной системы прямой последовательности можно записать
 .
Симметричная система обратной последовательности образована равными по модулю векторами .
Симметричная система обратной последовательности образована равными по модулю векторами  и и  с относительным сдвигом по фазе на с относительным сдвигом по фазе на  рад., причем теперь рад., причем теперь  отстает от отстает от 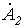 , а , а 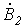 - от - от  (см. рис. 1,б). Для этой системы имеем (см. рис. 1,б). Для этой системы имеем
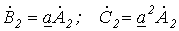 . .
 Система нулевой последовательности состоит из трех векторов, одинаковых по модулю и фазе (см. рис. 1,в): Система нулевой последовательности состоит из трех векторов, одинаковых по модулю и фазе (см. рис. 1,в):
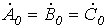 .
При сложении трех указанных систем векторов получается несимметричная система векторов (см. рис. 2).
Любая несимметричная система однозначно раскладывается на симметричные составляющие. Действительно, .
При сложении трех указанных систем векторов получается несимметричная система векторов (см. рис. 2).
Любая несимметричная система однозначно раскладывается на симметричные составляющие. Действительно,
Таким образом, получена система из трех уравнений относительно трех неизвестных
Для нахождения
Для определения
Формулы (1)…(6) справедливы для любой системы векторов В заключение раздела отметим, что помимо вычисления симметричные составляющие могут быть измерены с помощью специальных фильтров симметричных составляющих, используемых в устройствах релейной защиты и автоматики.
|

 Суммарная активная мощность цепи определяется как сумма показаний трех ваттметров
Суммарная активная мощность цепи определяется как сумма показаний трех ваттметров .
.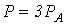 .
.
 При отсутствии доступа к нейтральной точке последняя создается искусственно с помощью включения трех дополнительных резисторов по схеме «звезда», как показано на рис. 9 – схема ваттметра с искусственной нейтральной точкой. При этом необходимо выполнение условия
При отсутствии доступа к нейтральной точке последняя создается искусственно с помощью включения трех дополнительных резисторов по схеме «звезда», как показано на рис. 9 – схема ваттметра с искусственной нейтральной точкой. При этом необходимо выполнение условия 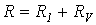 , где
, где  - собственное сопротивление обмотки ваттметра. Тогда суммарная активная мощность трехфазной системы определяется согласно (4).
- собственное сопротивление обмотки ваттметра. Тогда суммарная активная мощность трехфазной системы определяется согласно (4).
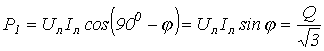 .
.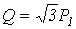 .
.
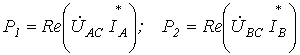 .
.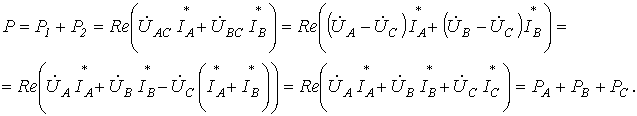
 .
.
 .
.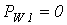 .
.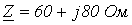 соединена в звезду. Линейное напряжение
соединена в звезду. Линейное напряжение 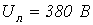 .
.  .
. .
. ;
;
 ;
;
 .
.
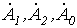 , которые, следовательно, определяются однозначно. Для нахождения
, которые, следовательно, определяются однозначно. Для нахождения 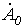 сложим уравнения (1)…(3). Тогда, учитывая, что
сложим уравнения (1)…(3). Тогда, учитывая, что 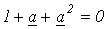 , получим
, получим .
.
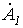 умножим (2) на
умножим (2) на 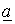 , а (3) – на
, а (3) – на 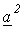 , после чего полученные выражения сложим с (1). В результате приходим к соотношению
, после чего полученные выражения сложим с (1). В результате приходим к соотношению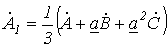 .
.
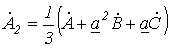 .
.
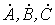 , в том числе и для симметричной. В последнем случае
, в том числе и для симметричной. В последнем случае 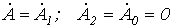 .
.


