Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть  , а
, а  . Тогда комплекс полной мощности:
. Тогда комплекс полной мощности:
 , ,
| (9)
|
где  - комплекс, сопряженный с комплексом
- комплекс, сопряженный с комплексом  .
.
 .
.
 Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует
Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует  (активно-индуктивная нагрузка), для которого имеем:
(активно-индуктивная нагрузка), для которого имеем:
.
Применение статических конденсаторов для повышения cos 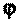
Как уже указывалось, реактивная мощность  циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению
циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению  в силовых электрических цепях.
в силовых электрических цепях.
Следует указать, что подавляющее большинство потребителей (электродвигатели, электрические печи, другие различные устройства и приборы) как нагрузка носит активно-индуктивный характер.
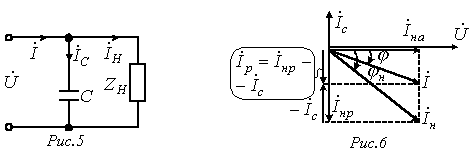
Если параллельно такой нагрузке 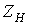 (см. рис. 5), включить конденсатор С, то общий ток
(см. рис. 5), включить конденсатор С, то общий ток  , как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е.
, как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е.  увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности
увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности  . На этом основано применение конденсаторов для повышения
. На этом основано применение конденсаторов для повышения  .
.
Какую емкость С нужно взять, чтобы повысить коэффициент мощности от значения  до значения
до значения  ?
?
Разложим  на активную
на активную  и реактивную
и реактивную  составляющие. Ток через конденсатор
составляющие. Ток через конденсатор 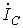 компенсирует часть реактивной составляющей тока нагрузки
компенсирует часть реактивной составляющей тока нагрузки  :
:
 ; ;
| (10)
|
 ; ;
| (11)
|
 . .
| (12)
|
Из (11) и (12) с учетом (10) имеем
 ,
,
но  , откуда необходимая для повышения
, откуда необходимая для повышения  емкость:
емкость:
 . .
| (13)
|

 , а
, а  . Тогда комплекс полной мощности:
. Тогда комплекс полной мощности: ,
,
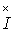 - комплекс, сопряженный с комплексом
- комплекс, сопряженный с комплексом  .
. .
. Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует
Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует  (активно-индуктивная нагрузка), для которого имеем:
(активно-индуктивная нагрузка), для которого имеем:
 циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению
циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению  в силовых электрических цепях.
в силовых электрических цепях.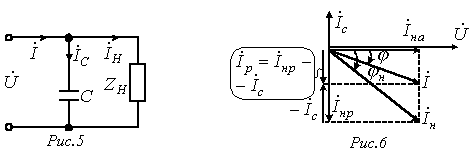
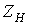 (см. рис. 5), включить конденсатор С, то общий ток
(см. рис. 5), включить конденсатор С, то общий ток  . На этом основано применение конденсаторов для повышения
. На этом основано применение конденсаторов для повышения  до значения
до значения  ?
? на активную
на активную  и реактивную
и реактивную  составляющие. Ток через конденсатор
составляющие. Ток через конденсатор 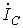 компенсирует часть реактивной составляющей тока нагрузки
компенсирует часть реактивной составляющей тока нагрузки  ;
;
 ;
;
 .
.
 ,
, , откуда необходимая для повышения
, откуда необходимая для повышения  .
.



