Метод узловых потенциалов
Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно Пусть имеем схему по рис. 4, в которой примем
Запишем уравнение по первому закону Кирхгофа для узла а: и подставим значения входящих в него токов, определенных выше: Сгруппировав соответствующие члены, получим: Аналогично можно записать для узла b: Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами: 1. В левой части i- гоуравнения записывается со знаком “+”потенциал Из сказанного следует, что все члены 2. В правой части i- гоуравнения записывается так называемый узловой ток В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью.
Литература
1. Основы теории цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. 2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с . Контрольные вопросы и задачи
1. В ветви на рис. 1 Ответ: 2. В чем заключается сущность символического метода расчета цепей синусоидального тока? 3. В чем состоит сущность метода контурных токов? 4. В чем состоит сущность метода узловых потенциалов? 5. В цепи на рис. 5 Ответ: 6. В цепи на рис. 6 Ответ:
| |
| Лекция N 6. Основы матричных методов расчета электрических цепей. |
Рассмотренные методы расчета электрических цепей – непосредственно по законам Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально рассчитать любую схему. Однако их применение без использования введенных ранее топологических матриц рационально для относительно простых схем. Использование матричных методов расчета позволяет формализовать процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем.
 Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
Пусть имеем схему по рис. 1, где Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
Пусть имеем схему по рис. 1, где  - источник тока. В соответствии с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы можно записать: - источник тока. В соответствии с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы можно записать:
Однако, для дальнейших выкладок будет удобнеепредставить ток
Подставив (2) в (1), получим:
Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви). Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства или
где Z – диагональная квадратная (размерностью n x n) матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю. Соотношение (4) представляет собой матричную запись закона Ома. Если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, согласно которому
то
то есть получили новую запись в матричной форме второго закона Кирхгофа.
|

 , т.е. числу ветвей дерева
, т.е. числу ветвей дерева  .
.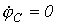 .
. Допустим, что
Допустим, что  и
и  известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС
известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС
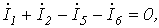
 .
. .
. .
.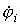 i- го узла, для которого составляется данное i- е уравнение, умноженный на сумму проводимостей
i- го узла, для которого составляется данное i- е уравнение, умноженный на сумму проводимостей 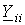 ветвей, присоединенных к данному i- му узлу, и со знаком “-”потенциал
ветвей, присоединенных к данному i- му узлу, и со знаком “-”потенциал  соседних узлов, каждый из которых умножен на сумму проводимостей
соседних узлов, каждый из которых умножен на сумму проводимостей  ветвей, присоединенных к i- му и k- му узлам.
ветвей, присоединенных к i- му и k- му узлам. , стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем
, стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем  . Последнее равенство по аналогии с методом контурных токов обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.
. Последнее равенство по аналогии с методом контурных токов обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.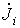 , равный сумме произведений ЭДС ветвей, подходящих к i- му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i- му узлу, в противном случае ставится знак “-”. Если в подходящих к i- му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.
, равный сумме произведений ЭДС ветвей, подходящих к i- му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i- му узлу, в противном случае ставится знак “-”. Если в подходящих к i- му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.

 . Определить ток
. Определить ток  .
. .
. ;
;  ;
; 
 ;
; 


 . Методом контурных токов определить комплексы действующих значений токов ветвей.
. Методом контурных токов определить комплексы действующих значений токов ветвей. ;
; 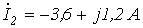 ;
;  .
.








 . Рассчитать токи в ветвях, используя метод узловых потенциалов.
. Рассчитать токи в ветвях, используя метод узловых потенциалов. ;
;  ;
;  ;
; 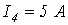 ;
;  ;
;  ;
;  .
.
 .
.
 как сумму токов k -й ветви и источника тока, т.е.:
как сумму токов k -й ветви и источника тока, т.е.: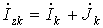 .
.
 .
.
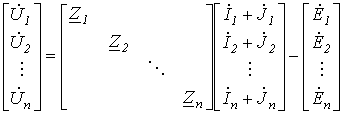
 ,
,
 ,
,
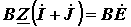 ,
,



