Практическое занятие. Кривые 2-го порядка: окружность, эллипс, гипербола.
^ Получено уравнение регрессии: Вывод. По имеющимся статистическим данным для регионов, включенных в наблюдение, наблюдается следующая ситуация: с увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
2. Тесноту линейной связи оценит коэффициент корреляции:
Вывод: наблюдается сильная прямая связь между среднедушевым прожиточным минимумом и среднедневной заработной платой.
Вывод: 52% вариации заработной платы (У) объясняется вариацией среднедушевого прожиточного минимума (фактора Х). Качество модели определяет средняя ошибка аппроксимации: Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
Вывод: Качество построенной модели оценивается как хорошее, так как
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля: a = b = rxy = 0. Рассчитаем t-статистики Стьюдента:
Случайные ошибкипараметров линейной регрессии и коэффициента корреляции определяются по формулам:
Определим случайные ошибки, ma, mb, mrxy
Тогда ta= 77/24,3; tb= 0,92/0,281 = 3,3; trxy= 0,92/0,219 = 3,3
Находим по таблицам tтабл. (0,05; 10) = 2,23, т.к. df = n - 2 = 12 - 2 = 10 и α = 0,05.
Фактические значения t -статистики превосходят табличные значения: ta = 3,2 > tтабл = 2,23, т.е. гипотеза Но отклоняется коэффициент регрессии а статистически значим; tb = 3,3 > tтабл = 2,2,; т.е. гипотеза Но отклоняется коэффициент регрессии b статистически значим;
trxy = 3,3 > tтабл = 2,23, т.е. гипотеза Но отклоняется коэффициент корреляции
Для расчета доверительного интервала определяем предельную ошибкудля каждого показателя:
Таким образом, рассчитаем доверительный интервал для а и b. Для этого определим предельную ошибку для каждого показателя:
Доверительные интервалы:
Вывод: доверительный интервал для коэффициента регрессии а
Вывод: доверительный интервал для коэффициента регрессии b Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью p = 1 – α = 0,95 параметры а и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля. Полученная парная линейная регрессионная модель может быть использована для прогнозирования.
4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Находим сначала точечный прогноз для результативного признака.
Находим прогнозное значение среднедушевого прожиточного минимума: xпрог.= 85,6 * 1,07 = 91,6 руб., тогда прогнозное значение среднедневной заработной платы составит:
Вывод: при прогнозном значении среднедушевого прожиточного минимума, составляющем 107% от среднего уровня, прогнозное значение среднедневной заработной платы составит 161 руб.
5. Вычислим среднюю стандартную ошибку прогноза
где
построим доверительный интервал прогноза:
где Таким образом, ошибка прогноза составит:
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:
Доверительный интервал прогноза:
Вывод: с вероятностью 95% прогноз длясреднедневной заработной платы находится в пределах
Находим диапазон верхней и нижней границ доверительного интервала:
Вывод: выполненный прогноз для среднедневной заработной платы является надежным при заданной вероятности 95% (р = 1 - а = 1 - 0,05 = 0,95), но не совсем точным, так как диапазон верхней и нижней границ доверительного интервала составляет 1,45 (чем ближе к 1, тем лучше прогноз).
[1] Нефтегазовая вертикаль. Аналитический журнал, №5, 2010, с. 96 Практическое занятие. Кривые 2-го порядка: окружность, эллипс, гипербола. Кривой в системе координат называется некоторое множество точек плоскости, координаты которых и только они удовлетворяют уравнению. Уравнение называется при этом общим уравнением кривой. Алгебраической кривой второго порядка в системе координат называется кривая, общее уравнение которой имеет вид:, где числа - не равны нулю одновременно. Существует следующая классификация кривых второго порядка: 1) если, то общее уравнение определяет кривую эллиптического типа (окружность (при,), эллипс (при,), пустое множество, точку); 2) если, то - кривую гиперболического типа (гиперболу, пару пересекающихся прямых); 3) если, то - кривую параболического типа (параболу, пустое множество, прямую, пару параллельных прямых). Окружность, эллипс, гипербола и парабола являются невырожденными кривыми второго порядка. 3. 27 Написать уравнение кривой, расстояние от каждой точки которой до оси Ox вдвое больше расстояния до оси Oy. 3.28 Написать уравнение кривой, расстояние от каждой точки которой до точки 3.29 Найти центр окружности, проходящей через точку 3.30 Установить, что каждое из следующих уравнений определяет окружность, найти ее центр и радиус: а) д) 3.31 Определить, как расположена прямая относительно окружности: пересекает, касается или проходит вне ее, если прямая и окружность заданы уравнениями: а) 3.32 Найти угол между радиусами окружности 3.33 Даны точки 3.34 Окружность касается оси 3.35 Написать каноническое уравнение эллипса, зная, что: а) расстояние между фокусами равно 8, а малая полуось б) большая полуось 3.36.1 Установить, что каждое из следующих уравнений определяет эллипс, найти его центр и построить: а) в) 3.37 Определить, как расположена прямая относительно эллипса: пересекает, касается или проходит вне его, если прямая и эллипс заданы уравнениями: а) 3.38 Написать каноническое уравнение эллипса, у которого расстояния одного из фокусов до концов большой оси равны 5 и 1. 3.39 Эллипс, симметричный относительно осей координат, проходит через точки 3.40 Эллипс, симметричный относительно осей координат, фокусы которого находятся на оси 3.41 Построить гиперболу а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис. 3.42 Написать каноническое уравнение гиперболы, если: а) расстояние между фокусами 3.43.1 Установить, что каждое из следующих уравнений определяет гиперболу, найти ее центр и построить: а) в) 3.44 На гиперболе 3.45 Гипербола симметрична относительно осей координат, проходит через точку 3.46.1 Построить следующие параболы: а) 3.47 Написать уравнение параболы: а) проходящей через точки 3.48.1 Установить, что каждое из следующих уравнений определяет параболу, найти координаты ее вершины А и построить: а) 3.49 На параболе 3.50 Через фокус параболы 3.52 Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы - в вершинах эллипса 3.53 Найти точки пересечения асимптот гиперболы Ответы: 3.27
|




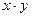
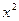

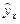


 (руб.)
(руб.)

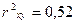
 %
%
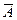 не превышает 8 - 10%.
не превышает 8 - 10%.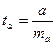 ,
,  и
и 






 статистически значим.
статистически значим.
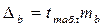
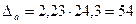


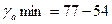 = 23
= 23
 .
.


 .
. =77+0,92*91,6=161 руб.
=77+0,92*91,6=161 руб.





 руб.
руб.
 = 161 ±29,4;
= 161 ±29,4; .
.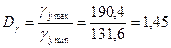
 вдвое меньше расстояния до точки
вдвое меньше расстояния до точки  .
. и касающейся оси абсцисс в точке
и касающейся оси абсцисс в точке 
 г)
г)  ; б)
; б) 
 ; в)
; в)  ; е)
; е)  .
. б)
б) 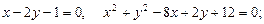 в)
в) 
 проведенными в точки пересечения ее с осью
проведенными в точки пересечения ее с осью 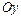 .
. и
и  . Написать уравнение окружности, диаметром которой служит отрезок
. Написать уравнение окружности, диаметром которой служит отрезок  .
. в начале координат и проходит через точку
в начале координат и проходит через точку  . Написать её уравнение и найти точки пересечения с биссектрисами координатных углов.
. Написать её уравнение и найти точки пересечения с биссектрисами координатных углов.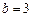 ;
; , а эксцентриситет
, а эксцентриситет  .
.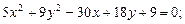 б)
б)  ;
; ; г)
; г) 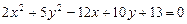 .
. ; б)
; б) 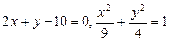 .
. и
и  . Написать его уравнение и найти расстояния точки
. Написать его уравнение и найти расстояния точки  от фокусов.
от фокусов. , проходит через точку
, проходит через точку 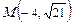 и имеет эксцентриситет
и имеет эксцентриситет  . Написать уравнение эллипса и найти расстояния точки
. Написать уравнение эллипса и найти расстояния точки  Найти:
Найти: , а между вершинами
, а между вершинами 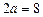 ; б) вещественная полуось
; б) вещественная полуось  , а эксцентриситет
, а эксцентриситет 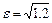 .
. б)
б)  ;
; ; г)
; г) 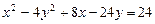 .
. взята точка
взята точка  и имеет мнимую полуось
и имеет мнимую полуось  . Написать ее уравнение и найти расстояния точки
. Написать ее уравнение и найти расстояния точки 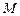 от фокусов.
от фокусов.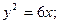 б)
б) 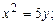 в)
в)  г)
г) 
 ,
, 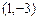 и симметричной относительно
и симметричной относительно  и симметричной относительно
и симметричной относительно  .
. б)
б) 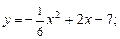 в)
в)  ; г)
; г)  .
. найти точку, фокальный радиус которой равен 4.5.
найти точку, фокальный радиус которой равен 4.5.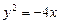 проведена прямая под углом 120° к оси
проведена прямая под углом 120° к оси  .
. с окружностью, имеющей центр в правом фокусе гиперболы, и проходящей через начало координат.
с окружностью, имеющей центр в правом фокусе гиперболы, и проходящей через начало координат. 3.28
3.28  3.29
3.29  3.30 а)
3.30 а)  , б)
, б) 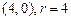 , в)
, в)  , г)
, г) 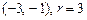 , д)
, д)  , е)
, е)  . 3.31 а) пересекает; б) касается; в) вне окружности. 3.32
. 3.31 а) пересекает; б) касается; в) вне окружности. 3.32  3.33
3.33  3.34
3.34 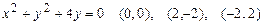 .3.35
.3.35 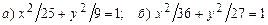 . 3.36.1 а)
. 3.36.1 а) 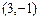 , б)
, б)  , в)
, в)  , г)
, г)  . 3.37 а) пересекает; б) вне эллипса. 3.38
. 3.37 а) пересекает; б) вне эллипса. 3.38  3.39
3.39  . 3.40
. 3.40 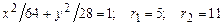 .3.41 а)
.3.41 а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  . 3.42 а)
. 3.42 а) 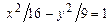 , б)
, б)  . 3.43.1 а)
. 3.43.1 а)  , б)
, б)  , в)
, в)  , г)
, г)  . 3.44
. 3.44  . 3.45
. 3.45  ,
,  . 3.47 а)
. 3.47 а)  , б)
, б)  3.48.1 а) А (2,0), б)
3.48.1 а) А (2,0), б) 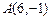 , в) А (1,2), г) А (1,2). 3.49
, в) А (1,2), г) А (1,2). 3.49  3.50
3.50  3.52
3.52 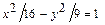 или
или  . 3.53 (0,0)
. 3.53 (0,0)


