Твердые растворы с неограниченной растворимостью
Твердые растворы с неограниченной растворимостью образуются при условиях: – одинаковые типы кристаллических решеток у А и В; – различие в атомных размерах £8 – 15%; – близкое строение валентной оболочки электронов в атоме. Например, Au + Agс ГЦК решеткой или Mo + W.
9. Температурная зависимость удельного сопротивления В идеальном кристалле длина свободного пробега электронов равна бесконечности, а сопротивление электрическому току равно нулю. Подтверждением данного положения является тот факт, что сопротивление чистых отожженных металлов стремится к нулю, когда температура приближается к абсолютному нулю. Свойство электрона свободно перемещаться в идеальной кристаллической решетке не имеет аналога в классической механике. Рассеяние, приводящее к появлению сопротивления, возникает в тех случаях, когда в решетке имеются дефекты строения. Известно, что эффективное рассеяние волн происходит, когда размер рассеивающих центров (дефектов) превышает четверть длины волны. В металлах энергия электронов проводимости составляет 3 – 15 эВ. Этой энергии соответствует длина волны 3 – 70 В чистых металлах совершенной структуры единственной причиной, ограничивающей длину свободного пробега электронов, является тепловое колебание атомов в узлах кристаллической решетки. Электрическое сопротивление металла, обусловленное тепловым фактором, обозначим через rт. Совершенно очевидно, что с ростом температуры увеличиваются амплитуды тепловых колебаний атомов и связанные с ними флуктуации периодического поля решетки. А это, в свою очередь, усиливает рассеяние электронов и вызывает возрастание удельного сопротивления. Чтобы качественно установить характер температурной зависимости удельного сопротивления, воспользуемся следующей упрощенной моделью. Интенсивность рассеяния прямо пропорциональна поперечному сечению сферического объема, который занимает колеблющийся атом, а площадь поперечного сечения пропорциональна квадрату амплитуды тепловых колебаний. Потенциальная энергия атома, отклоненного на D a от узла решетки, определяется выражением
где k упр – коэффициент упругой связи, которая стремится вернуть атом в положение равновесия. Согласно классической статистике средняя энергия одномерного гармонического осциллятора (колеблющегося атома) равна kТ. На этом основании запишем следующее равенство:
Легко доказать, что длина свободного пробега электронов у N атомов обратно пропорциональна температуре:
Необходимо отметить, что полученное отношение не выполняется при низких температурах. Дело в том, что с понижением температуры могут уменьшаться не только амплитуды тепловых колебаний атомов, но и частоты колебаний. Поэтому в области низких температур рассеяние электронов тепловыми колебаниями узлов решетки становится неэффективным. Взаимодействие электрона с колеблющимся атомом лишь незначительно изменяет импульс электрона. В теории колебаний атомов решетки температуру оценивают относительно некоторой характеристической температуры, которую называют температурой Дебая Q D. Температура Дебая определяет максимальную частоту тепловых колебаний, которые могут возбуждаться в кристалле:
Эта температура зависит от сил связи между узлами кристаллической решетки и является важным параметром твердого тела. При T > Q D удельное сопротивление металлов изменяется линейно с температурой (рисунок 8, участок III). Как показывает эксперимент, линейная аппроксимация температурной зависимости rт (T) справедлива и до температур порядка (2/3)Q D, где ошибка не превышает 10%. Для большинства металлов характеристическая температура Дебая не превышает 400 – 450 К. Поэтому линейное приближение обычно справедливо при температурах от комнатной и выше. В низкотемпературной области (T <<Q D), где спад удельного сопротивления обусловлен постепенным исключением все новых и новых частот тепловых колебаний (фононов), теория предсказывает степенную зависимость rт~ T 5. В физике это соотношение известно как закон Блоха – Грюнайзена. Температурный интервал, в котором наблюдается резкая степенная зависимость rт(T), обычно бывает довольно небольшим, причем экспериментальные значения показателя степени лежат в пределах от 4 до 6.
В узкой области I, составляющей несколько кельвинов, у ряда металлов может наступить состояние сверхпроводимости (подробнее ранее) и на рисунке виден скачок удельного сопротивления при температуре T св. У чистых металлов совершенной структуры при стремлении температуры к ОК удельное сопротивление также стремится к 0 (пунктирная кривая), а длина свободного пробега устремляется в бесконечность. Даже при обычных температурах длина свободного пробега электронов в металлах в сотни раз превышает расстояние между атомами (таблица 2). Таблица 2 – Средняя длина свободного пробега электронов
В пределах переходной области II происходит быстрый рост удельного сопротивления r(T), где n может быть до 5 и постепенно убывает с ростом температуры ~ до 1 при T = Q D. Линейный участок (область III) в температурной зависимости r(T) у большинства металлов простирается до температур, близких к точке плавления. Исключение из этого правила составляют ферромагнитные металлы, в которых имеет место дополнительное рассеяние электронов на нарушениях спинового порядка. Вблизи точки плавления, т.е. в области IV, начало которой отмечено на рисунке 7 температурой T нл, и в обычных металлах может наблюдаться некоторое отступление от линейной зависимости. При переходе из твердого состояния в жидкое у большинства металлов наблюдается увеличение удельного сопротивления приблизительно в 1,5 – 2 раза, хотя имеются и необычные случаи: у веществ со сложной кристаллической структурой, подобных висмуту и галлию, плавление сопровождается уменьшением r. Эксперимент выявляет следующую закономерность: если плавление металла сопровождается увеличением объема, то удельное сопротивление скачкообразно возрастает; у металлов с противоположным изменением объема происходит понижение r. При плавлении не происходит существенного изменения ни в числе свободных электронов, ни в характере их взаимодействия. Решающее влияние на изменение r оказывают процессы разупорядочения, нарушение дальнейшего порядка в расположении атомов. Аномалии, наблюдаемые в поведении некоторых металлов (Ga, Bi), могут быть объяснены увеличением модуля сжижаемости при плавлении этих веществ, что должно сопровождаться уменьшением амплитуды тепловых колебаний атомов. Относительное изменение удельного сопротивления при изменении температуры на один кельвин (градус) называют температурным коэффициентом удельного сопротивления:
Положительный знак ar соответствует случаю, когда удельное сопротивление в окрестности данной точки возрастает при повышении температуры. Величина ar также является функцией температуры. В области линейной зависимости r(Т) справедливо выражение:
где r0 и ar – удельное сопротивление и температурный коэффициент удельного сопротивления, отнесенные к началу температурного диапазона, т.е. температуре T 0; r – удельное сопротивление при температуре T. Связь между температурными коэффициентами удельного сопротивления и сопротивления такова:
где ar – температурный коэффициент сопротивления данного резистора; al – температурный коэффициент расширения материала резистивного элемента. У чистых металлов ar >> al, поэтому у них ar» aR. Однако для термостабильных металлических сплавов такое приближение оказывается несправедливым.
10. Влияние примесей и других структурных дефектов Как отмечалось, причинами рассеяния электронных волн в металле являются не только тепловые колебания узлов решетки, но и статические дефекты структуры, которые также нарушают периодичность потенциального поля кристалла. Рассеяние на статических дефектах структуры не зависит от температуры. Поэтому по мере приближения температуры к абсолютному нулю сопротивление реальных металлов стремится к некоторому постоянному значению, называемому остаточным сопротивлением (см. рисунок 8). Отсюда вытекает правило Маттиссена об аддитивности удельного сопротивления:
т.е. полное удельное сопротивление металла есть сумма удельного сопротивления, обусловленного рассеянием электронов на тепловых колебаниях узлов кристаллической решетки, и остаточного удельного сопротивления, обусловленного рассеянием электронов на статических дефектов структуры. Исключение из этого правила составляют сверхпроводящие металлы, в которых сопротивление исчезает ниже некоторой критической температуры. Наиболее существенный вклад в остаточное сопротивление вносит рассеяние на примесях, которые всегда присутствуют в реальном проводнике либо в виде загрязнения, либо в виде легирующего (т.е. преднамеренно вводимого) элемента. Следует заметить, что любая примесная добавка приводит к повышению r, даже если она обладает повышенной проводимостью по сравнению с основным металлом. Так, введение в медный проводник 0,01 ат. доли примеси серебра вызывает увеличение удельного сопротивления меди на 0,002мкОм ×м. Экспериментально установлено, что при малом содержании примесей удельное сопротивление возрастает пропорционально концентрации примесных атомов. Иллюстрацией правила Маттиссена является рисунок 9, из которого видно, что температурные зависимости удельного сопротивления чистой меди и ее сплавов с малым количеством (приблизительно до 4 ат. %) индия, сурьмы, олова, мышьяка взаимно параллельны. Различные примеси по-разному влияют на остаточное сопротивление металлических проводников. Эффективность примесного рассеяния определяется возмущающим потенциалом в решетке, значение которого тем выше, чем сильнее различаются валентности примесных атомов и металла – растворителя (основы). Для одновалентных металлов изменение остаточного сопротивления на 1 ат.% примеси ("примесный" коэффициент электросопротивления) подчиняется правилу Линде:
где a и b – константы, зависящие от природы металла и периода, который занимает в Периодической системе элементов примесный атом; D Z – разность валентностей металла – растворителя и примесного атома. Из (15) следует, что влияние металлоидных примесей на снижение проводимости сказывается сильнее, чем влияние примесей металлических элементов.
Помимо примесей некоторый вклад в остаточное сопротивление, вносят собственные дефекты структуры – вакансии, атомы внедрения, дислокации, границы зерен. Концентрация точечных дефектов экспоненциально возрастает с температурой и может достигать высоких значений вблизи точки плавления. Кроме того, вакансии и междуузельные атомы легко возникают в материале при его облучении частицами высокой энергии, например, нейтронами из реактора или ионами из ускорителя. По измеренному значению сопротивления можно судить о степени радиационного повреждения решетки. Таким же образом можно проследить и за восстановлением (отжигом) облученного образца. Изменение остаточного сопротивления меди на 1 ат.% точечных дефек тов составляет: в случае вакансий 0,010 – 0,015 мкОм × Ом; в случае атомов внедрения 0,005 – 0,010 мкОм × Ом. Остаточное сопротивление представляет собой весьма чувствительную характеристику химической чистоты и структурного совершенства металлов. На практике при работе с металлами особо высокой чистоты для оценки содержания примесей измеряют отношение удельных сопротивлений при комнатной температуре и температуре жидкого гелия:
Чем чище металл, тем больше значение b. В наиболее чистых металлах, получаемых в настоящее время (со степенью чистоты 99,99999%), параметр b имеет значение порядка 105. Большое влияние на удельное сопротивление металлов и сплавов оказывают искажения, вызываемые напряженным состоянием. Однако степень этого влияния определяется характером напряжений. Например, при всестороннем сжатии у большинства металлов удельное сопротивление уменьшается. Это объясняется сближением атомов и уменьшением амплитуды тепловых колебаний решетки. Пластическая деформация и наклеп всегда повышают удельное сопротивление металлов и сплавов. Однако это повышение даже при значительном наклепе чистых металлов составляет единицы процентов. Термическая закалка приводит к повышению r, что связано с искажениями решетки, появлением внутренних напряжений. При рекристаллизации путем термической обработки (отжига) удельное сопротивление может быть снижено до первоначального значения, поскольку происходит "залечивание" дефектов и снятие внутренних напряжений.
|

 . Поэтому любые микронеоднородности структуры препятствуют распространению электронных волн, вызывают рост удельного сопротивления материала.
. Поэтому любые микронеоднородности структуры препятствуют распространению электронных волн, вызывают рост удельного сопротивления материала. , (9)
, (9)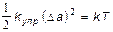 .
. . (10)
. (10) .
.
 . (11)
. (11) , (12)
, (12) , (13)
, (13) , (14)
, (14)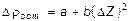 , (15)
, (15)




