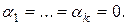1) Если 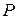 − поле и
− поле и  , то
, то  имеем
имеем 
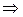
 − векторное пространство, называемое нулевым.
− векторное пространство, называемое нулевым.
2)  − векторное пространство комплексных чисел над полем вещественных чисел.
− векторное пространство комплексных чисел над полем вещественных чисел.  − векторное пространство вещественных чисел над полем рациональных чисел.
− векторное пространство вещественных чисел над полем рациональных чисел.
3) Множество  матриц размера
матриц размера  образует векторное пространство
образует векторное пространство  .
.
4) Множество многочленов степени не выше n образует векторное пространство  .
.
5) Множество  непрерывных на
непрерывных на  функций образует векторное пространство
функций образует векторное пространство  .
.
6)  – n -мерное координатное пространство (или арифметическое пространство), элементами которого являются упорядоченные наборы из n чисел:
– n -мерное координатное пространство (или арифметическое пространство), элементами которого являются упорядоченные наборы из n чисел: 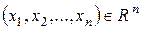 . Операции определены следующим образом:
. Операции определены следующим образом:
 ;
;
 .
.
Задача. Проверить выполнение аксиом векторного пространства.
2о. Линейно зависимые и линейно независимые системы векторов
Это понятие является обобщением понятия линейной зависимости строк.
Определение 2. Линейной комбинацией векторов 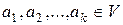 с коэффициентами
с коэффициентами  называется выражение вида:
называется выражение вида:  .
.
Определение 3. Вектора 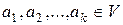 называются линейно независимыми, если
называются линейно независимыми, если  , из которых хотя бы одно отлично от нуля, т.е. линейная комбинация
, из которых хотя бы одно отлично от нуля, т.е. линейная комбинация  с этими
с этими  является нулевым вектором V, т.е.
является нулевым вектором V, т.е.  . Вектора
. Вектора  , не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами,
, не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами, 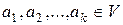 называются линейно независимыми, если их линейная комбинация является нулевым элементом V лишь при условии, что
называются линейно независимыми, если их линейная комбинация является нулевым элементом V лишь при условии, что 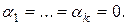

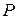 − поле и
− поле и  , то
, то  имеем
имеем 
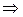
 − векторное пространство, называемое нулевым.
− векторное пространство, называемое нулевым. − векторное пространство комплексных чисел над полем вещественных чисел.
− векторное пространство комплексных чисел над полем вещественных чисел.  − векторное пространство вещественных чисел над полем рациональных чисел.
− векторное пространство вещественных чисел над полем рациональных чисел. матриц размера
матриц размера  образует векторное пространство
образует векторное пространство  .
. .
. непрерывных на
непрерывных на  функций образует векторное пространство
функций образует векторное пространство  .
. – n -мерное координатное пространство (или арифметическое пространство), элементами которого являются упорядоченные наборы из n чисел:
– n -мерное координатное пространство (или арифметическое пространство), элементами которого являются упорядоченные наборы из n чисел: 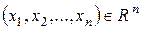 . Операции определены следующим образом:
. Операции определены следующим образом: ;
; .
.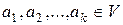 с коэффициентами
с коэффициентами  называется выражение вида:
называется выражение вида:  .
. , из которых хотя бы одно отлично от нуля, т.е. линейная комбинация
, из которых хотя бы одно отлично от нуля, т.е. линейная комбинация  с этими
с этими  является нулевым вектором V, т.е.
является нулевым вектором V, т.е.  . Вектора
. Вектора