1) Для того, чтобы элементы 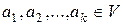 были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов был линейной комбинацией остальных.
были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов был линейной комбинацией остальных.
2) Если среди  один элемент нулевой, то они линейно зависимы.
один элемент нулевой, то они линейно зависимы.
3) Если часть элементов множества  линейно зависима, то и все элементы линейно зависимы.
линейно зависима, то и все элементы линейно зависимы.
Доказательство. 1о Аналогично доказательству из §8.
2о Если 
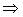
 и
и  – любое, например,
– любое, например, 
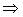
 линейно зависимы.
линейно зависимы.
3о Если  – линейно зависимы, то
– линейно зависимы, то  одновременно неравные нулю, так что
одновременно неравные нулю, так что 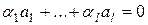
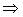
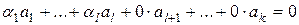 и хотя бы одно из
и хотя бы одно из  отлично от нуля
отлично от нуля 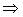
 линейно зависимы. ч.т.д.
линейно зависимы. ч.т.д.
Пример. Рассмотрим линейное пространства  и докажем, что n элементов из
и докажем, что n элементов из  вида
вида  ,
,  ,…,
,…,  линейно независимы, а добавление еще одного элемента
линейно независимы, а добавление еще одного элемента  приводит к линейно зависимой системе. Действительно, рассмотрим линейную комбинацию
приводит к линейно зависимой системе. Действительно, рассмотрим линейную комбинацию  с
с 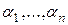 . Имеем
. Имеем  . Вектор справа равен нулю, если все
. Вектор справа равен нулю, если все  , т.е.
, т.е.  – линейно независимы.
– линейно независимы.
Добавим  . Тогда по теореме 1, п. 1о, достаточно показать, что x – линейная комбинация
. Тогда по теореме 1, п. 1о, достаточно показать, что x – линейная комбинация  . Действительно,
. Действительно, 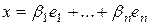 .
.
3о. Базис линейного пространства и координаты вектора в базисе.
Def 5. Совокупность векторов  называют базисом в
называют базисом в  , если
, если
1о. вектора 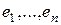 – линейно независимы;
– линейно независимы;
2о. для  найдутся
найдутся 
 . (1)
. (1)
При этом равенство (1) называется разложением элемента  по базису
по базису 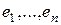 , а
, а 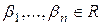 называются координатами
называются координатами  относительно базиса
относительно базиса 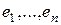 .
.
Теорема 2 (о единственности разложения по базису). Любой элемент  может быть единственным образом разложен по базису
может быть единственным образом разложен по базису 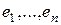 , т.е. координаты вектора относительно базиса определяются однозначно.
, т.е. координаты вектора относительно базиса определяются однозначно.
Доказательство. Пусть  и
и  . Тогда
. Тогда  . В силу линейной независимости
. В силу линейной независимости 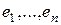
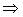
 . ч.т.д.
. ч.т.д.
Теорема 3 (операции над векторами, заданными своими координатами). При сложении любых двух векторов  и
и  их координаты (относительно любого фиксированного базиса в
их координаты (относительно любого фиксированного базиса в  ) складываются; при умножении
) складываются; при умножении  на
на 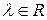 , все координаты вектора умножаются на это число.
, все координаты вектора умножаются на это число.
Доказательство. Пусть  - базис в
- базис в  ,
,  ,
,  . Тогда в силу аксиом линейного пространства
. Тогда в силу аксиом линейного пространства  ,
,  . В силу единственности разложения по базису
. В силу единственности разложения по базису 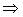 что теорема доказана.
что теорема доказана.
Примеры. 1о. Базис в  - любое ненулевое число.
- любое ненулевое число.
2о. 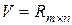 . Базис образуют матрицы
. Базис образуют матрицы  ,
, 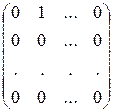 , …,
, …,  с одним единичным элементом.
с одним единичным элементом.
3о.  – множество многочленов степени не выше n. Базис:
– множество многочленов степени не выше n. Базис:  ,
,  , …,
, …,  .
.
4о.  – см. выше.
– см. выше.
4о. Размерность линейного пространства.
Def 6. Линейное пространство  называется n -мерным, если
называется n -мерным, если
1о. В нем  n линейно независимых векторов.
n линейно независимых векторов.
2о.  векторов линейно зависимы.
векторов линейно зависимы.
Тогда n называется размерностью  и обозначается
и обозначается  .
.
Def 7. Линейное пространство называется бесконечномерным, если в нем  любое число линейно независимых векторов.
любое число линейно независимых векторов.
Выясним связь между понятием базиса и размерности линейного пространства.
Теорема 4. Если  – линейное пространство размерности n, то
– линейное пространство размерности n, то  линейно независимых векторов этого пространства образуют его базис.
линейно независимых векторов этого пространства образуют его базис.
Доказательство. Пусть 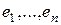 – система n линейно независимых векторов из
– система n линейно независимых векторов из  . Если
. Если  - любой вектор из
- любой вектор из  , то по Def 6, вектора
, то по Def 6, вектора  – линейно зависимы, т.е.
– линейно зависимы, т.е. 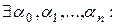

и среди 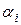 есть хотя бы одно отличное от нуля. Очевидно, что
есть хотя бы одно отличное от нуля. Очевидно, что  (т. к. иначе
(т. к. иначе 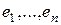 – линейно зависимы)
– линейно зависимы) 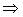
 , т.е.
, т.е.
 – линейная комбинация
– линейная комбинация 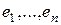
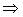 т. к.
т. к.  – произвольный, то
– произвольный, то 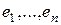 –базис.
–базис.
Теорема 5. Если  имеет базис, состоящий из n элементов, то
имеет базис, состоящий из n элементов, то  .
.
Доказательство. Пусть 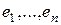 – базис в
– базис в  . Достаточно показать, что
. Достаточно показать, что  векторов
векторов  линейно зависимы. Разложим их по базису:
линейно зависимы. Разложим их по базису:
 ,
,
…
 ,
,
где  .
.
Очевидно, что линейная зависимость векторов  эквивалентна линейной зависимости строк матрицы
эквивалентна линейной зависимости строк матрицы
 .
.
Но строки этой матрицы заведомо линейно зависимы, т. к. порядок базисного минора не превосходит n и хотя бы одна из  строк не является базисной, и по теореме о базисном миноре представляет собой линейную комбинацию базисных строк (а стало быть и остальных).
строк не является базисной, и по теореме о базисном миноре представляет собой линейную комбинацию базисных строк (а стало быть и остальных).
Примеры. 1о.  . 2о.
. 2о.  . 3о.
. 3о.  . 4о.
. 4о.  . 5о.
. 5о. 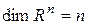 .
.
5о. Изоморфизм линейных пространств.
Здесь будет показано, что линейные пространства одной и той же размерности в смысле некоторых свойств, связанных с введенными операциями, не отличаются друг от друга.
Def 6. Два произвольных линейных пространства V и  над одним и тем же полем
над одним и тем же полем 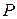 называются изоморфными, если между элементами этих пространств можно установить взаимнооднозначное соответствие так, что если векторам
называются изоморфными, если между элементами этих пространств можно установить взаимнооднозначное соответствие так, что если векторам 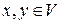 отвечают соответственные вектора
отвечают соответственные вектора  , то вектору
, то вектору  отвечает вектор
отвечает вектор  , а вектору
, а вектору  при
при  отвечает вектор
отвечает вектор  .
.
Свойства изоморфных пространств.
10. Нулевому элементу V соответствует нулевой элемент  и наоборот.
и наоборот.
Док-во: Если  .
.
20. Если элементам 
 соответствуют
соответствуют  , то линейная комбинация векторов
, то линейная комбинация векторов  равна нулю V, т.е.
равна нулю V, т.е.  линейная комбинация
линейная комбинация 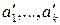 с теми же коэффициентами
с теми же коэффициентами  равна нулю, т.е.
равна нулю, т.е.  .
.
Док-во следует из 10.
30. Если V и  изоморфны, то максимальное число линейно независимых векторов в каждом из пространств одно и тоже, т.е. два изоморфных пространства имеют одну и туже размерность.
изоморфны, то максимальное число линейно независимых векторов в каждом из пространств одно и тоже, т.е. два изоморфных пространства имеют одну и туже размерность.
40. Пространства разных размерностей не могут быть изоморфными.
Теорема 6. Любые два n-мерных линейных пространства V и  над одним и тем же полем
над одним и тем же полем 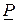 изоморфны.
изоморфны.
Док-во. Выберем в V базис  − базис
− базис  Каждому элементу
Каждому элементу  , поставим в соответствие элемент
, поставим в соответствие элемент  с теми же координатами
с теми же координатами  в базисе
в базисе  .
.
Однако это соответствие взаимнооднозначно, т.к.  имеет единственным образом определенные координаты
имеет единственным образом определенные координаты 
 , которые в свою очередь, определяют единственный элемент
, которые в свою очередь, определяют единственный элемент 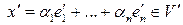 .
.
В силу равноправности V и  ,
,  соответствует единственный
соответствует единственный  . Легко видеть, что если
. Легко видеть, что если 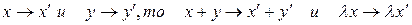 в силу введенного соответствия.
в силу введенного соответствия.
Т.о., все линейные пространства данной размерности n-ная полем 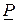 изоморфны, т.е. их свойства, связанные с линейными операциями неразличимы.
изоморфны, т.е. их свойства, связанные с линейными операциями неразличимы.

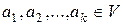 были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов был линейной комбинацией остальных.
были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов был линейной комбинацией остальных. один элемент нулевой, то они линейно зависимы.
один элемент нулевой, то они линейно зависимы.
 и
и  – любое, например,
– любое, например, 
 одновременно неравные нулю, так что
одновременно неравные нулю, так что 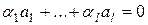
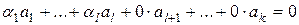 и хотя бы одно из
и хотя бы одно из  отлично от нуля
отлично от нуля  и докажем, что n элементов из
и докажем, что n элементов из  ,
,  ,…,
,…,  линейно независимы, а добавление еще одного элемента
линейно независимы, а добавление еще одного элемента  приводит к линейно зависимой системе. Действительно, рассмотрим линейную комбинацию
приводит к линейно зависимой системе. Действительно, рассмотрим линейную комбинацию  с
с 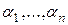 . Имеем
. Имеем  . Вектор справа равен нулю, если все
. Вектор справа равен нулю, если все  , т.е.
, т.е.  . Тогда по теореме 1, п. 1о, достаточно показать, что x – линейная комбинация
. Тогда по теореме 1, п. 1о, достаточно показать, что x – линейная комбинация 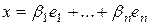 .
. называют базисом в
называют базисом в  , если
, если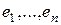 – линейно независимы;
– линейно независимы; найдутся
найдутся 
 . (1)
. (1) по базису
по базису 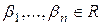 называются координатами
называются координатами  относительно базиса
относительно базиса  и
и  . Тогда
. Тогда  . В силу линейной независимости
. В силу линейной независимости  . ч.т.д.
. ч.т.д. их координаты (относительно любого фиксированного базиса в
их координаты (относительно любого фиксированного базиса в 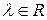 , все координаты вектора умножаются на это число.
, все координаты вектора умножаются на это число. . Тогда в силу аксиом линейного пространства
. Тогда в силу аксиом линейного пространства  ,
,  . В силу единственности разложения по базису
. В силу единственности разложения по базису  - любое ненулевое число.
- любое ненулевое число. . Базис образуют матрицы
. Базис образуют матрицы  ,
, 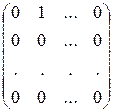 , …,
, …,  – множество многочленов степени не выше n. Базис:
– множество многочленов степени не выше n. Базис:  ,
,  .
. n линейно независимых векторов.
n линейно независимых векторов. векторов линейно зависимы.
векторов линейно зависимы. .
. линейно независимых векторов этого пространства образуют его базис.
линейно независимых векторов этого пространства образуют его базис. – линейно зависимы, т.е.
– линейно зависимы, т.е. 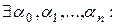

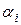 есть хотя бы одно отличное от нуля. Очевидно, что
есть хотя бы одно отличное от нуля. Очевидно, что  (т. к. иначе
(т. к. иначе  , т.е.
, т.е. линейно зависимы. Разложим их по базису:
линейно зависимы. Разложим их по базису: ,
, ,
, .
. эквивалентна линейной зависимости строк матрицы
эквивалентна линейной зависимости строк матрицы .
. строк не является базисной, и по теореме о базисном миноре представляет собой линейную комбинацию базисных строк (а стало быть и остальных).
строк не является базисной, и по теореме о базисном миноре представляет собой линейную комбинацию базисных строк (а стало быть и остальных). . 2о.
. 2о.  . 3о.
. 3о.  . 4о.
. 4о.  . 5о.
. 5о. 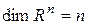 .
. над одним и тем же полем
над одним и тем же полем 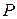 называются изоморфными, если между элементами этих пространств можно установить взаимнооднозначное соответствие так, что если векторам
называются изоморфными, если между элементами этих пространств можно установить взаимнооднозначное соответствие так, что если векторам 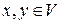 отвечают соответственные вектора
отвечают соответственные вектора  , то вектору
, то вектору  отвечает вектор
отвечает вектор  , а вектору
, а вектору  при
при  отвечает вектор
отвечает вектор  .
. .
.
 соответствуют
соответствуют  , то линейная комбинация векторов
, то линейная комбинация векторов  линейная комбинация
линейная комбинация 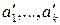 с теми же коэффициентами
с теми же коэффициентами  равна нулю, т.е.
равна нулю, т.е.  .
.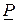 изоморфны.
изоморфны. − базис
− базис  Каждому элементу
Каждому элементу  , поставим в соответствие элемент
, поставим в соответствие элемент  с теми же координатами
с теми же координатами  в базисе
в базисе  .
. имеет единственным образом определенные координаты
имеет единственным образом определенные координаты 
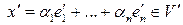 .
. соответствует единственный
соответствует единственный  . Легко видеть, что если
. Легко видеть, что если 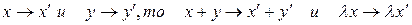 в силу введенного соответствия.
в силу введенного соответствия.


