Свойства эллипса

1. Характеристика движений мамбо

2. Темп исполнеия

 

 

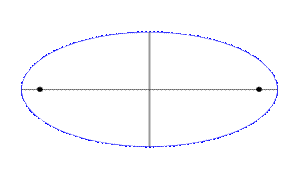
Эллипс

Э́ллипс (др.-греч. ἔλλειψις – опущение, недостаток, в смысле недостатка эксцентриситета до 1) – геометрическое место точек M плоскости, для которых сумма расстояний до двух данных точек F ₁ и F ₂ (называемых фокусами) постоянна и больше расстояния между фокусами, то есть | F ₁M| + | F ₂M| = 2 a, причем | F ₁ F ₂| < 2 a.

Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением.

Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.

 

Проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2 a в вышеприведённом уравнении.

Отрезок C D, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.

Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.

Точка пересечения большой и малой осей эллипса называется его центром.

Расстояния r₁ и r₂ от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.

Расстояние с = называется фокальным расстоянием.

Величина называется эксцентриситетом.

Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.

Радиус эллипса в данной точке (расстояние от его центра до данной точки) вычисляется по формуле

,

где – угол между радиус-вектором данной точки и осью абсцисс.

Фокальным параметром p = называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.

Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью: k = . Величина, равная 1 – k = называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие – нулю. Коэффициент сжатия и эксцентриситет эллипса связаны соотношением k ² = 1 – e ².

Для каждого из фокусов существует прямая, называемая директрисой, такая, что отношение расстояния от произвольной точки эллипса до его фокуса к расстоянию от этой точки до данной прямой равно эксцентриситету эллипса. Весь эллипс лежит по ту же сторону от такой прямой, что и фокус. Уравнения директрис эллипса в каноническом виде записываются как x = для фокусов соответственно. Расстояние между фокусом и директрисой равно .

Свойства эллипса

Оптические свойства. Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе. Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.

Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.

Точки пересечения эллипса с осями являются его вершинами.

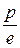Эксцентриситет эллипса равен отношению Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.