Задача 3. Выполнить действия над матрицами .
Задача 4. Решить матричное уравнение.
Задача 5. Решить систему однородных уравнений, выделив какой-нибудь фундаментальный набор решений: 1. 3. 5. 7.
9.
11.
13.
15.
17.
19.
21.
23.
25.
27.
29.
Решение варианта Задача 1. Доказать совместность данной системы линейных уравнений и решить ее методом Гаусса:
Решение. Произведем элементарные преобразования над строчками расширенной матрицы системы, приводя ее к ступенчатому виду:
Для упрощения дальнейших вычислений сначала из второй строки вычитаем первую, оставив без изменения все строчки, кроме первой. Затем первую строку устно умножаем на –3 и складываем со второй, потом – на –4 и складываем с третьей строкой, и, наконец, на –2 и прибавляем к четвертой строке. В результате все элементы первого столбца, кроме единицы, стоящей в первой строке, равны нулю. Сравнивая элементы второго столбца, видим, что имеется возможность получить единицу во втором столбце и второй строке, если из второй строки вычесть четвертую (что снова упростит дальнейшие вычисления):
Умножим вторую строку на –14 и прибавим ее к третьей строке, затем – на –4 и прибавим к четвертой строке. Так получены нулевые элементы второго столбца, расположенные ниже главной диагонали. Осталось умножить третью строку на –13 и прибавить к четвертой, предварительно умноженной на 23. В результате ниже главной диагонали расширенной матрицы имеем нули, значит, матрица приведена к треугольному виду. На этом закончен прямой ход метода Гаусса. На этом этапе удобно провести исследование системы на совместность, для чего определим ранг прямой и расширенной матрицы системы. Количество ненулевых элементов главной диагонали равно 4, значит, ранг основной матрицы равен 4. Очевидно, ранг расширенной матрицы тоже равен 4.Система совместна, причем имеет единственное решение, так как число неизвестных совпадает с рангом матрицы. С помощью обратного хода найдем это решение. Полученная матрица соответствует системе:
Из последней строки найдем Задача 2. Решить систему двумя способами: 1) по формулам Крамера; 2) методом обратной матрицы.
Решение. Вычислим определитель системы:
Так как
Находим решение системы:
Найдем решение системы методом обратной матрицы. Определяем алгебраические дополнения элементов матрицы системы:
Решение системы уравнений определяем по формуле где
Таким образом, Задача 3. Выполнить действия над матрицами где
|




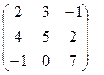















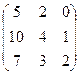

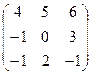






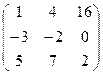












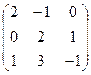






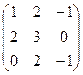






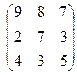



















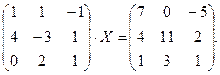



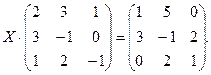



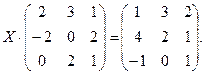






 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
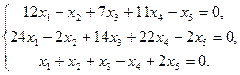 10.
10. 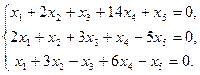
 12.
12. 
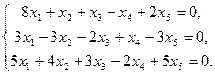 14.
14. 
 16.
16. 
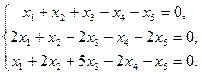 18.
18. 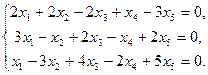
 20.
20. 
 22.
22. 
 24.
24. 
 26.
26. 
 28.
28. 
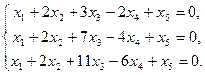 30.
30. 

 ~
~  ~
~  ~
~ ~
~  ~
~ 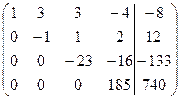

 , подставим найденное значение в третью строку и получим
, подставим найденное значение в третью строку и получим  из второй строки найдем
из второй строки найдем  из первой –
из первой –  .
.

 , система имеет единственное решение. Для нахождения этого решения по формулам Крамера вычислим вспомогательные определители:
, система имеет единственное решение. Для нахождения этого решения по формулам Крамера вычислим вспомогательные определители: ,
,  ,
,  .
. ,
, 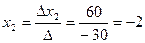 ,
,  .
.






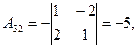


 ,
,  ,
,  .
. .
. .
.




