Гладкая поверхность  в трехмерном пространстве называется двусторонней, если нормаль к поверхности при обходе по любому замкнутому контуру, лежащему на поверхности
в трехмерном пространстве называется двусторонней, если нормаль к поверхности при обходе по любому замкнутому контуру, лежащему на поверхности  и не имеющему общих точек с ее границей, возвращается в первоначальное положение. Выбор направления нормали называется ориентацией поверхности.
и не имеющему общих точек с ее границей, возвращается в первоначальное положение. Выбор направления нормали называется ориентацией поверхности.
Понятие поверхностного интеграла 2-го рода вводится следующим образом.
Пусть  – кусочно-гладкая ориентированная поверхность и
– кусочно-гладкая ориентированная поверхность и
 –
–
векторное поле, заданное в окрестности поверхности  . Разобьем поверхность
. Разобьем поверхность  на частичный поверхности
на частичный поверхности  , площади которых обозначим через
, площади которых обозначим через  . Для каждой области
. Для каждой области  составим произведение
составим произведение
 ,
,
где  – произвольная точка поверхности
– произвольная точка поверхности  , а
, а  – вектор единичной нормали в этой точке. Из этих произведений можно составить интегральные суммы
– вектор единичной нормали в этой точке. Из этих произведений можно составить интегральные суммы
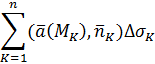
и подсчитать их предел при  .
.
Если этот предел существует и не зависит от способа разбиения поверхности  на частичные поверхности, а так же от выбора точек
на частичные поверхности, а так же от выбора точек  , то этот предел называется поверхностным интегралом 2-го рода и обозначается
, то этот предел называется поверхностным интегралом 2-го рода и обозначается
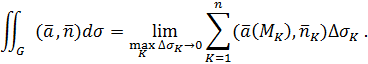
Если поле  непрерывно на поверхности
непрерывно на поверхности  , то этот интеграл существует.
, то этот интеграл существует.
Пусть  является векторным полем скоростей частиц движущейся жидкости. Тогда поверхностный интеграл 2-го рода определяет количество жидкости, протекающей через поверхность
является векторным полем скоростей частиц движущейся жидкости. Тогда поверхностный интеграл 2-го рода определяет количество жидкости, протекающей через поверхность  в данном направлении в единицу времени. Поэтому поверхностный интеграл второго рода часто называют потоком векторного поля через заданную поверхность. Переход к другой стороне поверхности меняет направление нормали к поверхности, а поэтому и знак интеграла.
в данном направлении в единицу времени. Поэтому поверхностный интеграл второго рода часто называют потоком векторного поля через заданную поверхность. Переход к другой стороне поверхности меняет направление нормали к поверхности, а поэтому и знак интеграла.
Вычисление поверхностного интеграла 2-го рода сводится к вычислению двойных интегралов. В самом деле, пусть
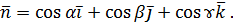
Тогда

Вычислим первый интеграл из правой части  . Для этого рассмотрим два случая.
. Для этого рассмотрим два случая.
1)  на
на  . Тогда очевидно, что
. Тогда очевидно, что  как интеграл от нулевой функции.
как интеграл от нулевой функции.
2) Пусть  – знакопостоянная функция на поверхности
– знакопостоянная функция на поверхности  , то есть
, то есть  на всей поверхности
на всей поверхности  . Это означает, что поверхность
. Это означает, что поверхность  можно однозначно спроектировать на плоскость
можно однозначно спроектировать на плоскость  . Обозначим через
. Обозначим через  проекцию на эту плоскость. Тогда, если
проекцию на эту плоскость. Тогда, если  , то есть угол образованный нормалью к поверхности
, то есть угол образованный нормалью к поверхности  с осью
с осью 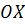 острый, то по правилу вычисления поверхностного интеграла 1-го рода, изложенному в предыдущем разделе, получаем
острый, то по правилу вычисления поверхностного интеграла 1-го рода, изложенному в предыдущем разделе, получаем
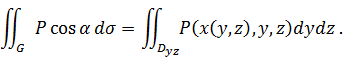
Если же  на
на  , то угол между нормалью и осью
, то угол между нормалью и осью  тупой, и поэтому
тупой, и поэтому

Все три приведенные выше равенства можно записать одной формулой:

где  , если
, если  во всех точках
во всех точках  ,
,  , если
, если  на
на  и
и  , если
, если  на
на  .
.
Применяя последнюю формулу к остальным интегралам в правой части равенства  , получаем соотношение
, получаем соотношение


Заметим, что формула  получена в предложении, что каждая из координат вектора нормали
получена в предложении, что каждая из координат вектора нормали  либо знакопостоянна всюду на поверхности
либо знакопостоянна всюду на поверхности  , либо тождественно равна нулю на этой поверхности.
, либо тождественно равна нулю на этой поверхности.
Если поверхность  не удовлетворяет приведенному условию, то для вычисления поверхностного интеграла 2-го рода по этой поверхности надо сначала разбить его на несколько частей, каждая из которых обладает указанным свойством, а затем применить к каждой из этих частей формулу
не удовлетворяет приведенному условию, то для вычисления поверхностного интеграла 2-го рода по этой поверхности надо сначала разбить его на несколько частей, каждая из которых обладает указанным свойством, а затем применить к каждой из этих частей формулу 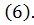
 Пример 3. Найти поток векторного поля
Пример 3. Найти поток векторного поля
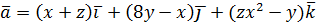
через часть параболического цилиндра  , на которой
, на которой  ,
,
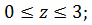
положительную сторону поверхности выбрать так, чтобы нормаль к ней образовала острый угол с осью
.
Решение. Так как вектор нормали образует (см. Рис.3) острый угол с осью  то
то  Кроме того, очевидно, что
Кроме того, очевидно, что  и
и  Поэтому формула
Поэтому формула  принемает в данном случае следующий вид:
принемает в данном случае следующий вид:
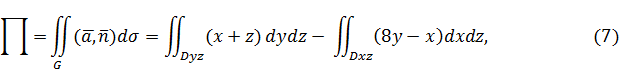
где
 и
и
 -
-
- проекции поверхности  на плоскости
на плоскости  и
и  соответственно.
соответственно.
Вычислим отдельно каждый из двух интегралов из правой части 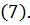
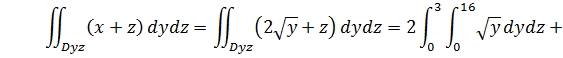
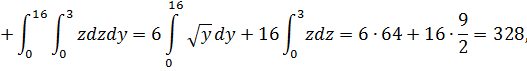
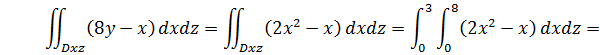
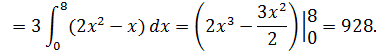
Подставляя эти результаты в 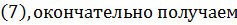
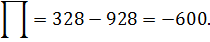
Пример 4. Найти поток векторного поля
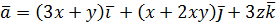
Через полную поверхность конуса, ограниченного поверхностями
 и
и  Положительным считается направление внешней нормали.
Положительным считается направление внешней нормали.
 Решение. Так как
Решение. Так как
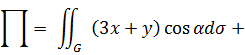
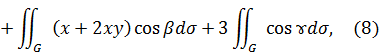
то надо вычислить каждый из трёх интегралов в правой части
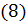
. Прежде чем вычислять, заметим, что полная поверхность

конуса состоит из двух частей:
 и
и

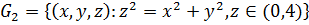
(см. Рис.4).
При этом на  вектором внешней нормали является вектор
вектором внешней нормали является вектор  а на
а на
 - вектор
- вектор 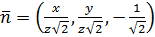

1) Вычислим третий интеграл в правой части
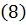
. Учитывая знак

на  и
и 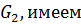



где  - проекция поверхностей
- проекция поверхностей  и
и  на плоскость
на плоскость 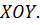
2) Вычислим второй интеграл в правой части 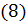 .
.
Так как  на
на  , то
, то
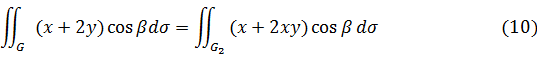
Заметим, что  не является знакопостоянной функцией на всей поверхности
не является знакопостоянной функцией на всей поверхности  . Поэтому разобьем
. Поэтому разобьем  на две части:
на две части:
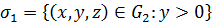 и
и  .
.
Тогда  на
на  и
и 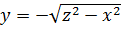 на
на  . Поэтому
. Поэтому  на
на  и
и  на
на  . Обе поверхности
. Обе поверхности  однозначно проектируются на область
однозначно проектируются на область
 (см. Рис.6)
(см. Рис.6)
Поэтому из  следует, что
следует, что
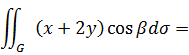
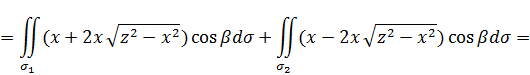
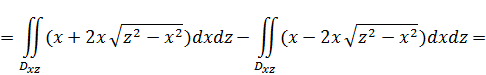
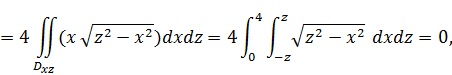
как интеграл от нечетной по 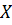 функции по симметричному отрезку.
функции по симметричному отрезку.
3) Вычислим первый интеграл из правой части 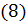 .
.
Так как  на
на  , то
, то

Разобьем  на две части:
на две части:  и
и  . Тогда
. Тогда  на
на  и
и 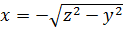 на
на  .
.
Кроме того,  на
на  и
и  на
на  . Поэтому, учитывая
. Поэтому, учитывая  , получаем
, получаем
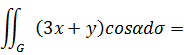

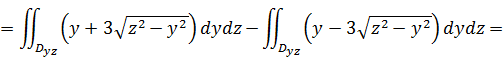

где 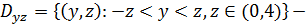
 проекция поверхностей
проекция поверхностей  и
и  на плоскость
на плоскость  (см. Рис. 5). Переходя в
(см. Рис. 5). Переходя в  к повторному интегралу, получаем
к повторному интегралу, получаем
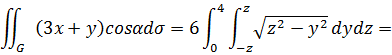
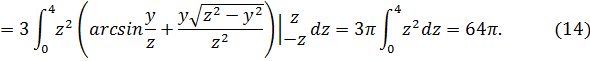
Учитывая  окончательно имеем
окончательно имеем
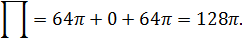
Контрольное задание
В задачах 1 и 2найти поверхностный интеграл первого рода по поверхности  от скалярного поля
от скалярного поля 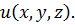
В задачах 3 и 4 найти поток векторного поля  через поверхность
через поверхность  в заданном направлении
в заданном направлении  .
.
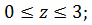 положительную сторону поверхности выбрать так, чтобы нормаль к ней образовала острый угол с осью
положительную сторону поверхности выбрать так, чтобы нормаль к ней образовала острый угол с осью 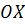 .
.
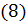 . Прежде чем вычислять, заметим, что полная поверхность
. Прежде чем вычислять, заметим, что полная поверхность  конуса состоит из двух частей:
конуса состоит из двух частей:
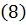 . Учитывая знак
. Учитывая знак 


 –
– , площади которых обозначим через
, площади которых обозначим через  . Для каждой области
. Для каждой области  составим произведение
составим произведение ,
, – произвольная точка поверхности
– произвольная точка поверхности  – вектор единичной нормали в этой точке. Из этих произведений можно составить интегральные суммы
– вектор единичной нормали в этой точке. Из этих произведений можно составить интегральные суммы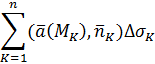
 .
.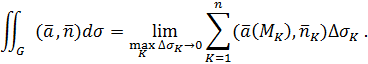
 непрерывно на поверхности
непрерывно на поверхности 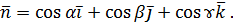

 . Для этого рассмотрим два случая.
. Для этого рассмотрим два случая. на
на  как интеграл от нулевой функции.
как интеграл от нулевой функции. – знакопостоянная функция на поверхности
– знакопостоянная функция на поверхности  на всей поверхности
на всей поверхности  . Обозначим через
. Обозначим через  проекцию на эту плоскость. Тогда, если
проекцию на эту плоскость. Тогда, если 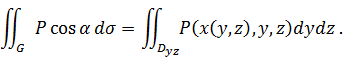
 на
на 

 , если
, если  , если
, если  , если
, если 

 получена в предложении, что каждая из координат вектора нормали
получена в предложении, что каждая из координат вектора нормали  либо знакопостоянна всюду на поверхности
либо знакопостоянна всюду на поверхности 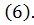
 Пример 3. Найти поток векторного поля
Пример 3. Найти поток векторного поля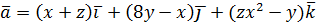
 , на которой
, на которой  ,
, то
то  Кроме того, очевидно, что
Кроме того, очевидно, что  и
и  Поэтому формула
Поэтому формула 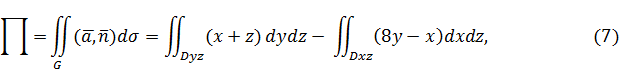
 и
и -
- и
и  соответственно.
соответственно.
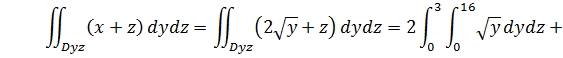
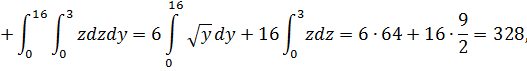
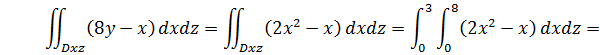
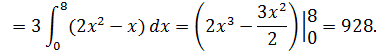
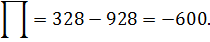
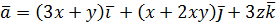
 и
и  Положительным считается направление внешней нормали.
Положительным считается направление внешней нормали. Решение. Так как
Решение. Так как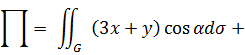
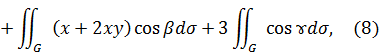
 и
и
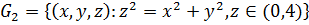
 вектором внешней нормали является вектор
вектором внешней нормали является вектор  а на
а на - вектор
- вектор 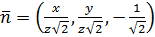

 и
и 


 - проекция поверхностей
- проекция поверхностей 
 на
на 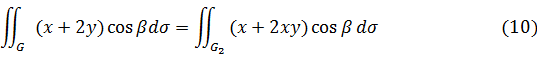
 не является знакопостоянной функцией на всей поверхности
не является знакопостоянной функцией на всей поверхности 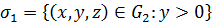 и
и  .
. на
на  и
и  на
на  . Поэтому
. Поэтому  на
на  однозначно проектируются на область
однозначно проектируются на область (см. Рис.6)
(см. Рис.6) следует, что
следует, что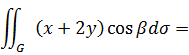
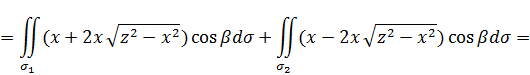
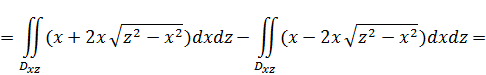
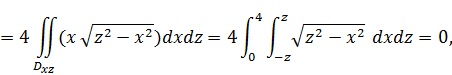
 функции по симметричному отрезку.
функции по симметричному отрезку.
 и
и  . Тогда
. Тогда  на
на  и
и 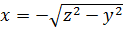 на
на  .
. на
на  на
на  , получаем
, получаем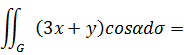

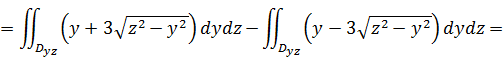

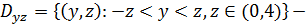
 проекция поверхностей
проекция поверхностей  к повторному интегралу, получаем
к повторному интегралу, получаем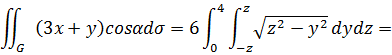
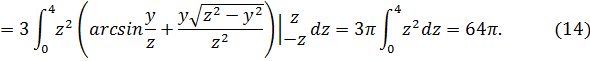
 окончательно имеем
окончательно имеем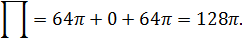
 от скалярного поля
от скалярного поля 
 через поверхность
через поверхность  .
.


