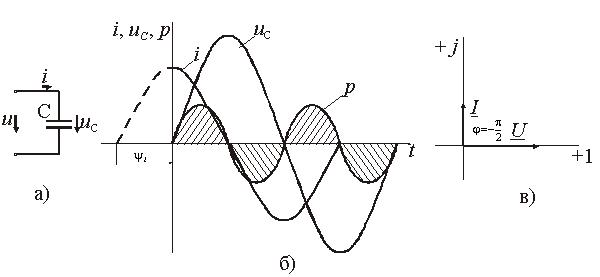
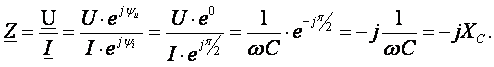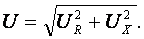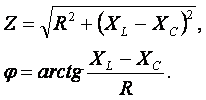Цепь синусоидального тока с идеальным конденсатором.
Конденсатор – элемент электрической цепи, предназначенный для использования его ёмкости. В конденсаторе накапливается энергия электрического поля. Свойство элемента запасать электрический заряд характеризует ёмкость. Этот параметр является коэффициентом пропорциональности между зарядом q и прикладываемым напряжением u q = C·u, где q – выражается в кулонах [Кл], С – в фарадах [Ф], u – в вольтах [B]. При изменении напряжения на конденсаторе изменяется заряд и возникает электрический ток
Идеализированный конденсатор обладает только параметром С. Рассмотрим электрические процессы в цепи с идеальным ёмкостным элементом, рис., а.
Пусть напряжение источника изменяется по закону u = U m·sinω· t, (ψ;u = 0). В цепи возникает ток
Из полученного выражения видно, что начальная фаза тока ψ;i = π/2. Угол сдвига фаз между напряжением и током составляет φ; = ψu – ψ;i = 0 – π/2 = - π/2. Следовательно, синусоида напряжения на емкости отстаёт от синусоиды тока на угол π;/2, рис. 3.6, б, в. На практике, если в электрической цепи напряжение отстаёт по фазе от тока, говорят об ёмкостном характере нагрузки. Амплитуда тока I m = ω· C · U m, действующее значение
Это выражение представляет закон Ома. Величину 1/ ω·C называют ёмкостным сопротивлением конденсатора и измеряют в [Ом]
Ёмкостное сопротивление имеет место только в том случае, когда происходит изменение напряжения на обкладках конденсатора. При постоянном напряжении (f = 0) ёмкостное сопротивление равно бесконечности (т. е. В цепи будет разрыв). Мгновенная мощность ёмкостного элемента
Амплитуда мгновенной мощности равна реактивной мощности Q C = U·I = X C· I 2. Активная мощность (средняя за период) равна нулю, рис., б. С энергетической точки зрения график мгновенной мощности отражает накопление энергии в электрическом поле конденсатора (когда мощность положительная) и возврат её источнику питания (когда мощность отрицательная). Следовательно, ёмкостной элемент является реактивной нагрузкой. Выразим электрические величины в комплексной форме. Напряжение и ток (действующие значения) в цепи имеют вид U = U · ej ·ψu, I = I · ej ·ψi , ψu = 0, ψi = π/2, φ; = - π/2. Комплексное сопротивление цепи
Ёмкостное сопротивление является отрицательным мнимым числом.
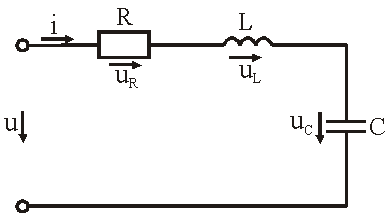
Последовательное соединение активного, индуктивного и ёмкостного элементов. Рассмотрим процессы, происходящие в цепи, содержащей индуктивную катушку с параметрами L, R и конденсатор с параметром С. Схема замещения цепи показана на рисунке.
Для последовательной цепи общим является ток. Согласно второму закону Кирхгофа для мгновенных значений напряжение на входе цепи определяется выражением u = u R + u L + u C. Запишем это уравнение в комплексной форме U = U R + U L + U C. Представим это уравнение векторной диаграммой, рис. 3.8, а. Построение векторной диаграммы начинаем с отложения на комплексной плоскости вектора тока I, который является общим для всех элементов цепи. Причём направление вектора выбираем произвольно. На рис 3.8, а вектор тока I выбран совпадающим с положительным направлением действительной оси. Вектор напряжения на активном сопротивлении U R совпадает по направлению с вектором тока, его называют активной составляющей напряжения, U R = R ∙ I. Вектор напряжения на индуктивности катушки U L = jX L∙ I опережает вектор тока на угол 90°. Вектор напряжения на ёмкости U C = - jX C∙ I отстаёт от вектора тока на угол 90°. Геометрическая сумма трех векторов напряжения даёт вектор напряжения U, приложенного к цепи. Результирующий вектор напряжения U опережает вектор тока I на угол φ;. При построении диаграммы условно принято U L > U C. В построенной диаграмме можно выделить треугольник ОАВ, называемый треугольником напряжений. Сторона треугольника АВ = U Х = U L + U C = j (XL – XC)· I называется реактивной составляющей напряжения. Из треугольника напряжений можно найти модуль напряжения на зажимах в цепи
Заменяя напряжения на элементах произведением тока на соответствующие сопротивления, получаем U = R· I + jX L· I – jX C · I = I ·[ R + j (X L – X C)] = Z · I, где Z – полное комплексное сопротивление цепи, Z = R + j (X L – X C). Из треугольника сопротивлений можно определить модуль полного сопротивления и угол φ;
|


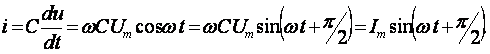
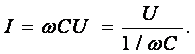
 .
.