Формы представления синусоидальных электрических величин.
Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах. 1). Аналитическая форма представления I = Im ·sin(ω·t + ψi), u = Um ·sin(ω·t + ψu), e = Em ·sin(ω·t + ψe), где I, u, e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени; Im, Um, Em – амплитуды синусоидального тока, напряжения, ЭДС; (ω·t + ψ;) – фазовый угол, фаза; ω; = 2·π/ Т – угловая частота, характеризующая скорость изменения фазы; ψ;i, ψ;u, ψ;e – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение. Графики мгновенных значений тока и напряжения показаны на рис. 2.3 Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψ;u > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψ;i < 0. Алгебраическая величина, равная разности начальных фаз двух синусоид, называется сдвигом фаз φ;. Сдвиг фаз между напряжением и током φ; = ψ;u – ψ;i = ψ;u – (- ψ;i) = ψ;u + ψ;i. Применение аналитической формы для расчёта цепей является громоздкой и неудобной. На практике приходится иметь дело не с мгновенными значениями синусоидальных величин, а с действующими. Все расчёты проводят для действующих значений, в паспортных данных различных электротехнических устройств указаны действующие значения (тока, напряжения), большинство электроизмерительных приборов показывают действующие значения. Действующий ток является эквивалентом постоянного тока, который за одно и то же время выделяет в резисторе такое же количество тепла, как и переменный ток. Действующее значение связано с амплитудным простым соотношением
2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω; = 2 πf. Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.
Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4 3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.
Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис.2.5 Ось абсцисс называют осью действительных чисел и обозначают +1, ось ординат называют осью мнимых чисел и обозначают +j. (В некоторых учебниках ось действительных чисел обозначают Re, а ось мнимых – Im). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах: а). Алгебраической U = U ’+ jU " I = I ’ – jI ", где U ', U ", I ', I " – проекции векторов на оси действительных и мнимых чисел. б). Показательной
где U, I – модули (длины) векторов; е – основание натурального логарифма; в). Тригонометрической U = U ·(cos ψ;u + j sin ψ;u) I = I ·(cos ψ;i – j sin ψ;i). При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера еj ·ψ = cos ψ; + j sin ψ;. Неразветвлённые электрические цепи
|





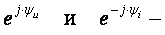 поворотные множители, т. к. умножение на них соответствует повороту векторов относительно положительного направления действительной оси на угол, равный начальной фазе.
поворотные множители, т. к. умножение на них соответствует повороту векторов относительно положительного направления действительной оси на угол, равный начальной фазе.


