Оптимизация с учетом ограничений в форме неравенств

Общая задача нелинейного программирования содержит ограничения в форме неравенств

F(Х) ® min;

G(Х) ≥ 0.

Учет таких ограничений является наиболее сложным. Простейший подход, заключающийся в последовательном решении задачи без учета ограничений с последующей проверкой ограничений и закреплении вышедших за допустимую область переменных на границе, далеко не всегда дает правильное решение.

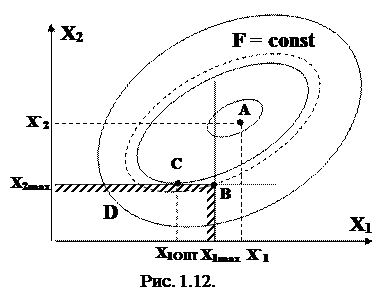
На рис.1.12 показан такой случай F(x) ® min; g₁(x) ≥ 0; g₂(x) ≥ 0.

Решение без учета ограничений определяет точку A(x`<sub>1</sub>,x`₂), в которой нарушены оба ограничения

g₁(x) = x_1max – x₁ < 0;

g₂(x) = x_2max – x₂ < 0;

Закрепление переменных на границе определяет точку В предполагаемого решения, для которой x_1ОПТ = x_1max, x_2ОПТ = x_2max.

Фактически же решение лежит в точке C. В этой точке только x_2ОПТ лежит на границе и ограничение g₂(x) называют активным. Переменная x_1ОПТ < x_1max, и ограничение g₁(x) называют пассивным.

Таким образом, при решении могут возникнуть самые разные ситуации, в которых надо определять тип ограничений (активные или пассивные). При учете активных ограничений нужно использовать проекции градиента, если антиградиент выводит за допустимую область и т.п.

Поэтому для учета ограничений в форме неравенств существует много методов. Большинство основано на идее проектирования градиента и называются проективными. В последнее время начинают использовать методы, основанные на линеаризации, т.е. замене нелинейностей в исходной точке Х⁽⁰⁾ разложением в ряд Тейлора с учетом первых двух членов разложения, линеаризации задачи и поиска минимума симплекс- методом.

Критерием окончания такого итерационного процесса является небольшая разница между значениями, полученными на смежных итерациях.

Наиболее простой метод учета ограничений – метод штрафных функций. Здесь допускается любое значение неизвестных, но при выходе за допустимую область к F(X) добавляется штрафная функция. Величина штрафа зависит от степени нарушения ограничений.

Формируемая функция имеет вид ,

где ;

.

На рис. 1.13 показана оптимизация для функции с одной переменной:

f(x)®min;

g₁(x) = x _max – x ³ 0;

g₂(x) = x – x _max ³ 0;

 

Решение по методу всегда лежит за допустимой областью, но вблизи границы.

Жесткость ограничения зависит от величины коэффициента штрафа k_Ш. Сочетание метода штрафных функций с методами нулевого порядка позволяет строить надежные алгоритмы решения общей задачи нелинейного программирования.